はじめに
最近はコロナコロナでなんだか世紀末みたいになってますね。ふとPythonでこのコロナの感染拡大について分析できないかなあ、と思いたち本稿を執筆しました。あくまでツールとして分析手法を提示するだけの記事のため、この記事が何かを結論付けることはありませんのでご了承ください。この記事を呼んで感染症分析やグラフ理論について興味を持っていただけたら幸いです。是非本稿でPythonのnetworkxを動かしてみて下さい☆
目次
- SIRモデル
- 接触ネットワーク
- Watts-Strogatzモデル
SIRモデル
SIRとはSusceptible Infectious Removedの略で、$S$(健康な人)、$I$(病気を移す可能性のある感染者)、$R$(病気を移す可能性のない感染者)のように人を3つのグループに分けて感染動態を表現する方法です。まず実際に式を見てみましょう。
S + I → 2I
I → R
これがSIRモデルとなります。化学反応式と同じイメージをして下さい。健康な人 $S$ は感染者 $I$ と会うことである一定の確率で感染者 $I$ になります。これが一番目の式です。また、感染者 $I$ は完治したり死亡したり隔離されるなどの様々な要因によって病気を移す可能性のない感染者 $R$ となります。これが二番目の式です。(勘のいい読者はお気づきでしょうが再感染を考慮していません)
次にここに時間発展の概念を与えます。時間 $t$ における $S$ を $S(t)$ 、$I$ を $I(t)$ 、$R$ を $R(t)$ とします。上の式ですが、化学反応と同様に $S$ は $S$ とIの積に比例して定率で $I$ に移行し、$I$ は定率で $R$ に移行するという仮定となっております。つまり、これを連続力学系で表すと
\frac{dS}{dt}(t)=-βS(t)I(t)
\frac{dI}{dt}(t)=βS(t)I(t)-γI(t)
\frac{dR}{dt}(t)=γI(t)
となります。ここで $β$ は感染率、$γ$ は回復や隔離をまとめて表現した定数となります。以上がSIRモデルの説明となります。ここまでの内容を実装しました。定数を変えていじってみて下さい。
import numpy as np
from scipy.integrate import odeint
def sir_graph(t_max, dt, beta, gamma, S_0, I_0, R_0):
"""
t_max: 最大経過時間
dt: 時間の微小変化値
S_0, I_0, R_0: S, I, Rの初期値
"""
def SIR_EQ(SI, t, beta, gamma):
# 時間経過をシミュレーションする関数
# odeintの都合でSI[0] = S, SI[1] = S となるようにする
return [-beta*SI[0]*SI[1], beta*SI[0]*SI[1] - gamma*SI[1], gamma*SI[1]]
ini_state = [S_0, I_0, R_0]
times =np.arange(0 ,t_max, dt)
# SIRmodelの経時変化
result = odeint(SIR_EQ, ini_state, times, (beta, gamma))
return times, result
# 実行と可視化
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(*sir_graph(t_max=120, dt=0.01, beta=0.001, gamma=0.45, S_0=499, I_0=1, R_0=0))
plt.legend(['Susceptible','Infectious', 'Removed'])
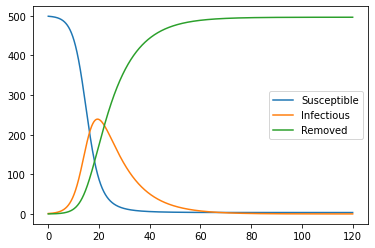
例 500人の中で1人の感染者からβ=0.001、γ=0.1で感染拡大
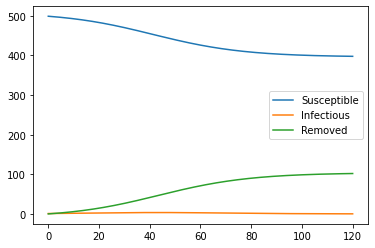
例 500人の中で1人の感染者からβ=0.001、γ=0.45で感染収束
Rの最終的な値が総感染者数と考えると、保因者の隔離の重要性がわかりますね。
接触ネットワーク
もう一度SIRモデルの仮定を考えて見ましょう
- $S$ : 感染する可能性がある人。基礎疾患の有無などは無視
- $I$ : 人に感染させるポテンシャルのある人。潜伏期などは無視
- $R$ : $I$ から移行する感染することも感染させることもない人。回復・隔離・死亡などが含まれる
- $S$ と $I$は 化学反応のようにランダム接触する
以上がSIRモデルの仮定となります。しかし、実社会では地理的にも人間関係的にも接触はランダムではありません。この仮定には無理があります。ここで接触ネットワークの考え方を導入します。
まず人をノード (まる○) 、接触をエッジ (線ー)と表すことにします。下の図を見て下さい。
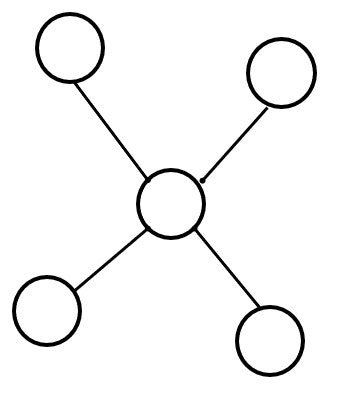
人と人の接触をこのようなグラフで表し、感染アルゴリズムを考えていきます。
まず、この中からランダムに人 (ノード) を一つ選択します。今回真ん中の人 (ノード) を選択したとします。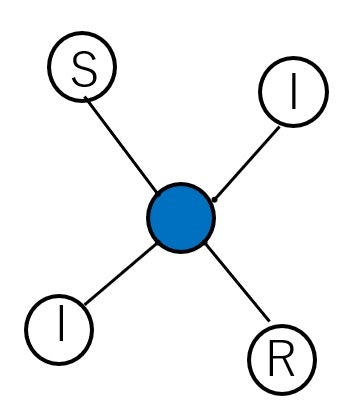
$ $選ばれた人 (ノード) が $S$ の場合: このノードが確率 $βnIdt$ で $I$ に変えます。この $n$ は隣接する $I$ の数で今回の例では $n=2$ となります。$dt$ については時間ステップをかけていると考えて下さい。
選ばれた人 (ノード) が $I$ の場合: このノードが確立 $γdt$ で $R$ に変えます。
選ばれた人 (ノード) が $R$ の場合: 何もしない。
以上のアルゴリズムを繰り返します。このようにネットワークにおける感染症をシミュレーションします。(追記: ノード一つあたりから伸びるエッジの本数を平均次数と言います。本稿では $k$ と表します)
Watts-Strogatzモデル
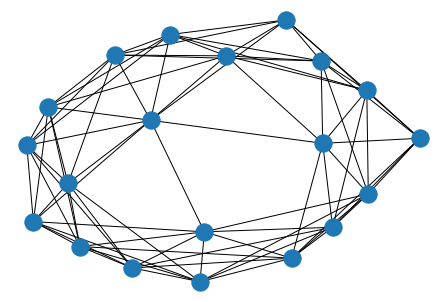
では、どのようなネットワークの上でこのアルゴリズムを走らせれば良いのでしょうか?これはWatts-Strogatzモデルを使うのが良いとされています。あるノードから最近傍の $K$ (平均次数) 個のノードと結び付けます。ノード数 $n=20$ 、平均次数 $k=8$ の場合下の図の様になります。
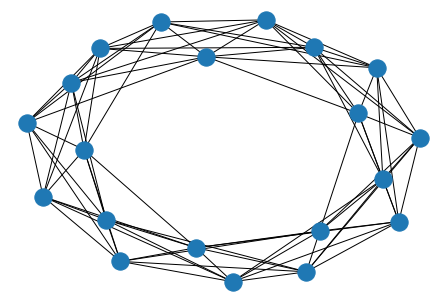
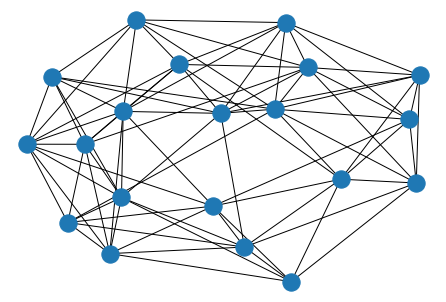
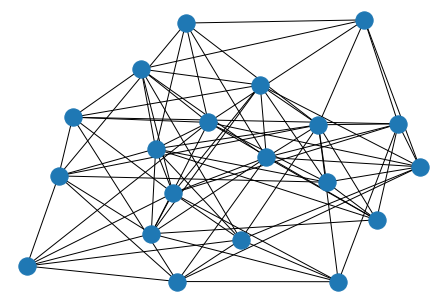
ここから確率 $p$ でネットワークをランダムに組み替えます。$p=0.01,0.1,1$ で組み替えてみましょう。
$p=0$ が規則正しいレギュラーなネットワークで、$p=1$ が完全にランダムなネットワークとなります。では、これらの $L$ (平均ノード距離)、$C$ (クラスター係数) を求めてみましょう。$L$ (平均ノード距離) とは何人たどれば任意の人に会えるかみたいなイメージです (日本だと友達7人たどれば有名人に会えるなんていいますよね)。$C$ (クラスター係数) は友達の友達が友達である確率のようなものです。自分とエッジで結ばれているノードとエッジで結ばれているノードが自分と直接エッジで繋がっている確率というものが $C$ (クラスター係数) です。上の例だと次のようになります。
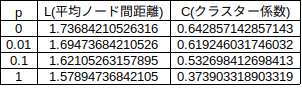
ノード数 $n=20$ なのであまり違いがわかりませんね。では、$n=1000$ でやってみましょう。結果は下のようになります。
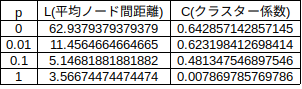
確率 $p$ が大きくなるに連れてLとCが減少することが分かりますね。面白いことに $p=0.1,0.01$ では $C$ の値をある程度の大きさに保ったまま $L$ が大きく減少していますね。これらを Small World と呼んだりします。次にこれらのネットワークからSIRモデルを考えてみましょう。以下にこの章で使ったコードを記載します。
import networkx as nx
import matplotlib.pyplot as plt
G = nx.watts_strogatz_graph(100, 8, 1) # watts_strogatzモデルの定義 (ノード数, 平均次数, 組み換え確率)
nx.draw(G) # 組み換え確率が1 → nx.draw_random(G)
plt.show()
print(nx.info(G))
print("平均ノード間距離:", nx.average_shortest_path_length(G))
print("クラスター係数:", nx.average_clustering(G))
SIR + Watts-Strogatzモデル
それでは、最後にSIRモデルとWatts-Strogatzモデルを実際に合わせてみましょう。下の様に実装します。
!pip install -q ndlib
!pip install -q bokeh
import networkx as nx
import ndlib.models.epidemics as ep
import ndlib.models.ModelConfig as mc
from bokeh.io import output_notebook, show
from ndlib.viz.bokeh.DiffusionTrend import DiffusionTrend
import matplotlib.pyplot as plt
G = nx.watts_strogatz_graph(1000,8,0.01) # watts_strogatzモデルの定義 (ノード数, 平均次数, 組み換え確率)
nx.draw(G)
plt.show()
print(nx.info(G))
print("平均ノード間距離:", nx.average_shortest_path_length(G))
print("クラスター係数:", nx.average_clustering(G))
model = ep.SIRModel(G)
config = mc.Configuration()
config.add_model_parameter('beta',0.1)
config.add_model_parameter('gamma',0.1)
config.add_model_parameter('percentage_infected',0.001)
model.set_initial_status(config)
iterations = model.iteration_bunch(75)
trends = model.build_trends(iterations)
output_notebook()
viz = DiffusionTrend(model,trends)
p = viz.plot(width=400, height=400)
show(p)
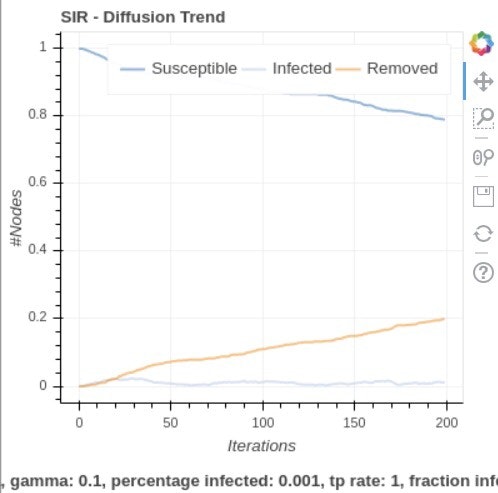
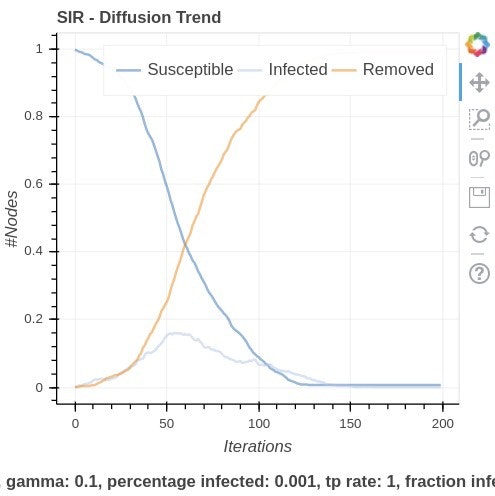
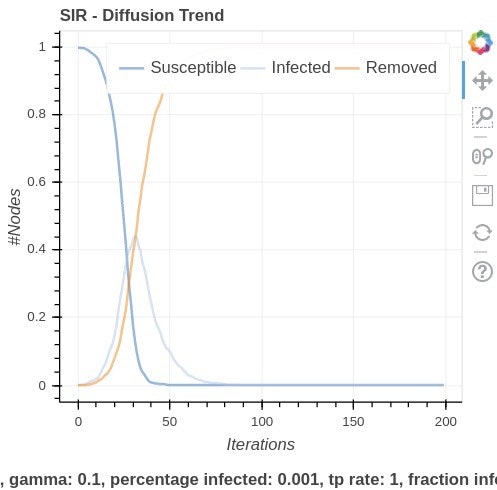
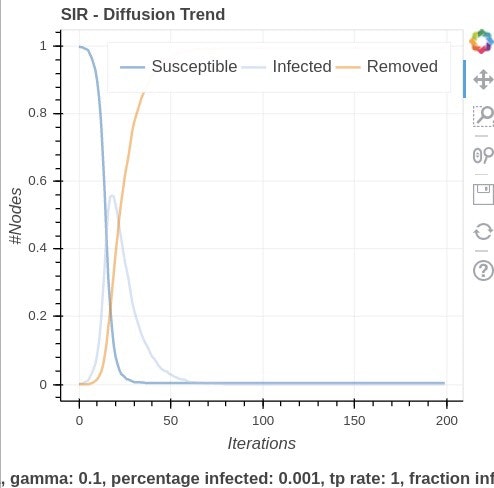
ここでの percentage_infected というのは集団での最初の感染者の割合です。ここでは1000人の集団で1人の感染者からの増加を考えたいので、percentage_infected = 0.001 として計算します。$β=0.1$, $γ=0.1$, $n=1000$, $k=8$ で計算してみましょう。上から$p=0, 0.01, 0.1 , 1$ での出力結果となります。
ランダム性が増すにつれて感染爆発のタイミングが早く急激に起こることが改めて分かりますね。若者のライブやクラブなどはランダム性の増加につながるので辞めましょうね(こじつけ)
皆さんもこのコードのパラメータをいじって分析してみてください。この分析手法で医学的な観点で分析した記事についてはまた今度出すかもしれません、、
参考資料
2010年、日本人工知能学会 湯浅友幸・白山晋、感染症流行予測におけるネットワーク構造の影響分析
山下雄史のyoutube研究室SIRモデルとネットワーク理論