はじめに
科学計算で用いられるGaussianですが、コマンドの引数ではなく、インプットファイルを作成してそれを読み込ませることで実行するため、自動化や系統処理に少しだけテクニックが必要になります。
今回は第1回ということで、「酸素の結合距離とエネルギー」をグラフ化するスクリプトをPythonを用いて書いてみます。
Gaussianを使われる方の中にはPythonをあまり知らない人もいると思われるので、今回はそちらのも合わせてしようと思います。
どうぞよろしくお願いします。
Gaussian インプットファイルの作り方
以下に例を示します。
%nprocshared=4
%mem=4GB
%chk=test.chk
# UHF/6-31G* SP
O2/UHF/6-31G*/ calc.
0 3
O -0.5 0.0 0.0
O 0.5 0.0 0.0
はじめの3行を見てみます。
%nprocshared=4
%mem=4GB
%chk=test.chk
% で始まるこれらの行には計算における設定をすることができます。1行目は4コアで行うこと、2行目はメモリを4GB使用すること、3行目はチェックポイントファイルをこのようなファイル名で生成すること、をそれぞれ指定しています。
# UHF/6-31G* SP
# で始めるこの行は、計算手法を設定します。ここでは詳しく述べませんが、計算手法を__UHF__、基底関数を__6-31G*__、を用いて一点計算を行うよう指示します。一点計算は与えられた原子の位置を固定してそのエネルギーを計算します。構造を最適化する際には__opt__を指定します。
O2/UHF/6-31G*/ calc.
この行はコメント行です。プログラム自体には関係ありませんが、計算結果に出力されるので、わかりやすいコメントを心がけましょう。
0 3
O -0.5 0.0 0.0
O 0.5 0.0 0.0
ここで原子の情報を入力します。初めの1行は、イオン価数、多重項状態を指定します。酸素分子はイオンではなく、三重項ですのでこのようになります。
また、それ以降に原子の座標を入力していきます。入力の仕方には、今回のようにx, y, zの座標を入力するカーテシアン座標系と、相対位置を入れていくz-matrixという方法があります。前者の方は座標が直感的にわかりやすい、後者の方は置換基などを挿入しやすいなどの利点があります。今回はわかりやすくするためxyz座標で入力しています。
また、今回変更していきたい部分はこのO原子のx座標です。
Pythonで書いていこう
実際に書いていきます。
データ作成部分
Pythonには、任意の数字や文字列を文字列に代入するformat記法があります。今回は__0.6 ~ 20.0 Å__の間で、__0.1 Å__刻みで計算していこうと思います。
distance = 0.6 # ここで初期の原子間距離を設定します。
while distance < 20.0: # 原子間距離が20になるまで実行し続けます
input_file = """
%nprocshared=4
%mem=4GB
%chk=test.chk
# UHF/6-31G* SP
O2/UHF/6-31G*/ calc.
0 3
O -{} 0.0 0.0
O {} 0.0 0.0
""".format(distance/2, distance/2) # ここでインプットファイルを作成します。多数行文字列の間はインデントを無視します。
# さらに、format記法により{}の部分に数値を代入します。
with open("input.gjf", mode="w", encoding="utf-8") as f: # input.gjfというファイルを書き込みモードで開きます
f.write(input_file) # 開いたファイルに先ほどの文字列を書き込みます。
distance += 0.1 # 0.1だけ結合距離を増やします
これで、核間距離を変えながらインプットファイルを作成することができました。
ファイル実行
通常のGaussianはコマンドラインから実行しますので、Pythonでも同様にします。subprocessモジュールによって、コマンドラインをPythonから実行することができます。
import subprocess
subprocess.call("g16 input.gjf", shell=True)
これで、自動的に計算され、input.log というログファイルが生成されます。
得られたデータの読み取り
ログファイルから、必要なデータ(今回は全エネルギー)をPythonで取り出しましょう。ログファイルの以下のような部分です。
SCF Done: E(UHF) = -198.672786803 A.U. after 1 cycles
ここで注意しなけらばならないことが、この出力が1回のみではないときがあるということです。収束しなかった場合は再度収束計算が行われますが、そのときのデータもこのように出力されることがあります。そのため、一番最後の最新のデータが真の計算結果であるため、その都度更新してあげます。
また、文字列の処理の仕方ですが、
- __SCF Done__の文字列があれば使用する
- 文字列を__A.U.__の前までに切り取る
- __SCF Done: E(UHF) =__を切り取る
- 前後のスペースを取り除く
- 小数値へ変換する
このような手順で行います。
with open("input.log", mode="r", encoding="utf-8") as f:
for line in f.readlines():
if "SCF Done" in line: # 1
txt = line[:line.index("A.U.")] # 2
txt = txt.replace("SCF Done: E(UHF) =", "") # 3
txt = txt.strip() # 4
energy = float(txt) # 5
これで読み込みができました。
あとは、核間距離と得られたエネルギーをそれぞれリストへ収納し、グラフにプロットして完成です。
最終的なソースコードがこちら。
import subprocess
import matplotlib.pyplot as plt
distance = 0.6 # ここで初期の原子間距離を設定します。
X = [] # グラフ用のリストです
Y = [] # グラフ用のリストです
while distance < 20.0: # 原子間距離が20になるまで実行し続けます
input_file = """
%nprocshared=4
%mem=4GB
%chk=test.chk
# UHF/6-31G* SP
O2/UHF/6-31G*/ calc.
0 3
O -{} 0.0 0.0
O {} 0.0 0.0
""".format(distance/2, distance/2) # ここでインプットファイルを作成します。多数行文字列の間はインデントを無視します。
# さらに、format記法により{}の部分に数値を代入します。
with open("input.gjf", mode="w", encoding="utf-8") as f: # input.gjfというファイルを書き込みモードで開きます
f.write(input_file) # 開いたファイルに先ほどの文字列を書き込みます。
subprocess.call("g16 input.gjf", shell=True) # 計算の実行
with open("input.log", mode="r", encoding="utf-8") as f:
for line in f.readlines():
if "SCF Done" in line: # 1
txt = line[:line.index("A.U.")] # 2
txt = txt.replace("SCF Done: E(UHF) =", "") # 3
txt = txt.strip() # 4
energy = float(txt) # 5
X.append(distance) # 核間距離をXに入れます
Y.append(energy) # 得られたエネルギーをYに入れます
# break
distance += 0.1 # 0.1だけ結合距離を増やします
plt.plot(X, Y)
plt.title("O2 Energies")
plt.xlabel("Distance (angstrom)")
plt.ylabel("Energy (hartree)")
plt.savefig("graph.png")
plt.show()
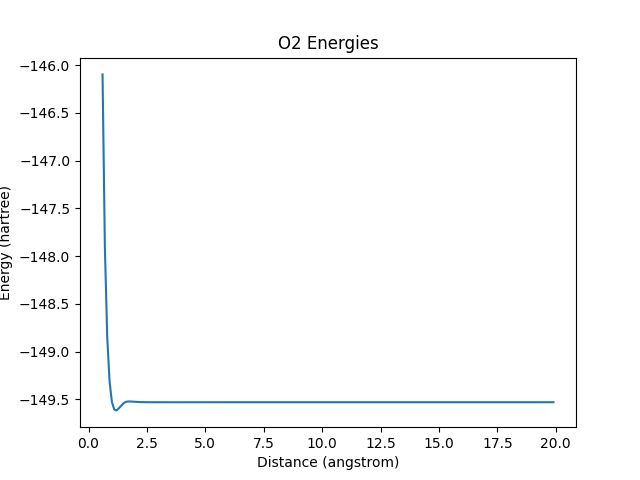
計算してみた!
最後に
Pythonは少ない分量で簡潔にプログラムを書くことができます。今回のような、「手動でやってもいいけどめんどくさいな...」なんて時にサクッとコードが書けると時短にもなりますし、空いた時間でごちうさを見ることができますよね。
皆さんもぜひ、Pythonを使って効率的にGaussianを利用してくださいね!