Disclaimer
まず初めに本稿ではコロナウイルスによる死者数の予測についてのデータを示していますが、これは現在までウィルスにより亡くなられた方、また現在もウィルスによる肺炎などの症状で苦しまれている方を貶めるものではもちろんありません。また、この予測についてはあくまで現時点でのデータから科学的に(=ある一定の手法に則ったやり方で)導かれる結果とそれに対する私の個人的な考察であり、政治的・宗教的その他の意図を持ったものでもありません。あくまで本稿では**「公開されているデータからどのような予測があり得るのか?」について、その手法の1つを再現可能な形で示そうとするもの**です。ですので、もし本稿の内容に興味を持たれた方は私の考察を鵜呑みにせず、是非ご自分で色々と分析してみていただければと思います。
また、ここで述べる意見については私個人の意見であり、本稿での間違いは私に帰属し、所属する組織等とは関係ありません。
本稿を書くに至った動機
率直に言えば、これは私の個人的な**「現在世界で何が起こっているのかを実際に自分の手を動かすことで知りたい」**という試みです。日々コロナウイルスに関する新たな感染者や、コロナショックにより世界経済がとんでもないことになっている、というニュースが報告されていますが、その時々のスナップショットの情報だけでは数字の大小または比較といった判断しかできません。しかし重要なのは、それが今後どういう結果になるのか?、そしてそのような事態に対し我々はどう備えるべきか?、といった事だと思います。
その上で問題になるのは、感染症の感染拡大初期では指数関数的に感染者数が増大しますが(ロジスティック曲線と呼ばれています)、人間はこのような非線形的な増加を上手く認識できない、という事です。
専門家も含めて指数関数的な増加関数を人間は上手く認識できない、ということを近い将来に思い知ることになるだろう。
— Kazuki Fujisawa (@kazu_fujisawa) February 13, 2020
これはある日を境に突然爆発的に感染者数が増加していった、という最近のニュースからも実感できるかもしれません。また、同じようなことは成長戦略の文脈においても言われていますが、これは成長という変数が増殖してゆく過程と考えれば同じものとして捉えることができます。
- イーロン・マスクを成功に導いた「ドミノ戦略」を知れば、「あなたがいつまでも成功できない理由」がわかる
https://www.lifehacker.jp/2016/07/160704domino_strategy.html
このように非線形を認識するのが苦手な我々(というか私)ですが、線形ならなんとか認識できるかと思います。幸い、このような増殖過程初期はlogを取ることで線形近似できることが分かっています(次節)。そこで、このような線形近似というめちゃくちゃ基礎的な手法を使い、モデル化と予測を通じて何とか今世の中で起こっていることを理解したいと思い、自分で手を動かしながらデータ分析してみたのが本稿になります。
理論的背景
上でも述べましたが、**ウィルス、バクテリア、人口などの増加の最も基礎的なモデルとして使われるのがロジスティック曲線(関数)**です。
f(x) = \frac{L}{1+e^{-k(x-x0)}}
例えばロジスティック関数をY軸がlinearとlogでそれぞれプロットし、最初の800サンプルのデータについて線形近似してみると以下のようになります(オレンジの線が近似。k,L,x0のパラメータの値は適当です):
import numpy as np
import matplotlib.pyplot as plt
k = 1; L = 1; x0 = 7.5
x = np.arange(0,15,0.01)
y = [L / (1 + np.exp(-k*(x-x0))) for x in x]
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x[0:500],np.log(y[0:500]))
fit_y = [np.exp(slope*d+intercept) for d in x[0:800]]
fit_x = x[0:800]
fig,axes=plt.subplots(1,2,figsize=(12,4))
axes[0].plot(x, y)
axes[0].set_title('Logistic function (linear plot)')
axes[0].set_xlabel('X')
axes[0].set_ylabel('Y')
axes[1].plot(x, np.log(y))
axes[1].plot(fit_x, np.log(fit_y))
axes[1].set_title('Logistic function (lin-log plot)')
axes[1].set_xlabel('X')
axes[1].set_ylabel('log(Y)')
plt.legend(['Logistic', 'Logistic fit'])
plt.savefig('logistic.png', dpi=400, bbox_inches='tight')
このプロットからは、logでの線形近似は初めの部分しか上手くフィットせず、実際の直線(青色)は次第に直線から離れていく、ということが見て取れますが、これは感染症の場合(すなわちX軸を時間、Y軸を被害者数と見る場合)で言えば、logでの線形近似から実際のデータが離れて出している傾向が見えれば、感染の初期フェーズは脱出しつつある、という事と解釈できます。
しかし、重要なのはその後です。 右側のプロットで初期フェーズから抜け出そうとしているのは、大体x=6あたりですが、それは左側のプロットではどのような段階でしょうか?そう、今から感染者数や死亡者数が爆発的に増大する手前なのです。つまり、線形近似との乖離傾向が見られ出したら、感染は中期フェーズに入り、感染者数・死亡者数の急激な増大に備えなければいけないフェーズに入るのだ、と解釈できるかと思います。
以上のことを念頭に、それでは実際のデータを見てみましょう。
データ収集
データはいくつかのデータソースが考えられますが、今回はWorldometerというサイトからデータを自分で集計しました(と言ってもちまちま手動で数字を抜き出しただけです)。集計方法は、各国の感染データにおいて、初めてコロナウイルスによる死亡者が出た日を1日目とし、それ以降の累積値をカウントしたものをフィッティング用データとしました。フィッティングは最初5日間を除き、6日目以降についてフィッティングを行いました。対象国は現在感染が深刻な状況となっている欧米諸国を中心とし、中国は対象としませんでした。日本については後述しています。
私が集めたデータはここからダウンロード出来ます(3月23日時点まで)。
Kaggleにも24時間毎にアップデートされているCOVID-19のデータがありますが、今回は使いませんでした。
- Worldometer -- COVID-19 CORONAVIRUS PANDEMIC
https://www.worldometers.info/coronavirus/#countries - Kaggle -- COVID-19 Complete Dataset (Updated every 24hrs)
https://www.kaggle.com/imdevskp/corona-virus-report/data
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
import pandas as pd
# データCSV(自作)
corona_df = pd.read_csv('data.csv', index_col=0)
corona_df.head(10)
| Days since the first confirmed death | Italy | Spain | France | UK | US | Iran | Germany | South Korea | Switzerland | Netherlands |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.0 | 1.0 | 1 | 1.0 | 1.0 | 2.0 | 2.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2.0 | 2.0 | 1 | 2.0 | 1.0 | 2.0 | 2.0 | 2.0 | 1.0 | 1.0 |
| 2 | 3.0 | 3.0 | 1 | 2.0 | 6.0 | 4.0 | 3.0 | 2.0 | 1.0 | 3.0 |
| 3 | 7.0 | 8.0 | 1 | 3.0 | 9.0 | 6.0 | 6.0 | 6.0 | 2.0 | 4.0 |
| 4 | 11.0 | 10.0 | 1 | 5.0 | 11.0 | 8.0 | 8.0 | 8.0 | 2.0 | 4.0 |
| 5 | 12.0 | 17.0 | 1 | 6.0 | 12.0 | 12.0 | 9.0 | 11.0 | 3.0 | 5.0 |
| 6 | 17.0 | 30.0 | 1 | 8.0 | 15.0 | 16.0 | 13.0 | 12.0 | 4.0 | 5.0 |
| 7 | 21.0 | 36.0 | 1 | 10.0 | 19.0 | 19.0 | 17.0 | 13.0 | 7.0 | 10.0 |
| 8 | 29.0 | 55.0 | 1 | 11.0 | 22.0 | 26.0 | 26.0 | 16.0 | 11.0 | 12.0 |
| 9 | 41.0 | 86.0 | 1 | 21.0 | 26.0 | 34.0 | 28.0 | 17.0 | 13.0 | 20.0 |
線形近似する
それでは線形近似を行っていきます。statsmodelsライブラリとかもありますが、今回はscipyのライブラリに入っている線形回帰を行う関数linregressを使います。
countries = corona_df.columns
for country in countries:
y = corona_df[country].dropna().values[6:]
ylog = np.log(y)
days = len(y)
x = np.arange(0,days,1,'int')
# 線形近似する。日数とlog(死亡者数)でフィッティング
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x,ylog)
doubling = np.log(2)/slope
print(f'{country}: doubling {doubling:.2} days / R^2: {r_value**2:.2}')
以下が各国のデータをフィッティングした結果になります。doublingは倍加時間、すなわち死亡者数が2倍になるのに何日かかるのかを表す値で、R^2はフィッティングの良さを表す決定係数(寄与率)$R^2$になります。
Italy: doubling 2.7 days / R^2: 0.98
Spain: doubling 2.2 days / R^2: 0.99
France : doubling 2.8 days / R^2: 0.99
UK: doubling 2.1 days / R^2: 0.98
US: doubling 3.4 days / R^2: 0.99
Iran: doubling 3.9 days / R^2: 0.99
Germany: doubling 2.4 days / R^2: 0.98
South Korea: doubling 8.7 days / R^2: 0.92
Switzerland: doubling 2.6 days / R^2: 0.99
Netherlands: doubling 2.1 days / R^2: 0.99
韓国を除くいずれの国のデータにしてもフィッティングは$R^2>0.98$と非常に高いフィッティングを見せています(個人的には仕事でこんな高いフィッティングの値は見たことがありません)。モデル化がワークしていると解釈してよいかと思います。
ここで気になるのは倍加時間です。韓国では約9日で死亡者数が倍になるのに対し、ヨーロッパ諸国では2,3日で倍です。これは10日で16倍というようなペースですから、どんな対策を取るにしろあまりにも早すぎると思います。
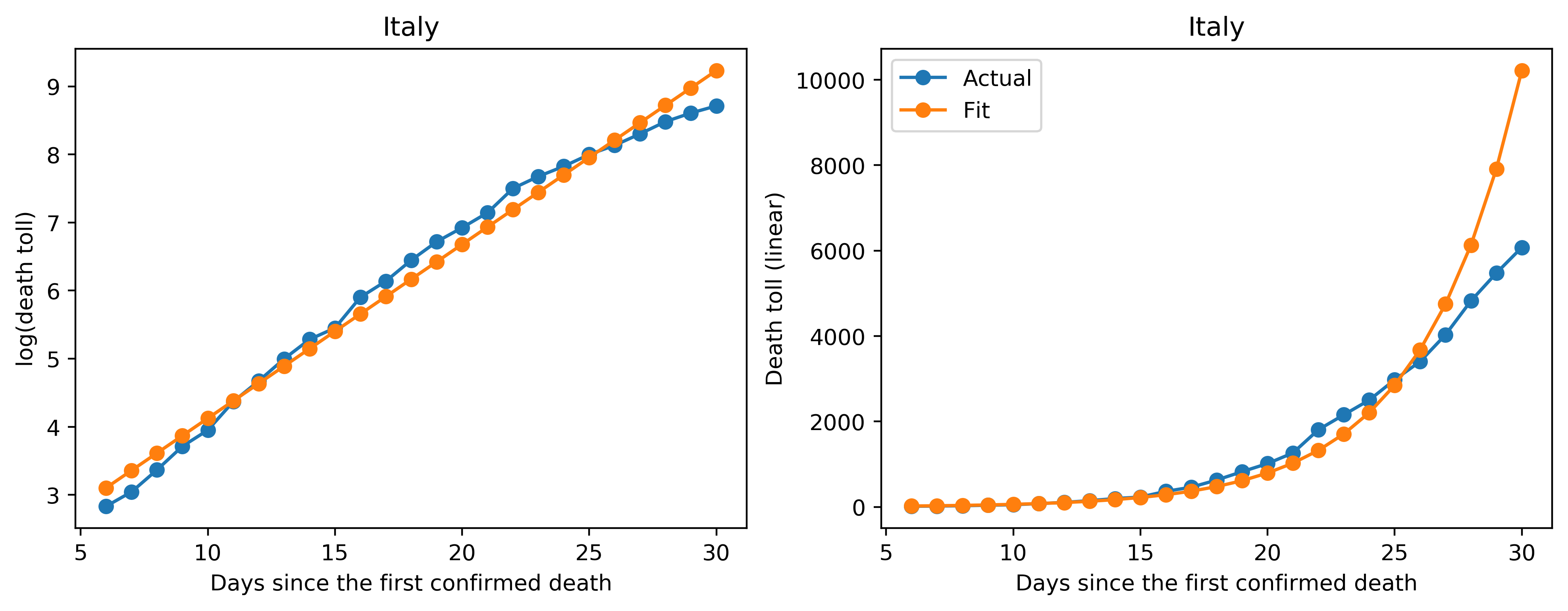
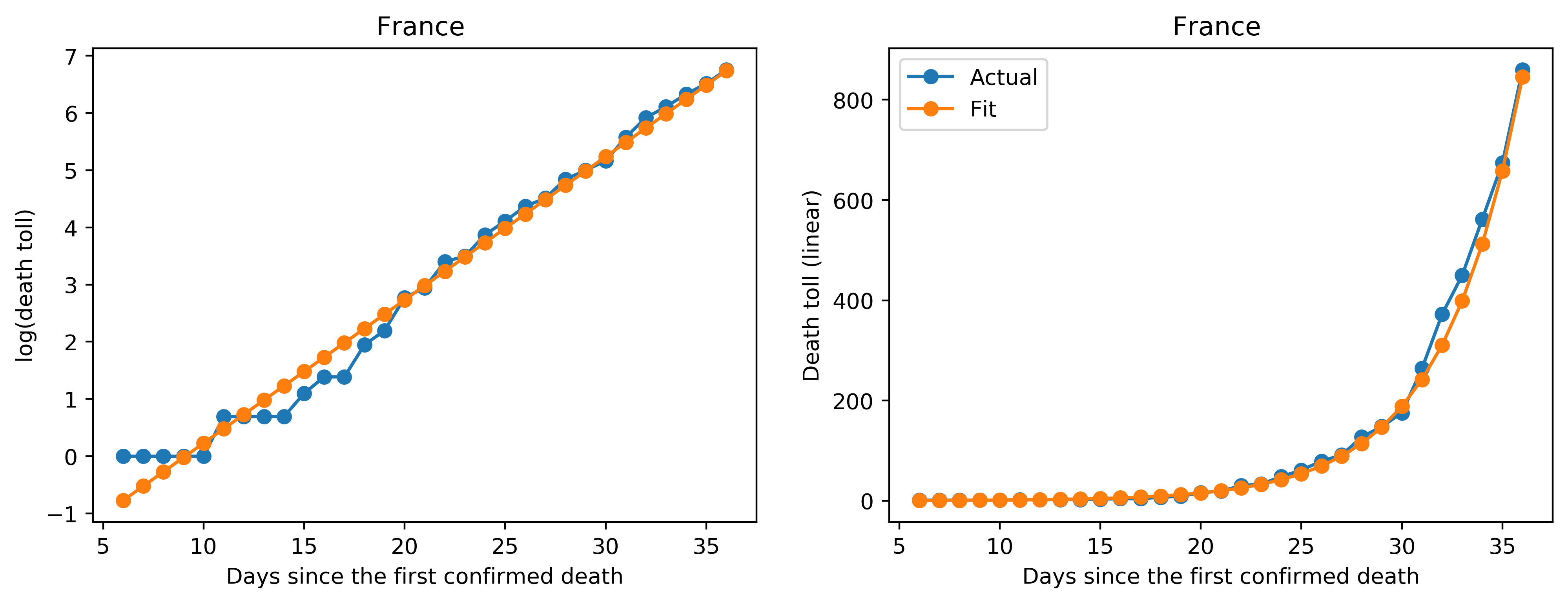
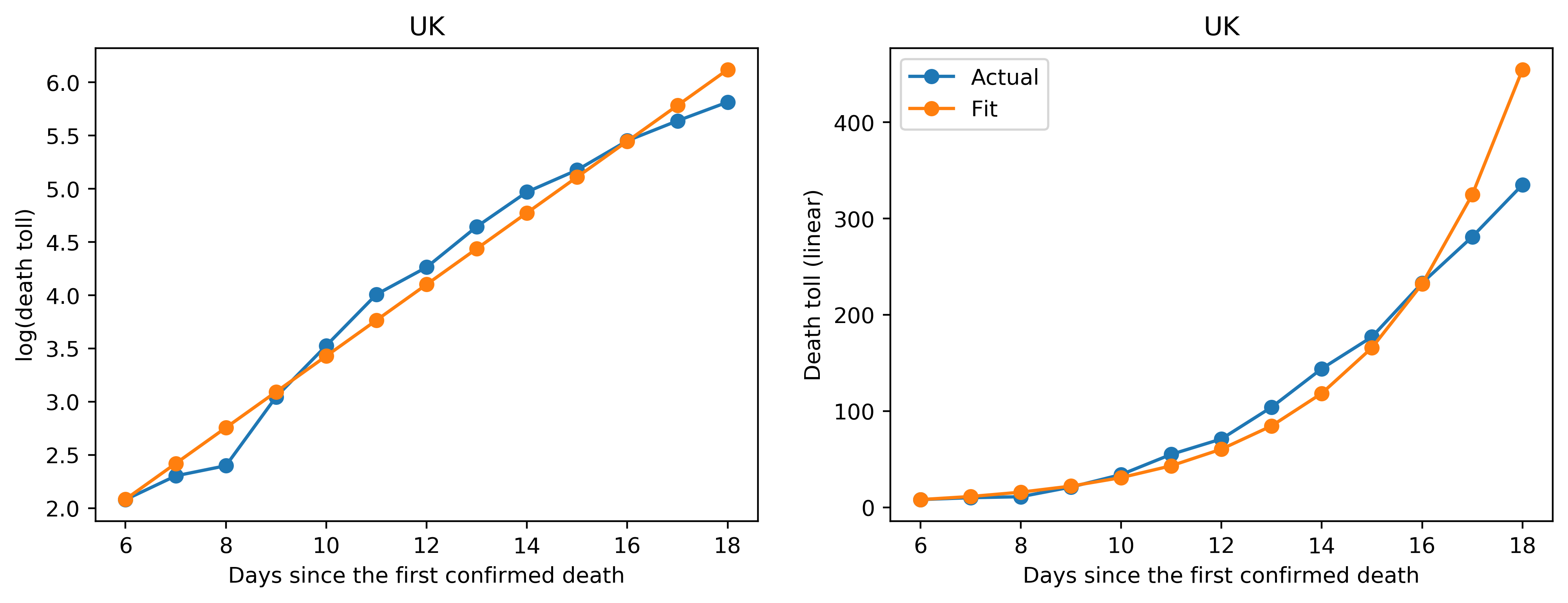
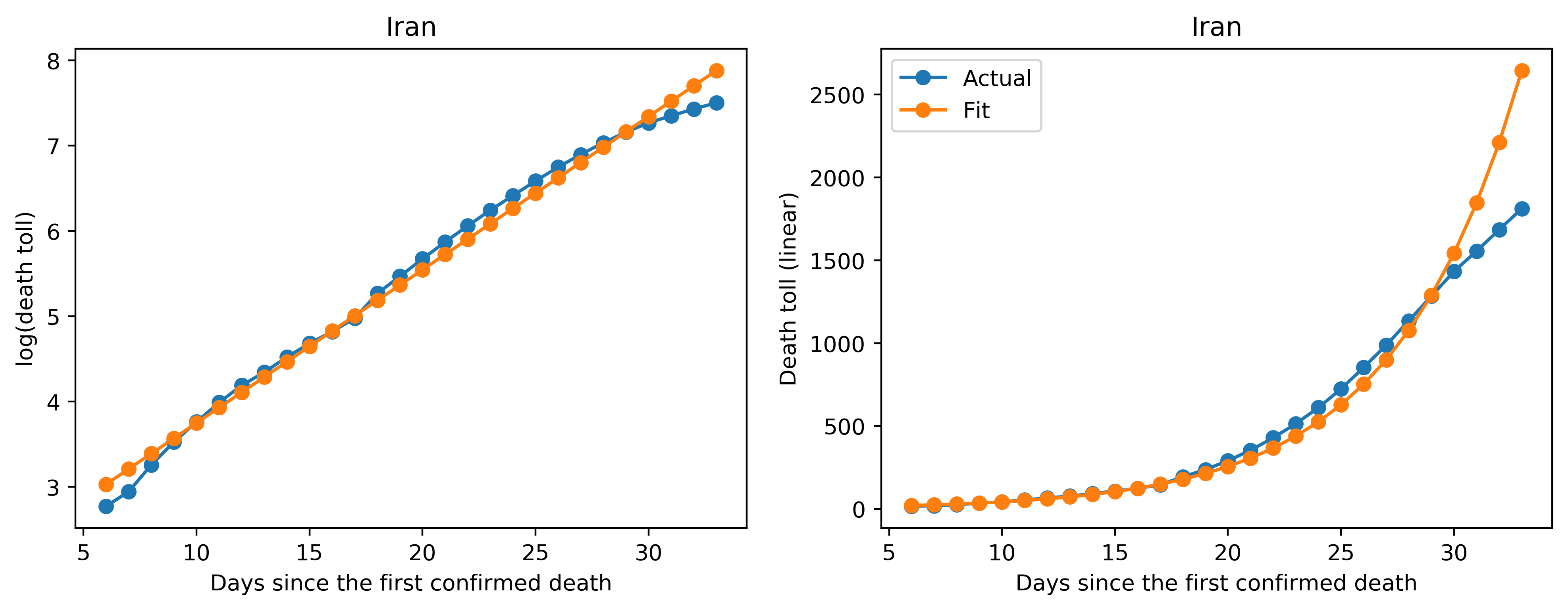
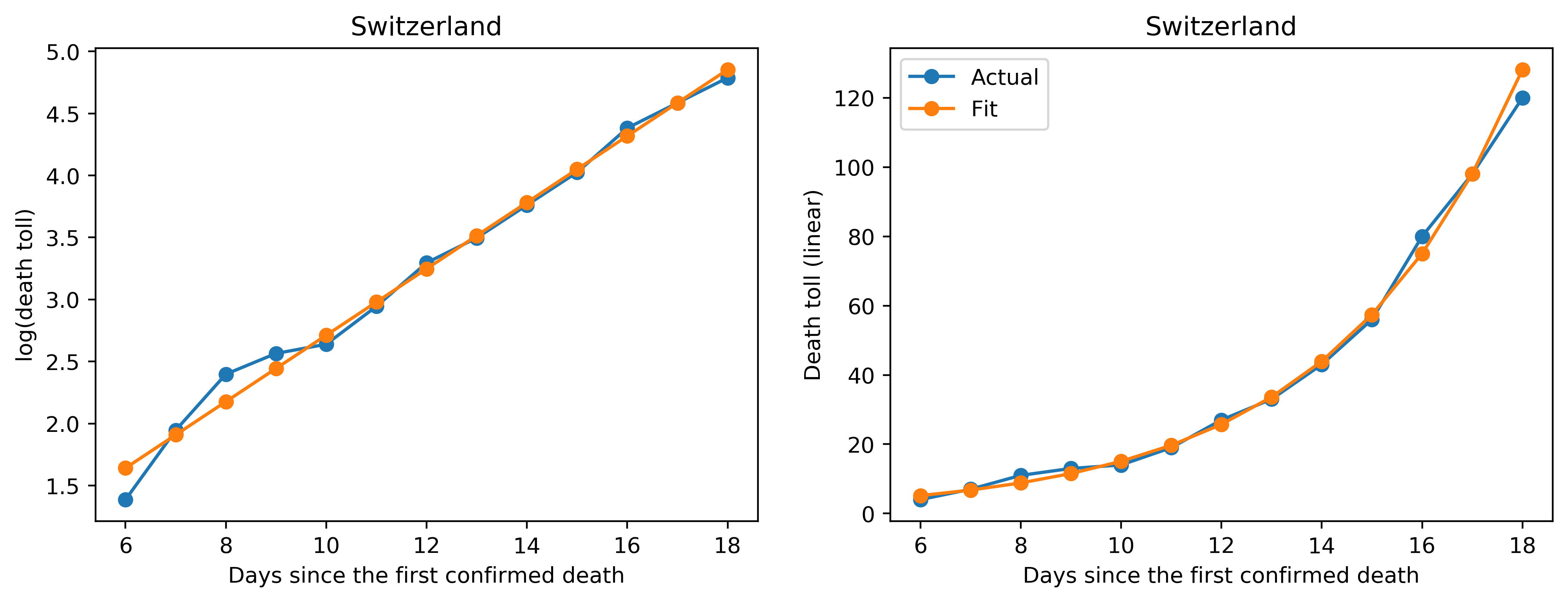
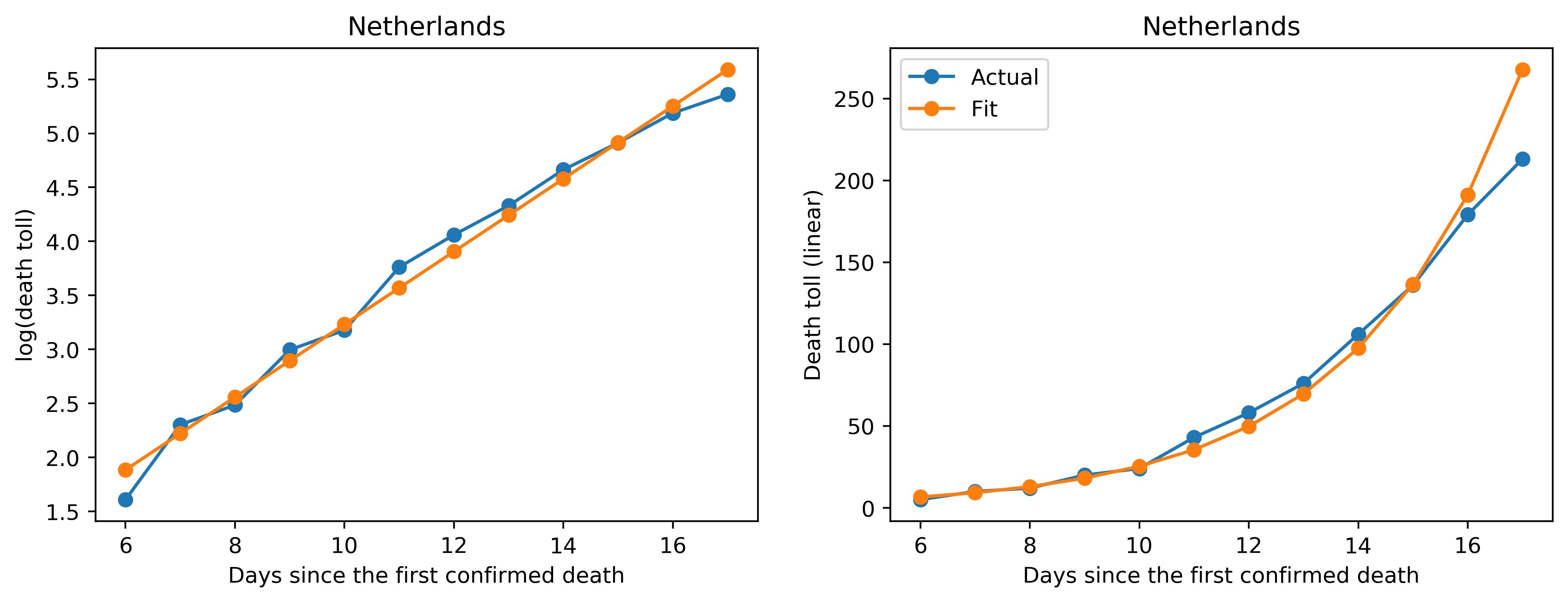
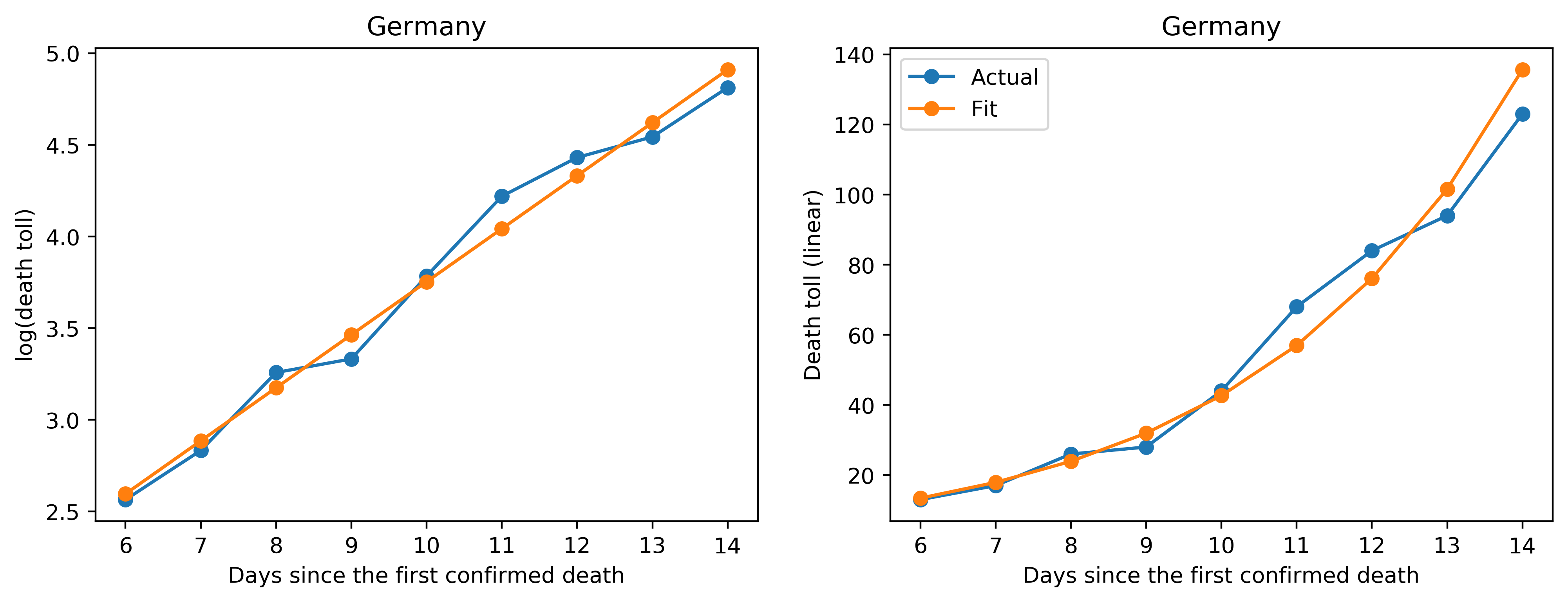
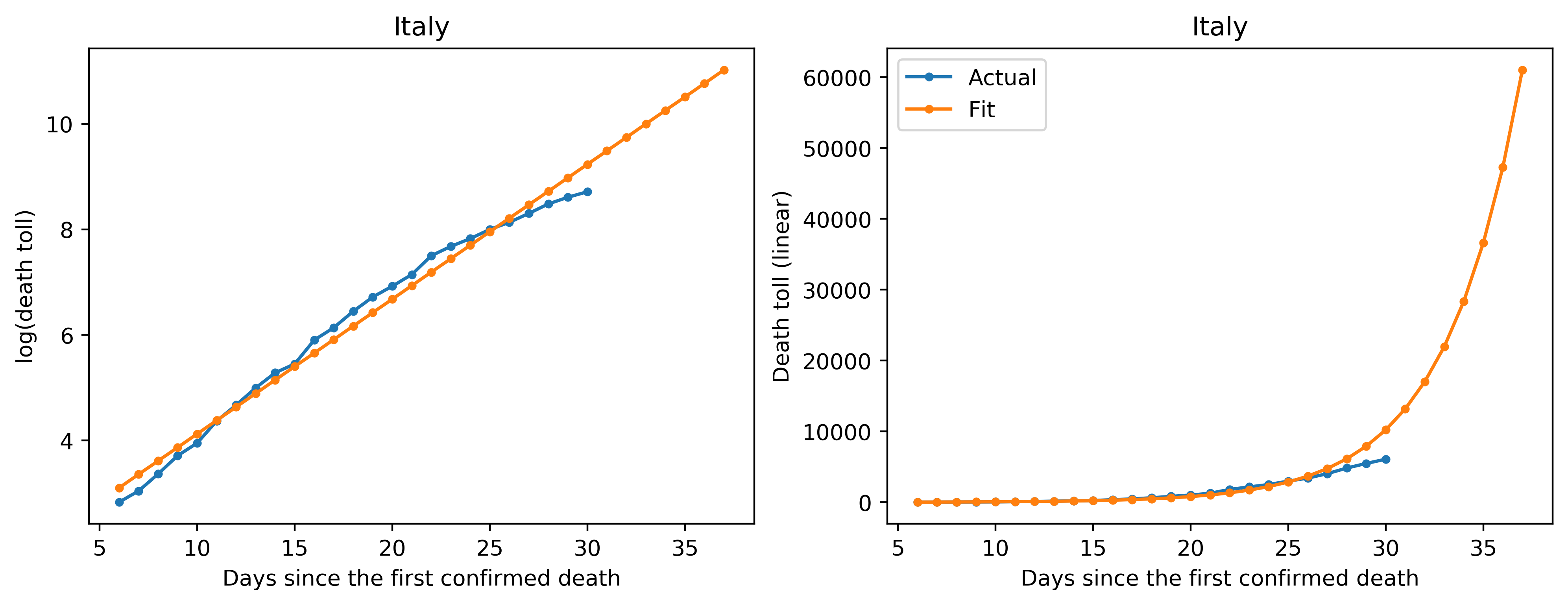
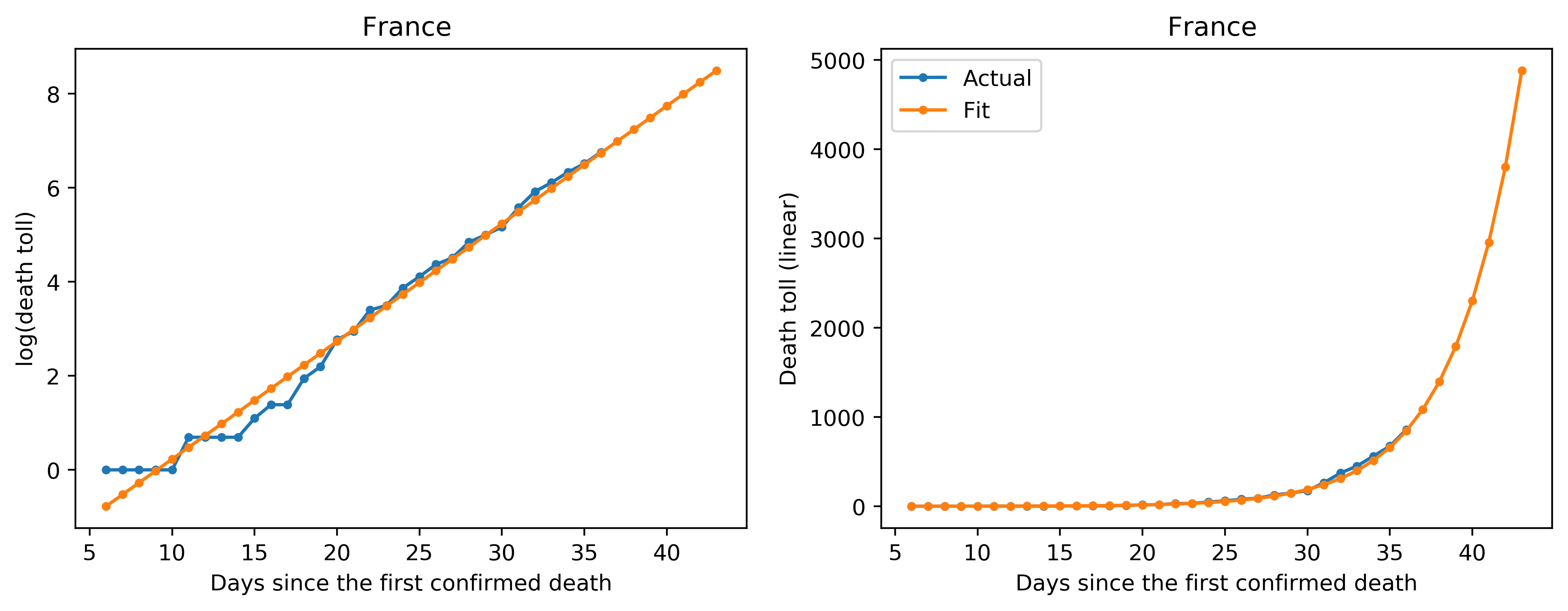
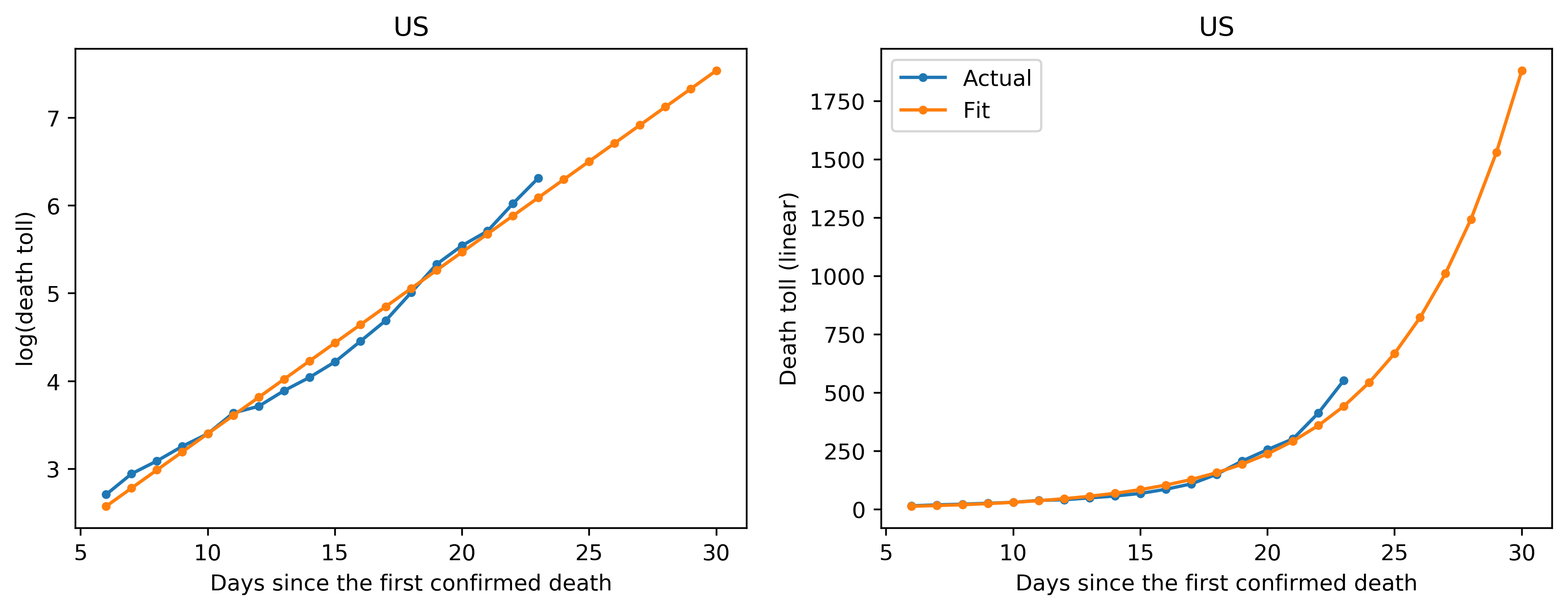
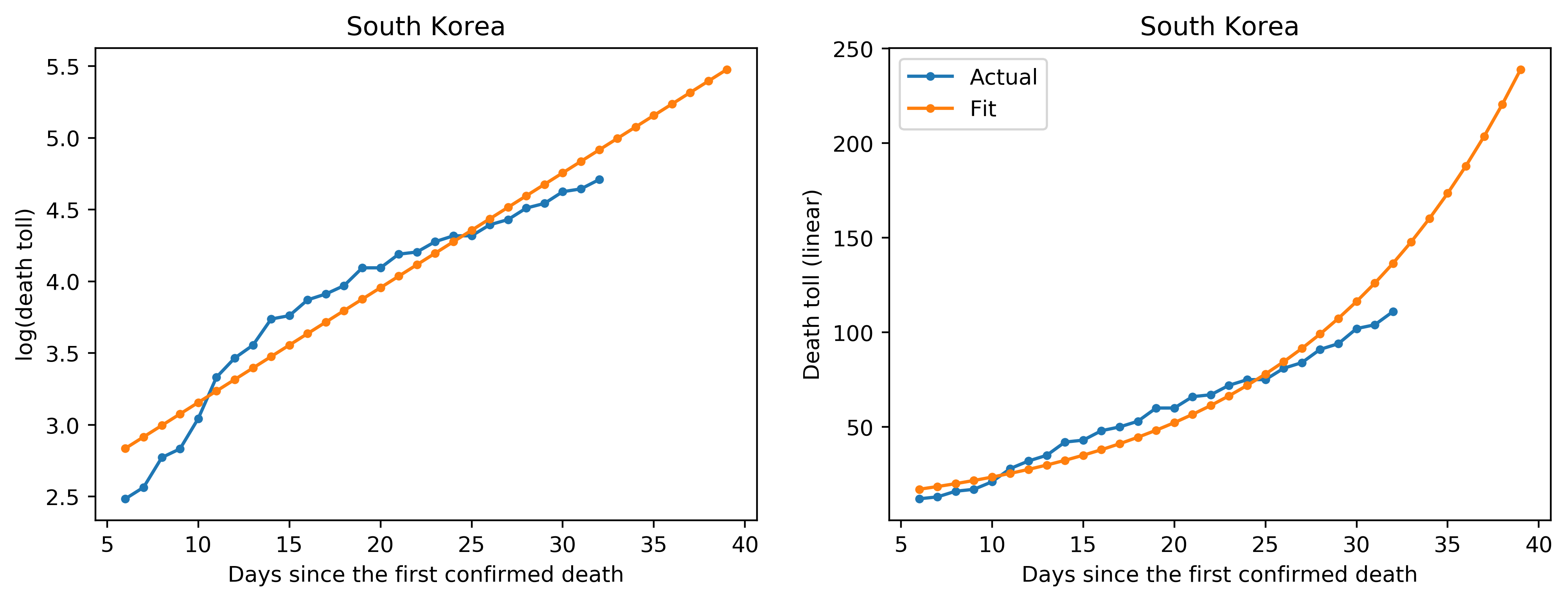
次にプロットを見ていきます。左側のプロットがY軸をlogでプロットしたもの、右側のプロットはY軸がリニアのもので、X軸はどちらも死亡者が最初に確認されてからの日数です。青が実際のデータ、オレンジがフィッティングしたデータになります。
for country in countries:
y = corona_df[country].dropna().values[6:]
ylog = np.log(y)
days = len(y)
x = np.arange(0,days,1,'int')
#plt.plot(x,y)
#plt.plot(x,ylog)
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x,ylog)
doubling = np.log(2)/slope
print(f'{country}: doubling {doubling:.2} days / R^2: {r_value**2:.2}')
fit_y = [np.exp(slope*d+intercept) for d in range(0,days)]
fig,axes=plt.subplots(1,2, figsize=(12,4))
axes[0].plot(x+6,np.log(y),'o-')
axes[0].plot(x+6,np.log(fit_y),'o-')
axes[0].set_title(country)
axes[0].set_xlabel('Days since the first confirmed death')
axes[0].set_ylabel('log(death toll)')
axes[1].plot(x+6,y,'o-')
axes[1].plot(x+6,fit_y,'o-')
axes[1].set_title(country)
axes[1].set_xlabel('Days since the first confirmed death')
axes[1].set_ylabel('Death toll (linear)')
plt.legend(['Actual', 'Fit'])
plt.savefig(f'{country}_fitting.png', dpi=400, bbox_inches='tight')
実際のデータとフィッティングを比較すると、いくつか傾向が見えてきます(あくまで個人的な解釈です)。
(1) データがフィッティングを下回って来ている国
イタリア、イギリスなどでは直近の数日間のデータに関してフィッティングよりも実際のデータが下側に来ています。この1つの解釈としては、ロックダウン(都市封鎖)などにより、感染が抑えられ、その結果死亡者数が減少してきている、という解釈ができるかと思います。例えばイギリスでは先週末あたりからパブ閉鎖などの外出抑制令を出し、かなり厳しい態勢を取ってきましたので(今は外出禁止令になっています)、この効果が出始めているのだと考えられます。また、韓国では実際のデータでは15日目以降から死亡者数が指数関数的ではなく線形で増加しているようにも見えますが(右側のプロット)、MERSのアウトブレイクなどの苦い経験から比較的早い段階から感染に厳しく取り組んできていたので、これもまたその効果が出ているのかと解釈されます(フィッティングという意味ではあまり上手くワークしていないと解釈できますが)。
しかし、上でも述べたようにフィッティングとの乖離が見えてきた段階が初期フェーズの終わりでしたので、これからの状況はウィルス封じ込めが上手く行かなければ中期フェーズに入る可能性があり、まだ全く安心できない状況であると考えられます。
(2) データがフィッティングと一致している国
フランスやスイスなどではデータとフィッティングが綺麗に一致している様子が見られます。これは、まだこれらの国では感染が初期フェーズにある段階だと解釈できます。また、言い換えれば、封じ込めなどの感染対策がまだ効果を発揮していない段階だ、とも解釈できます(これらの国のニュースまでフォローできていないので実際には違うかもしれません)。
(3) データがフィッティングを上回って来ているもの
一方でアメリカではここ数日のデータについては実際のデータがフィッティングよりも上に来ています。これは感染がモデルよりも早く拡大している状況であると解釈できます。しかし、ニューヨークなどの大都市と、ほぼ車ばかりで移動する地方都市とでは感染の広がり方も違うかと言われますので、この解釈が間違っている可能性も十分に考えられますが、かなり注意を要する状況であることは間違いありません。
推定する
次に、**このフィッティングが合っていると仮定した場合今後1週間でどのような状況になるのか?**を推定してみます。上のグラフ同様、左側のプロットがY軸log、右側がY軸リニアのもので、オレンジがフィッティングしたデータです。
# 何日先まで予測するか
period = 7
# prediction
for country in countries:
y = corona_df[country].dropna().values[6:]
ylog = np.log(y)
days = len(y)
x = np.arange(0,days,1,'int')
#plt.plot(x,y)
#plt.plot(x,ylog)
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x,ylog)
doubling = np.log(2)/slope
print(f'{country}: doubling {doubling:.2} days / R^2: {r_value**2:.2}')
fit_y = [np.exp(slope*d+intercept) for d in range(0,days+period)]
fit_x = np.arange(len(fit_y))
#corona_df[f'{country}_fit'] = fit_y + [np.nan]*(len(corona_df)-len(corona_df[country].dropna()))
fig,axes=plt.subplots(1,2, figsize=(12,4))
axes[0].plot(x+6,np.log(y),'.-')
axes[0].plot(fit_x+6,np.log(fit_y),'.-')
axes[0].set_title(country)
axes[0].set_xlabel('Days since the first confirmed death')
axes[0].set_ylabel('log(death toll)')
axes[1].plot(x+6,y,'.-')
axes[1].plot(fit_x+6,fit_y,'.-')
axes[1].set_title(country)
axes[1].set_xlabel('Days since the first confirmed death')
axes[1].set_ylabel('Death toll (linear)')
plt.legend(['Actual', 'Fit'])
plt.savefig(f'{country}_fitting_withprediction.png', dpi=400, bbox_inches='tight')
国によっては数万人になるという予測のものもありますが、あくまでこれは指数関数的に増加していくと仮定した場合ですので、ありえないぐらい最悪のシナリオと考えてよいかと思います。実際にはフィッティングと実際のデータの乖離が見えてきている国もありますし、死亡者数はロジスティック関数的に増加していくと考えられるため、これよりはずっと少ない数になると思われます。とはいえこの半分、3分の1と考えても1万人を超えるケースもありますので、感染者数がこれよりずっと多いことを考えれば、医療体制的に1国として到底許容できる数ではありません。
日本の場合
次に、日本の場合を見てみます。Worldometerには日本のデータは載っていませんでしたので(なぜ?)、以下のサイトで公開してくださっているCSVファイルを使用しました。
- 都道府県別新型コロナウイルス感染者数マップ(ジャッグジャパン株式会社提供)
https://gis.jag-japan.com/covid19jp/
フィッティングについては14日目以降のデータについて行いました。
country = 'Japan'
period = 7
# Data obtained from
# https://gis.jag-japan.com/covid19jp/?fbclid=IwAR30DDBBnQRcXnIOoqJmjbs-Z4kYIS0LvHMBqwBbORWRV3TpjYstvrrBrE4
japan_df = pd.read_csv('COVID-19.csv')
tmp = japan_df[['確定日','死者合計']].dropna()
y = japan_df['死者合計'].dropna().values[14:]# count from Feb 13
ylog = np.log(y)
days = len(y)
x = np.arange(0,days)
# plt.plot(x,y)
# plt.plot(x,ylog,'o-')
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x,ylog)
doubling = np.log(2)/slope
print(f'{country}: doubling {doubling:.2} days / R^2: {r_value**2:.2}')
fit_y = [np.exp(slope*d+intercept) for d in range(0,days+period)]
fit_x = np.arange(len(fit_y))
# corona_df[f'{country}_fit'] = fit_y + [np.nan]*(len(corona_df)-len(corona_df[country].dropna()))
fig,axes=plt.subplots(1,2, figsize=(12,4))
axes[0].plot(x,np.log(y),'.-')
axes[0].plot(fit_x,np.log(fit_y),'.-')
axes[0].set_title(country)
axes[0].set_xlabel('Days since the first confirmed death')
axes[0].set_ylabel('log(death toll)')
axes[1].plot(x,y,'.-')
axes[1].plot(fit_x,fit_y,'.-')
axes[1].set_title(country)
axes[1].set_xlabel('Days since the first confirmed death')
axes[1].set_ylabel('Death toll (linear)')
plt.legend(['Actual', 'Fit'])
plt.savefig('Japan_fitting_withprediction.png', dpi=400)
Japan: doubling 6.0 days / R^2: 0.95
倍加時間は6日と韓国まではいかないものの、他の国よりもずっと長いこと、死亡者数の絶対値が他国と比べ低く抑えられていることから、感染拡大への試みが功を奏していることが伺えます。また、実際のデータとフィッティングとの乖離も少しですが見えていますので、まだ時間はかかるとは思いますがこのまま収束いていくことを願うばかりです。
おわりに
本稿では非常に単純な線形近似というモデルを用い、フィッティングと実際のデータの乖離・最悪のシナリオの予測、などを通して新型コロナウィルスの現状を把握しようと試みました。繰り返しになりますが、あくまで現状を把握するためのツールですので、今後必ずこうなると主張するようなものではありませんし、いたずらに不安を煽ろうとする意図もありません。現状から見える最悪を予測し、それに備えるためには何が必要か考えるためのFood for thoughtを提供しようとするものです。
また、モデル分析は色々な方法が使えます、例えば線形近似ではなくもっとストレートにロジスティック関数で実際のデータを近似する、などのアプローチも試したりできると思います。もし本稿の内容にご興味を持たれた方は是非ご自分で試してみていただけると幸いです。
最後に、新型コロナウィルス対策に日々必死で頑張っておられる各国の医療関係者の方々、感染対策チームの方々に感謝を申し上げて締めくくりたいと思います。