はじめに
いわずもがなJuliaは科学計算に向いたプログラミング言語ですが、微分方程式の数値計算の日本語での解説があまりなかったので、自分で試行錯誤した時のログを元に簡単な解説を書いてみる。
もともとの動機はMatlabで常微分方程式の計算が遅すぎて使い物にならなかったので、別の方法を探していたのがJuliaを使うようになったきっかけ。使用したSundialsライブラリはJulia専用ではなく、いろんな言語で使用できて、Matlabでも使うことができるが、Windows10 64bitで使うにはちょっと手間が必要。ということでMatlabに似た言語であるJuliaを使ってみようという事に。
実際に使用したパッケージはSundials.jlだが、それより使い勝手のいいDifferentialEquations.jlを最近発見したので、こっちを使った場合も載せておく。
セットアップ
Juliaは入ってるものとする。Emacs+ESSでJuliaを実行するのに以下のように設定
;; ESS - Emacs Speaks Statistiscs (for R and Julia)
(add-to-list 'load-path "ESSへのパス")
(load "ess-site")
;; julia
(setq inferior-julia-program-name "juliaバイナリへのパス")
Julia関連パッケージのインストール。DifferentialEquations.jlとParameterizedFunctions.jl、そしてグラフをプロットするのにPlots.jl。CSVファイルを読み込んだりするのであればDataFrames.jlも。
Pkg.update()
Pkg.add("DifferentialEquations") # Sundials.jlはここで一緒にインストールされる
Pkg.add("Plots")
Pkg.add("DataFrames") # optional
# ちゃんと読み込めるか確認(&初回プリコンパイル)
using DifferentialEquations
using Sundials
using Plots
ひたすら待つ。
旧バージョンでのSundials.jlのインストール
最新のバージョンでは問題なくインストールできるはずだが、以前のバージョンでは https://cache.e.ip.saba.us/ のセキュリティ設定?のためSundials.jlがすんなりインストール出来なかった。今後もし同じようなエラーが出たときのために一応対処法をメモしておく。
Pkg.update()
Pkg.add("Sundials")
とすると以下のようなエラーが出る(Windows 10での場合)
LoadError: failed process: Process(`powershell -Command '(new-object net.webclient).DownloadFile("https://cache.e.ip.saba.us/https://bintray.com/artifact/download/tkelman/generic/sundials-2.5.0.7z", "C:\cygwin64\home\user\.julia\v0.4\Sundials\deps\downloads\sundials-2.5.0.7z")'`, ProcessExited(1)) [1]
while loading C:\cygwin64\home\user\.julia\v0.4\Sundials\deps\build.jl, in expression starting on line 37
そこで、sundialsバイナリを https://bintray.com/artifact/download/tkelman/generic/sundials-2.5.0.7z から手動でダウンロードし、Juliaがインストールされているディレクトリ(~/.julia/v0.5/Sundials/deps/downloads など)に保存。そこから
Pkg.build("Sundials")
Pkg.test("Sundials")
ここで "INFO: Sundials tests passed" というメッセージが出ればインストール完了。
Van der Pol方程式のシミュレーション
例としてリミットサイクルを示すVan der Pol振動子をシミュレートしてみる。用いた式はこちら。
\frac{dx}{dt} = y \\
\frac{dy}{dt} = -\mu (x^2 - 1)y - x
特に難しいことは考えず、チュートリアル等を参考に関数を定義し数値計算を行う。(参考:Sundialsでの例、DifferentialEquationsでの例)
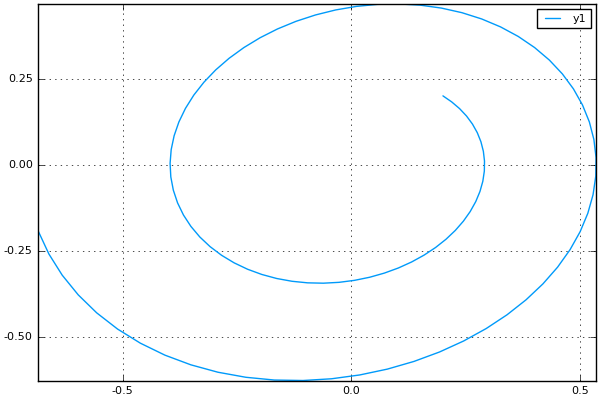
Sundialsを使った場合
using Sundials
using Plots
# 非線形パラメータ
mu = 0.2
# 関数定義
function vdp_sun(t, u, du)
# dx/dt
du[1] = u[2]
# dy/dt
du[2] = mu * (1.0 - u[1]^2.0) * u[2] - u[1]
du
end
# パラメータ設定
u0 = [0.2; 0.2]
t = [0.0:0.1:10.0;]
# メインの計算
res = Sundials.cvode(vdp_sun, u0, t); # u0とtの順序に注意(関数定義と逆)
# プロット
x = [a for a in res[:,1]]
y = [a for a in res[:,2]]
plot(x,y)
savefig("vdp_sundials.png")
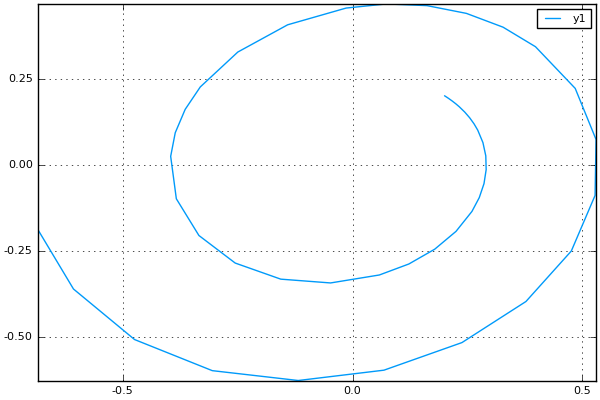
DifferentialEquationsを使った場合
using DifferentialEquations
using Plots
# 非線形パラメータ
mu = 0.2
# 関数定義
function vdp(t, u, du)
# dx/dt
du[1] = u[2]
# dy/dt
du[2] = mu * (1.0 - u[1]^2.0) * u[2] - u[1]
end
# パラメータ設定
u0 = [0.2; 0.2]
tspan = (0.0,10.0)
# メインの計算
prob = ODEProblem(vdp,u0,tspan)
sol = solve(prob, CVODE_BDF(), dt=0.01) # Sundialsのアルゴリズムを使う
# プロット
x = [u[1] for u in sol.u]
y = [u[2] for u in sol.u]
plot(x,y)
savefig("vdp_diffeq.png")
んん?粗い、、、、dtでステップサイズを固定してるはずなのに、adaptiveにステップサイズが決められているようだ。
(要調査 分かる人いたら教えてください)
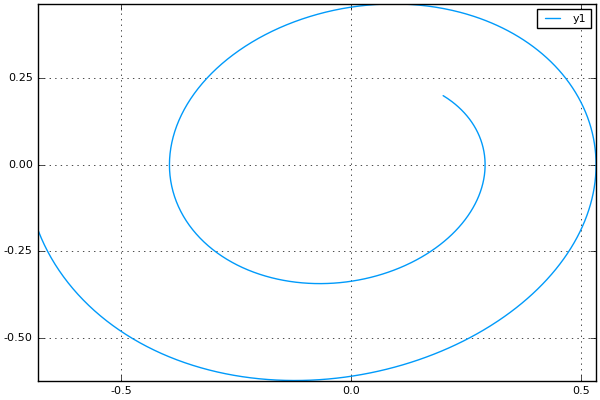
比較のためODE.jlでもやってみる。
using ODE
mu = 0.2
function vdp_ODE(t, u)
# dx/dt
dx_dt = u[2]
# dy/dt
dy_dt = mu * (1.0 - u[1]^2.0) * u[2] - u[1]
# return du
[dx_dt; dy_dt]
end
u0 = [0.2; 0.2]
t = 0:0.01:10.0
(t, pos) = ode45(vdp_ODE, u0, t)
x = [u[1] for u in pos]
y = [u[2] for u in pos]
plot(x,y)
savefig("vdp_ode.png")
こっちは大丈夫。というか明確にステップサイズを指定しているので当たり前だけど。
実行速度比較
Juliaは1回目の実行に時間がかかることがあるので、2回目以降を計測。環境はCore i3-3217U、8GB、Windows 10 64-bit。
sol = solve(prob, CVODE_BDF(), dt=0.01);
for i in 0:3
@time sol = solve(prob, CVODE_BDF(), dt=0.01);
end
res = Sundials.cvode(vdp_sun, u0, t);
for i in 0:3
@time res = Sundials.cvode(vdp_sun, u0, t);
end
(t, pos) = ode45(vdp_ODE, u0, t);
for i in 0:3
@time (t, pos) = ode45(vdp_ODE, u0, t);
end
実行結果は以下
# Sundials.jl
0.000547 seconds (1.25 k allocations: 33.453 KB)
0.000481 seconds (1.25 k allocations: 33.453 KB)
0.000477 seconds (1.25 k allocations: 33.453 KB)
0.000584 seconds (1.25 k allocations: 33.453 KB)
# DifferentialEquations.jl
0.001087 seconds (1.55 k allocations: 45.375 KB)
0.000908 seconds (1.55 k allocations: 45.375 KB)
0.000871 seconds (1.55 k allocations: 45.375 KB)
0.001277 seconds (1.55 k allocations: 45.375 KB)
# ODE.jl
0.001204 seconds (3.37 k allocations: 109.469 KB)
0.001843 seconds (3.37 k allocations: 109.469 KB)
0.001066 seconds (3.37 k allocations: 109.469 KB)
0.001506 seconds (3.37 k allocations: 109.469 KB)
Sundialsが圧倒的にパフォーマンスが良く、ODEが一番悪いという結果に。何回かやってみたが数字は毎回違っているが、全体的に同じ傾向。DifferentialEquantionsではadaptiveにステップサイズを変えたりしているにも関わらずあまり良くない結果というのはすこし驚き。というかそのせいで遅くなっているのかもしれない。
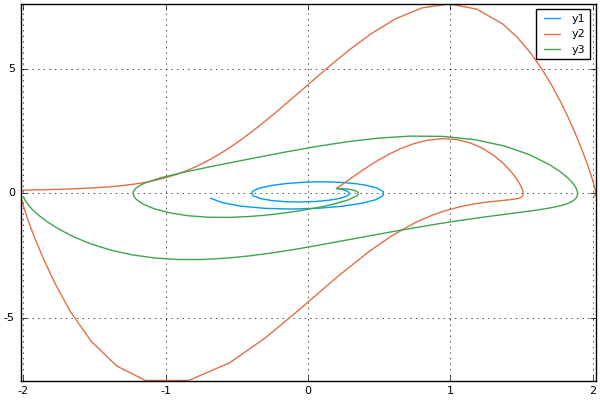
ただDifferentialEquantionsにはいろいろ利点があり、例えばParameterizedFunctions.jlと組み合わせてパラメータの数値を色々変えたインスタンスを生成できたりする。
ちなみに定義の際、=>で定義するとmutableに、=で定義するとimmutableになる。
using ParameterizedFunctions
f = @ode_def VdP begin
du[1] = u[2]
du[2] = mu * (1.0 - u[1]^2.0) * u[2] - u[1]
end mu=>0.2
# デフォルトではmu=0.2
prob = ODEProblem(f,u0,tspan)
sol = solve(prob, CVODE_BDF(), dt=0.01)
x = [u[1] for u in sol.u]
y = [u[2] for u in sol.u]
plot(x,y)
# パラメータmuを変更
f.mu = 5.0
prob = ODEProblem(f,u0,tspan)
sol = solve(prob, CVODE_BDF(), dt=0.01)
x = [u[1] for u in sol.u]
y = [u[2] for u in sol.u]
plot!(x,y)
# mu=1.0のインスタンス g を生成
g = VdP(mu=1.0)
prob = ODEProblem(g,u0,tspan)
sol = solve(prob, CVODE_BDF(), dt=0.01)
x = [u[1] for u in sol.u]
y = [u[2] for u in sol.u]
plot!(x,y)
savefig("vdp_parameterized.png")
まとめ
- Sundials.jlとDifferentialEquations.jlを用いて常微分方程式の数値計算を行った。
- 速度重視であればSundials、機能・利便性重視であればDifferentialEquationsを用いるのが良さげ
- ただし速度の方は1例だけなので逆の結果になる場合もあるかも