こんにちは。@snuffkin と言います。
これは、「数学とコンピュータ Advent Calendar 2017」の17日目の記事です。
20兆円がかかった数学の問題
「数学って何の役に立つの?」
良く聞く言葉だと思います。
これには、いろいろな回答ができると思いますが、数学の問題を解いて懸賞金がもらえると言われたらどうでしょうか?
少し興味が湧きませんか。
数学の世界には、100万ドル(約1億円)の懸賞金がかかった問題がいくつかあります。
それが、
と呼ばれているものです。
この中の問題を解くと、クレイ数学研究所という機関から100万ドルがもらえます。
100万ドルってすごいと思うのですが、実はもっとすごい問題があります。
なんと、20兆円(時価)がかかった問題があるんです。
それが、楕円曲線離散対数問題(Elliptic Curve Discrete Logarithm Problem, 以下 ECDLPと書きます)という問題です。
20兆円って?
本当にそんな問題あるの?
解けたとして、誰が20兆円(時価)も払うの?
そんな疑問がありますよね。
その答えは、流行りの仮想通貨ビットコインです。
ビットコインは、取引している情報を暗号化するのに公開鍵暗号方式と呼ばれる暗号を利用しています。
雰囲気を伝えるページはこちらがオススメで、
数学的にちゃんと知りたい方はこちらがオススメです。
この暗号は、ECDLPを解くことで、解読できることが知られています。
ちなわち、ECDLPを解ければ、ビットコインの取引情報を解読して、流通しているビットコインを自分宛てに送信する、なんてことができます。
なので、ビットコインの時価総額20兆円がかかった問題なのです。
ただ、現実的な時間でECDLPを「一般的に」解くアルゴリズムは、量子コンピュータを利用した方法しか発見されていません。
(実は、NSAあたりがバックドアを知っている可能性もゼロではないかもしれませんが。。。)
もちろん、ECDLPを解けるサイズの量子コンピュータはまだ実現していません。
また、「一般的に」と書いたのは、「特殊な」楕円曲線の場合は現実的な時間で解読できる方法が見つかっているからです。
ビットコインなどで利用している楕円曲線は、こういう「特殊な」楕円曲線を使わないようにしています。
言わずもがなだと思いますが、この問題を本当に解いて、ビットコインにアタックした場合は、何らかの犯罪になる可能性があります。
良い子は本当にアタックしないでください!
楕円曲線離散対数問題
ECDLPがどういったものか、具体的に説明します。
$p$を素数とします(厳密には$p$の選び方にもう少し条件があります)。このとき、有限体$\mathbb{F}_p$上で定義される曲線$E$
y^2 = x^3 + 7
を楕円曲線(Elliptic Curve)と言います(汎用的な定義は、この形でなくても良いのですが、ここではこの形とします)。
このとき、$E$上の点$P=(x_P, y_P), Q=(x_Q, y_Q)$に対し、
\lambda = \begin{cases}
\displaystyle \frac{y_P - y_Q}{x_P - x_Q} & (x_P\neq x_Q) \\
\\
\displaystyle \frac{3x_P^2}{2y_P} & (x_P = x_Q)
\end{cases}
とし、
\begin{align}
x_R &= \lambda^2 -x_P -x_Q \\
y_R &= \lambda(x_P-x_R) -y_P
\end{align}
とおきます。$R=(x_R, y_R)$とすると、点$R$は$E$上にあります($y_R^2 = x_R^3 + 7$を満たします)。
さらに、$P$と$Q$の和を
R := P + Q
と定義することで、楕円曲線$E$にアーベル群の構造が入ることが知られています。
この和を利用して、
2P := P + P, 3P := 2P + P,..., nP := (n-1)P + P
と再帰的に定義することで、$nP$($P$の整数倍の点)を定義することができます。これを$P$の**$n$倍点**と言います。
定義
$G$を楕円曲線$E$上の点とし、$G$で生成される巡回群を$\langle G\rangle$とする。
$P\in\langle G\rangle$に対し、$P=nG$となる$n$を楕円曲線離散対数と呼ぶ。
また、任意に選んだ$P$から$n$を求める問題を、**楕円曲線離散対数問題(ECDLP)**と呼ぶ。
この問題は、素数$p$が小さなときは総当たりで簡単に解けるのですが、巨大な素数になると現実的な時間では解く方法が知られていません。
ビットコインの楕円曲線離散対数問題
実際のビットコインは256ビットの数が使われており、
\begin{align}
p &= 2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 \\
&= 115792089237316195423570985008687907853269984665640564039457584007908834671663
\end{align}
という素数が使われています。
また、巡回群の生成元$G=(x_G, y_G)$として具体的には、
\begin{align}
x_G &= 55066263022277343669578718895168534326250603453777594175500187360389116729240 \\
y_G &= 32670510020758816978083085130507043184471273380659243275938904335757337482424
\end{align}
が使われています。そして、
\langle G\rangleの位数 = 115792089237316195423570985008687907852837564279074904382605163141518161494337
となっています。
ここで、$p$も、巡回群の位数も、$3$で割ると$1$余る素数になっています。
当てずっぽうにECDLPの$n$を見つけようとしても、「$1/$巡回群の位数」の確率でしか楕円曲線離散対数を見つけることができません。
この問題は、どうやって解いたら良いのでしょうか?
まず、ここまで具体的な楕円曲線が決まっているため、この20兆円の問題を解くには、一般のECDLPを解く必要はありません。
この楕円曲線のECDLPだけでも解ければ十分です。
また、数学的に厳密に解く必要もありません。
当てずっぽうだと「$1/$巡回群の位数」の確率でしたが、「$1/256$」の確率で解けたとしても実用上は、クリティカルでしょう。
問題へのアプローチ
問題へのアプローチを具体的に考えてみましょう。簡単のため、$p=61$として、考えてみます。
この場合の楕円曲線は次のようになります。
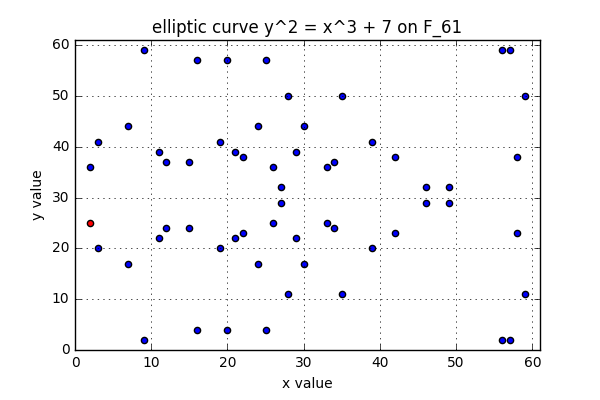
上の図の赤い点$G=(2, 25)$は位数$61$の巡回群の生成元になっています。
$p$と位数が同じなのは偶然で、一般には異なる値になります。
というか、$p$と位数が同じ楕円曲線はanomalous曲線と呼ばれ、**SSSA攻撃法(Semaev-Smart-Satoh-Araki Attack)**という$p$進数体$\mathbb{Q}_p$上の楕円曲線を利用した方法により、鍵長に対して多項式時間でECDLPを解けることが知られています。
そのため、anomalous曲線のように「特殊な」楕円曲線は絶対に実用しないでください!
さて、上の図の見方を変えて、$nG$の$x$座標と$n$の関係を図にすると次のようになります。
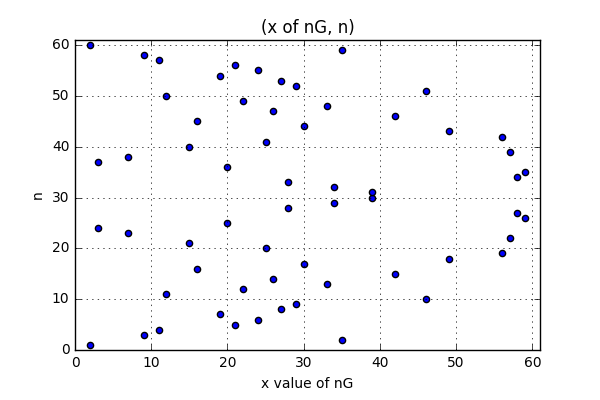
これは上下で対称であるため、$n$の最大値を$p/2$として図にすると次のようになります。
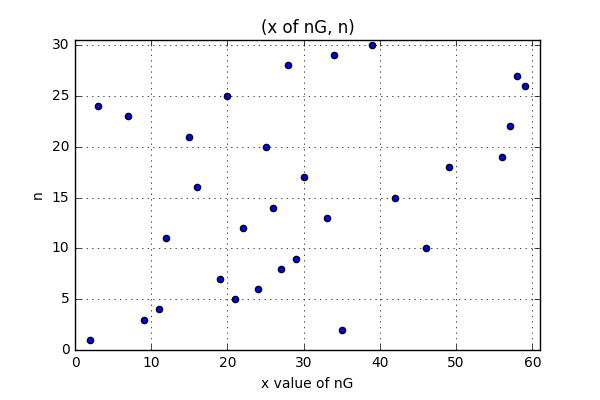
ECDLPは、入力$x$に対して出力$n$する問題です。
言い換えると、この図の点を通るような曲線を求めことができれば、ECDLPを解くことができるのです。
($x$が決まったときに$y^2 = x^3 + 7$を満たす$y$が$2$つ存在しますが、一方の解$(x_0, y_0)$が求まればもう一方の解は$(x_0, -y_0)$になります。そのため、一方が求まれば良い)
そこで、ディープラーニングを使って、この図の点を通る曲線を求めてみましょう。
もちろん、実用的には精度100%である必要はありません。
それなりの精度であれば合格でしょう。
ソフトウェアの準備
私の個人的な好みから、Pythonを使うことにします。
そのため、次のソフトウェアを利用します。
私はWindows環境なので、Windows版のSageMathを利用します。
次のページに従うと、Windows版のSageMathのインストールは簡単です。
次にSageMath上でChainerを使えるようにします。
SageMath Shellを管理者モードで起動して次のコマンドを実行します(pipのupgradeは必須ではありません)。
sage -pip install --upgrade pip
sage -pip install chainer
私の環境では、Chainerのインストール時に次のようなエラーがでました。
Collecting chainer
Using cached chainer-3.2.0.tar.gz
Collecting filelock (from chainer)
Using cached filelock-2.0.13.tar.gz
Complete output from command python setup.py egg_info:
Traceback (most recent call last):
File "<string>", line 1, in <module>
File "/tmp/pip-build-4oSYHq/filelock/setup.py", line 32, in <module>
from filelock import __version__
ImportError: No module named filelock
そのため、filelockをGitHubから取得してインストールし、その後にchainerをインストールするとうまく行きました。
git clone https://github.com/benediktschmitt/py-filelock.git
cd py-filelock
sage -python setup.py install
これで、ソフトウェアの準備の準備ができました。
さて、いよいよChainerを使った具体的な計算なのですが、この記事のボリュームが想像以上で、1回では書ききれませんでした(ごめんなさい)。
ここから先は次回に続きます^^