背景

機械学習の手法のひとつであるクラスタリングは、データの特徴により分類を行います。クラスタリングには様々な手法がありますが、その多くは距離関数を利用して有限個の点を分類します。

昨今、IT業界で機械学習がブームになっていますが、クラスタリング手法の能力について、理論的な視点からあまり言及されていないのではないかと思います(あくまでも、IT業界内の話)。利用している手法で「できること」だけでなく、「できないこと」をハッキリさせるのも重要なことだと思います。実際、Kleinbergさんの論文¹などで、クラスタリングの能力・定式化について研究されています。

Kleinbergさんの論文¹では、クラスタリングの特徴の中からスケール不変性、豊富性、一貫性を取り上げ、3種すべてを満たすクラスタリングは存在しない、という定理が示されています。これをクラスタリングの不可能性定理(Impossibility Theorem for Clustering)と呼びます。

この記事では、クラスタリング能力の限界を示していて興味深い、クラスタリングの不可能性定理を紹介します。数学を使って真正面から紹介します。

考える対象

$S$ を要素数が2以上の有限集合とします。また、$S$ の分割を $\Gamma$ とします。
意味としては、$S$ がクラスタリングしたい有限集合、$\Gamma$ がクラスタリング結果を表します。

まずは、距離関数、クラスタリング関数、クラスタリングの性質に関する定義を紹介し、その後、不可能性定理に言及します。
この記事で利用している図はWilliamsさんのWebサイト¹より引用させて頂きました。

距離関数(distance function)の定義

関数 $d:S \times S \rightarrow \mathbb R$ が任意の $x, y, z \in S$ に対して以下の条件1～4を満たすとき、$d$ を $S$ の距離関数(distance function)と言います。また、$S$ を距離空間(metric space)と言います。

$d(x, y) \ge 0$
$d(x, y) = 0 \Longleftrightarrow x = y$
$d(x, y) = d(y, x)$
$d(x, z) \le d(x, y) + d(y,z)$

ユークリッド距離など数学的な「距離」とは、この定義を満たすものを指します。

いくつか注意点を記載しておきます。

一般の距離関数の定義としては「$S$が有限集合」という条件は不要です。
クラスタリングの不可能性定理の証明では三角不等式(距離関数の定義の条件4)を利用しないため、実際には距離関数より弱い条件でも成立します。
クラスタリングの不可能性定理では、距離関数を利用したクラスタリング手法について言及しています。そのため、距離関数を利用しないクラスタリング手法にはこの定理は当てはまりません。

距離関数 $d$ と実数 $\beta > 0$ の積 $\beta d$ を

\beta d(x, y) := \beta \cdot d(x, y) \tag{右辺は実数同士の積}

で定めます。すると、$\beta d$ もまた距離関数になります。

クラスタリング関数(clustering function)の定義

有限集合 $S$ と距離関数 $d$ に対して $S$ の分割 $\Gamma$ を対応させる関数 $f$ をクラスタリング関数(clustering function)と呼びます。

f(S, d) = \Gamma

また、$\Gamma$ に属する $S$ の部分集合をクラスタ(cluster)と呼びます。
クラスタリング関数は、有限集合と距離空間を入力とし、分割(=クラスタの集合)を出力する関数です。
これ以降、有限集合 $S$ を固定して考え、$f(S, d)$ のことを単に $f(d)$ と書くことにします。

次に、クラスタリング関数の性質であるスケール不変性、豊富性、一貫性について説明します(この辺の訳語は私が勝手に付けたのですが、しっくりこない場合はすみません)。
これら性質は、感覚的にはクラスタリング関数が満たして欲しい性質です。

スケール不変性(Scale-Invariance)

クラスタリング関数 $f$ が任意の距離関数 $d$ と実数 $\beta > 0$ に対して次の式を満たすとき、スケール不変性(Scale-Invariance)があると言います。

f(\beta d) = f(d)

スケール不変性とは、「$\beta$ 倍に距離が引き延ばされても、クラスタリング結果は変わらない」ということです。

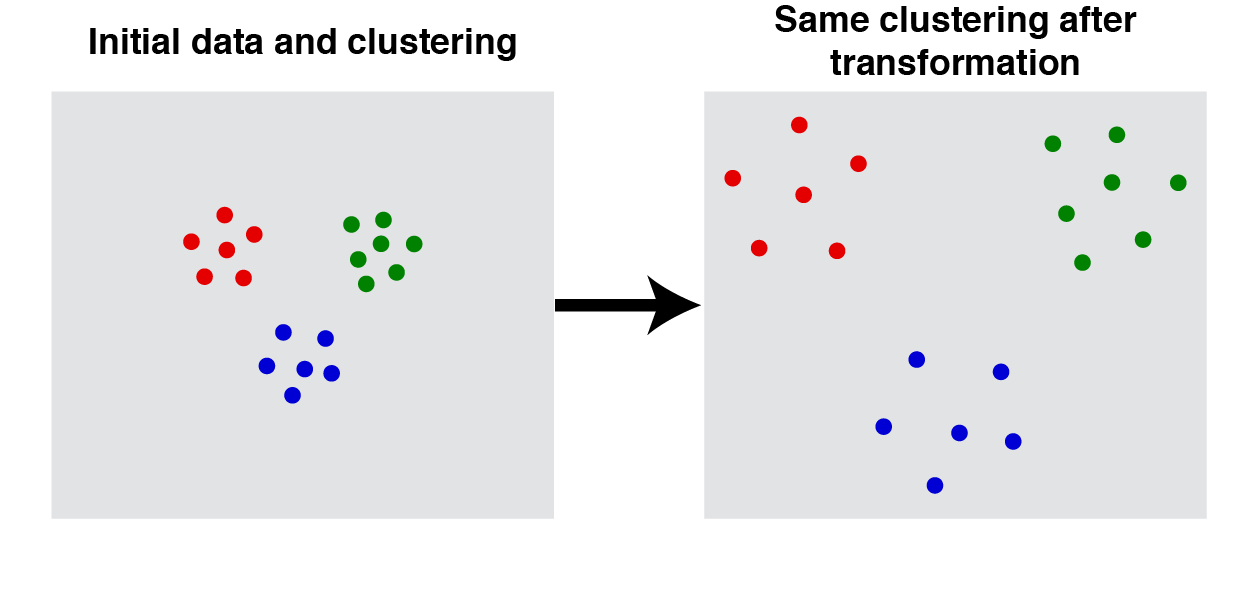
この図では、$S$ の要素の位置が変わっているようにも見えますが、位置が変わらずに距離が伸びているイメージです。

豊富性(Richness)

クラスタリング関数 $f$ の値域(range)を次のように定義します。

Range(f) := \{ S の分割 \Gamma | ある距離関数 d が存在し、f(d) = \Gamma \}

$f$ が以下を満たすとき、豊富性(Richness)があると言います。

Range(f) = \{S の分割\} \tag{1}

(1)の右辺は、距離関数やクラスタリング関数に関係なく、$S$ に対して可能な(集合論的な)分割全体を表します。

豊富性とは、「距離関数を適切に取れば任意の分割を作ることができる」ということです。この性質は、クラスタリング関数 $f$ が全射であることを意味するため、文献によっては豊富性のことを全射性(Surjectivity)と呼んでいます(個人的には「Richness」より「Surjectivity」の方がしっくりきます)。

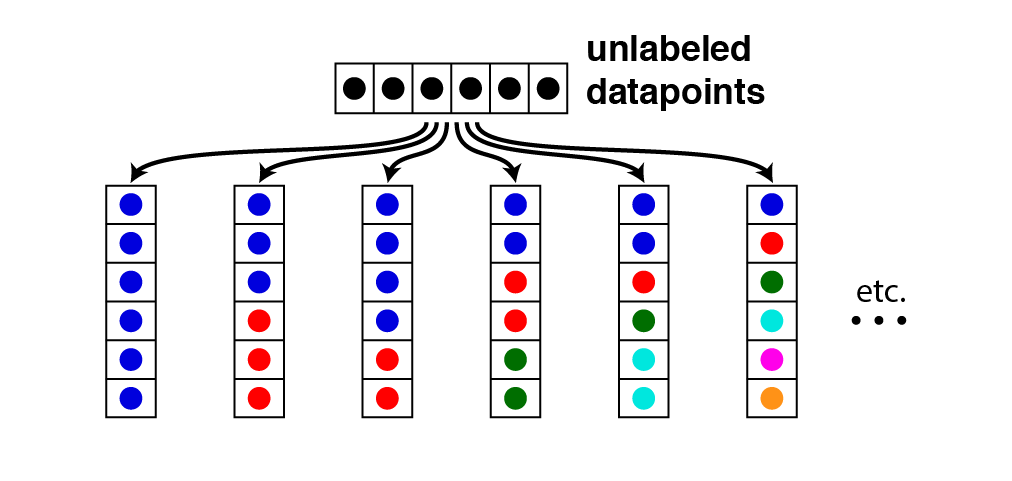
この図では、"unlabeled datapoints"と書かれた $S$ の要素が様々なクラスタに分割される様子を表しています(同じ色が同じクラスタを表しています)。

一貫性(Consistency)

$\Gamma$ を $S$ の分割とし、$d, d'$ を $S$ の距離関数とします。
すべての $x, y \in S$ に対し次の条件1～2を満たすとき、$d'$ を $d$ の$\Gamma$ 変換($\Gamma$- transformation)と言います。

$x, y$ が $\Gamma$ の同じクラスタに属する $\Longleftrightarrow d'(x, y) \le d(x, y)$
$x, y$ が $\Gamma$ の別のクラスタに属する $\Longleftrightarrow d'(x, y) \ge d(x, y)$

$\Gamma$ 変換は、同じクラスタのものをより近くに、別クラスタのものをより遠くに写します。

$\Gamma=f(d)$とし、$d$ の任意の $\Gamma$ 変換 $d'$ に対して、

f(d) = f(d')

となるとき、$f$ は一貫性(Consistency)があると言います(「整合性」とか「無矛盾性」と訳した方がしっくりくる人もいるかもしれせまん)。
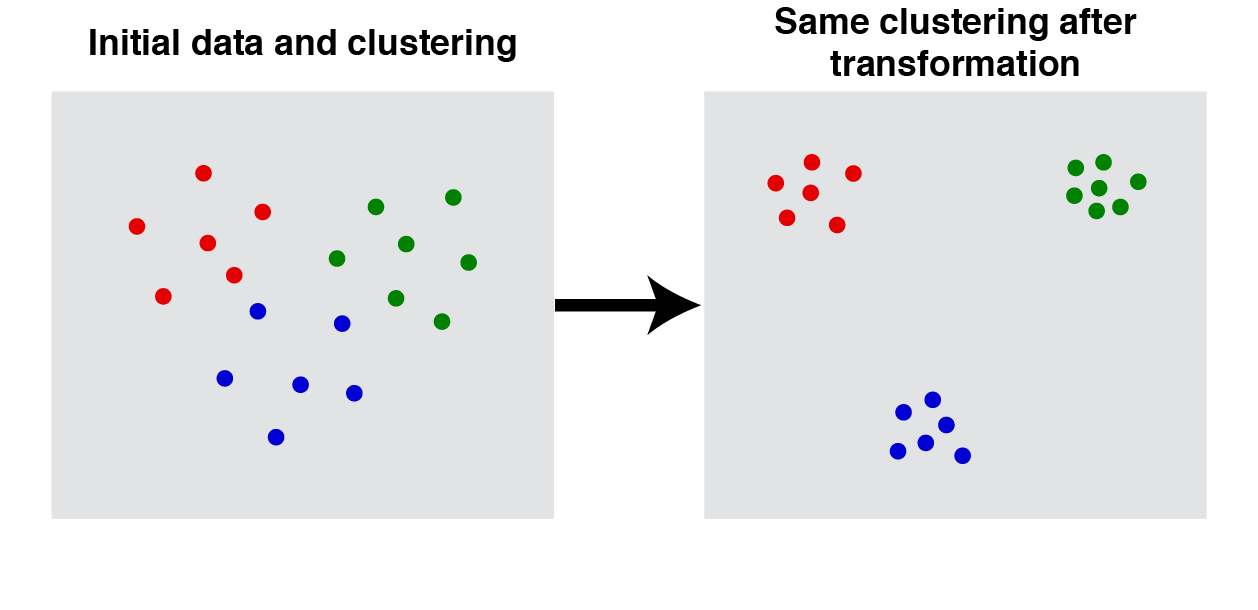
一貫性とは、「同じクラスタのものをより近くに、別クラスタのものをより遠くに写しても、クラスタリング結果は変わらない」ということです。

ここまで、クラスタリング関数のスケール不変性、豊富性、一貫性について説明してきました。もう一度言いますが、これらの性質は、感覚的にはクラスタリング関数が満たして欲しい性質です。

これで、クラスタリングの不可能性定理について説明する準備ができました。具体的な定理の内容について説明します。

クラスタリングの不可能性定理(Impossibility Theorem for Clustering)

$S$ の要素数が2以上であるとき、以下の条件1～3すべてを満たすクラスタリング関数は存在しない。

スケール不変性

豊富性

一貫性

これをクラスタリングの不可能性定理(Impossibility Theorem for Clustering)と呼びます。
「満たして欲しい性質が3つあるけれど、全部を満たすことはできない」形式の定理のせいか、CAP定理に似た雰囲気を感じます。

この定理は、具体的なクラスタリング手法(アルゴリズム)を規定していないため、適用可能な範囲が広そうに見えます。「距離関数に依存して有限集合を分割する何かしらの手法」全般に適用できそうですね。

不可能性定理の証明

Ackermanさんの論文²、Williamsさんの解説³にしたがって、証明します。
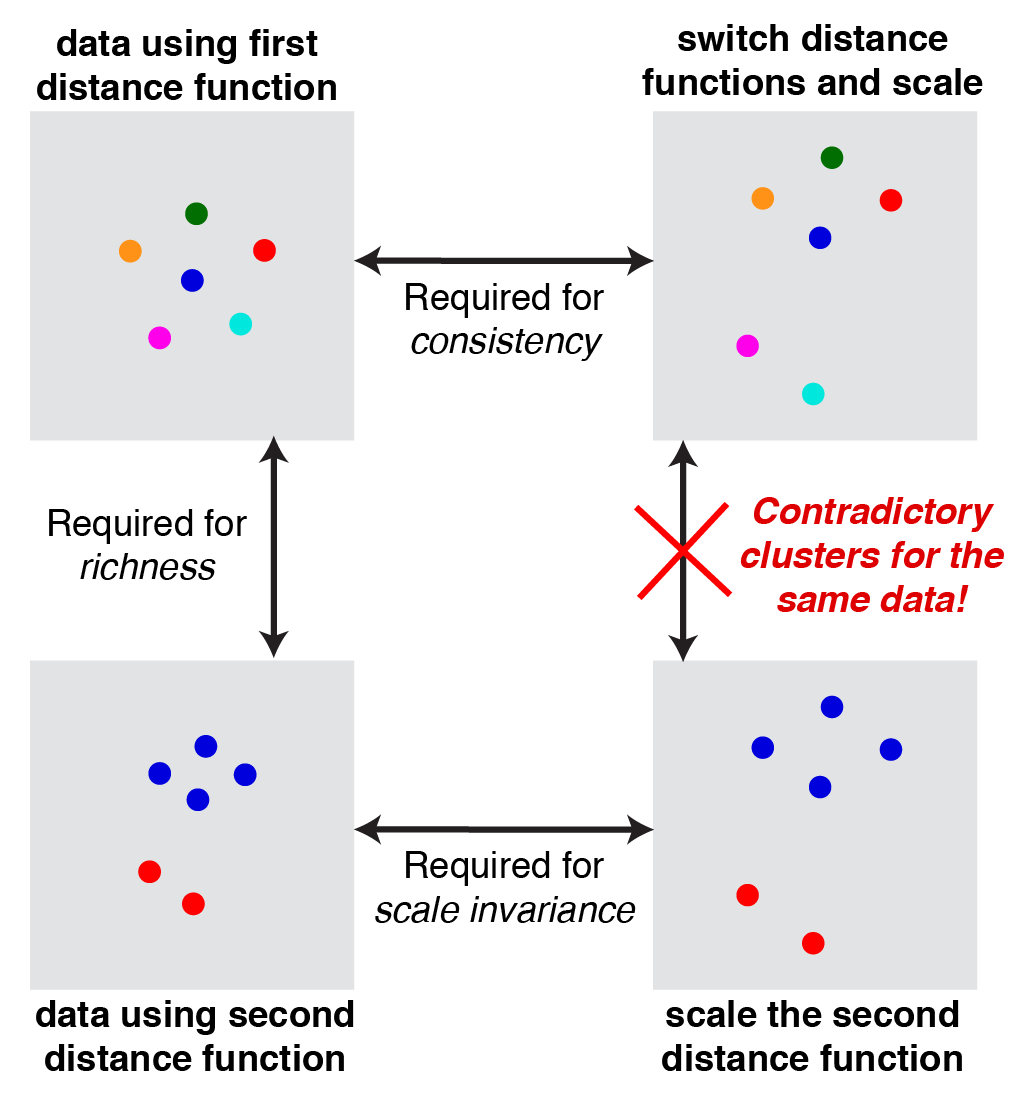
次の図はWilliamsさんの解説³にある図で、証明のイメージを表しています。

$S$ を要素数が2以上の有限集合とし、$f$ をスケール不変性、豊富性、一貫性を満たすクラスタリング関数とします。このとき、矛盾が生じることを示します(背理法)。

$f$ の豊富性より、$f(d_1) \ne f(d_2)$ となるような距離関数 $d_1, d_2$ が存在します。例えば、次のように $d_1, d_2$ を取ります。

$d_1 = S$のすべての要素を別のクラスタにする距離関数(図・左上の"first distance function")
$d_2 = d_1$と異なるクラスタを作る距離関数(図・左下の"second distance function")

$S$ の要素数が2以上なので、例えば「すべての要素を同一クラスタにする距離関数」を $d_2$ として取ることもできます。

ここで、すべての $x \ne y$ に対して

cd_2(x, y) \ge \max \{ d_1(x, y) | x, y \in S \}

を満たすように $c$ を取り、距離関数 $\hat{d}$ を

\hat{d}(x, y) := c \cdot d_2(x, y)

で定まるものとします。すると、すべての $x \ne y$ に対して、

\hat{d}(x, y) = c \cdot d_2(x, y) \ge \max \{ d_1(x, y) | x, y \in S \} \ge d_1(x, y)

となります。$x = y$ の場合は、距離関数の定義の条件2より $\hat{d}(x, y) = 0, d_1(x, y) = 0$ となります。そのため、すべての $x, y \in S$ に対して、

\hat{d}(x, y) \ge d_1(x, y)

が成り立ちます。$d_1$ の定め方を思い返してみると、異なる要素は別のクラスタに写ります。このことから、$\hat{d}$ は $d_1$ の $\Gamma$ 変換になります。そのため、一貫性より $f(\hat{d}) = f(d_1)$ となります。(図・上段にある左右の分割が一致する)

また、スケール不変性より $f(\hat{d}) = f(cd_2) = f(d_2)$ となります。(図・下段にある左右の分割が一致する)

これにより、$f(d_1) = f(\hat{d}) = f(d_2)$ となるため、$f(d_1) \ne f(d_2)$ に矛盾します。

何が困るんでしょうか？

ここでは、クラスタリングの性質が破れていると何が困るのか、考えてみたいと思います。ちょっと大袈裟に書きます。
(この節は論文紹介というより、私の意見です)

スケール不変性が破れていると、距離関数を $\beta$ 倍するとクラスタリング結果が変わることがあります。ということは、良いクラスタリングを得るには、いい感じの $\beta$ を見つけることが必要になります。
例えば、ユークリッド距離をそのまま使う($\beta = 1$)より、0.5倍した方が良いクラスタリングが得られるかもしれないし、2倍した方が良いクラスタリングが得られるかもしれません。いったい $\beta$ は何にすれば良いのでしょうか！

豊富性が破れていると、どのような距離関数を利用しても作りだすことができない分割が存在します。ということは、そもそも自分たちが満足する分割が作れないかもしれません！

一貫性が破れていると、「同じクラスタにしたいものは近く、別のクラスタにしたものは遠くする」と想定して距離関数を考えても、うまくいかないかもしれません。「同じクラスタのものをより近くにしたら、別クラスタになってしまった」「別クラスタのものをより遠くにしたら、同じクラスタになってしまった」ということが起きるかもしれません。こういう感覚的なチューニングが通用しない状況で、どうやっていい感じの距離関数を見つければ良いのでしょうか！

最後に

この記事ではクラスタリング能力の限界を示した「クラスタリングの不可能性定理」について紹介しましたが、どうだったでしょうか。ちょっと違う視点からクラスタリングについて考え、興味をもってもらえたなら幸いです。

結局のところ、(距離関数に依存した)万能なクラスタリングは存在せず、3つの性質のバランスを取る必要があります。例えば、k-means法はクラスタ数kを固定してしまっているため、豊富性を満たしません。(豊富性は、ちょっと厳しい条件に見えます)
3つは無理でも2つの性質を満たすために、Kleinbergさんの論文¹では単連結法による階層的クラスタリング(single-linkage clustering)とその停止条件(stopping condition)という考え方に言及しています。

また、この3つ以外にもクラスタリングの性質は考えられています。
Hopcroftさん、Kannanさんは、豊富性を緩めて3つの性質を満たすクラスタリング関数の存在を示しています⁴。
Williamsさんの論文³を見ると「クラスタリング関数の分類」など様々なことが書いてあるため、勉強になりそうです。
この記事を読んで興味をもった方は、この先の話題をぜひ調べてみてください(そして、教えてください^^)。

参考文献

J. Kleinberg, An impossibility theorem for clustering. In Suzanna Becker, Sebastian Thrun, and Klaus Obermayer, editors, NIPS, pages 446–453. MIT Press (2002). ↩
M. Ackerman, Towards Theoretical Foundations of Clustering. A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Doctor of Philosophy in Computer Science (2012) ↩
A. Williams, Is clustering mathematically impossible?. Web site (2015). ↩
J. Hopcroft, R. Kannan, Foundations of Data Science.(2014) ↩