この文章は「プログラマのための量子アルゴリズム入門」の一部です。
全体の目次・記載方針を確認する場合は、次の画像をクリックしてください。
\newcommand{\TwoOne}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array} \right)}
\newcommand{\TwoTwo}[4]{\left(\begin{array}{cc} #1 & #2 \\ #3 & #4 \end{array} \right)}
\newcommand{\Ket}[1]{\mid #1 \rangle}
\newcommand{\FracTwo}{\frac{1}{\sqrt{2}}}
\newcommand{\Superposition}{\frac{1}{\sqrt{2}}\left(\Ket{0}+\Ket{1}\right)}
\newcommand{\SuperpositionZ}{\frac{1}{\sqrt{2}}\left(\Ket{0}-\Ket{1}\right)}
今回の内容
量子回路について導入を行い、1量子ビットの量子回路について説明します。
ユニタリ行列の具体的な計算を通して、量子ゲートがどのように動作するか確認しながら進めます。
イントロダクション
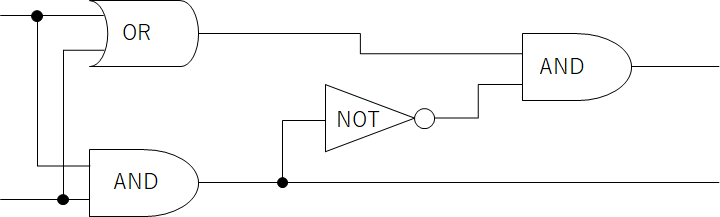
古典ビットを操作するについて説明するとき、論理回路がよく使われます。
例えば、次のような回路図です。
このようにOR, AND, NOT等のゲート(素子)を組み合わせたものが、回路です。この回路に古典ビットを入力することで計算が行われます。これが古典回路です。
量子コンピュータでも、量子ビットを操作する量子ゲート(量子素子、quantum gate)を組み合わせて量子回路(quantum circuit)を作成します。この量子回路に量子状態を入力することで、計算が行われます。
このシリーズで説明するのは「量子ゲート方式」の量子コンピュータですが、この名称は量子ゲートに由来しています。
別方式の量子コンピュータに「量子アニーリング方式」というものがありますが、そちらは量子ゲートを使わずに計算を行います。
第1回で説明したように、ユニタリ発展を行う回路を実装することで量子ビットの状態を変化させ、計算することができます。
量子ゲートを数学的に表現したものがユニタリ行列となります。そのため、量子ゲートとユニタリ行列を同一視して話を進めます。
代表的な1量子ビットの量子ゲート
さて、今回はいくつかの代表的な量子ゲートについて説明します。
それぞれの量子ゲートがどのように動作するか分かるように、具体的な計算例を書きます。
このあたりの手触りを感じたい方は、実際に計算例を追ってみてください。
特に証明しませんが、ここで紹介するものはすべてユニタリ行列( $U^*U=\mathbb{I}$ となる行列)です。
単位行列
単位行列はもっとも基本的な量子ゲートです。
\begin{align}
\mathbb{I} := \TwoTwo{1}{0}{0}{1}
\end{align}
$\mathbb{I}$ により、量子状態 $\Ket{0}, \Ket{1}, \Superposition$ は次のように変化します。
\begin{align}
\mathbb{I}\Ket{0} &= \TwoTwo{1}{0}{0}{1}\TwoOne{1}{0} = \TwoOne{1}{0} = \Ket{0} \\
\mathbb{I}\Ket{1} &= \TwoTwo{1}{0}{0}{1}\TwoOne{0}{1} = \TwoOne{0}{1} = \Ket{1} \\
\mathbb{I}\Superposition &= \TwoTwo{1}{0}{0}{1}\TwoOne{\FracTwo}{\FracTwo} = \TwoOne{\FracTwo}{\FracTwo} = \Superposition
\end{align}
単位行列ですので、元のままですね。
元のままなので使い道がなさそうな気がするとは思いますが、複数の量子ビットを扱うときに「特定の量子ビットを変化させないゲート」として活躍します。
量子回路を書くときには、次のように表記します。
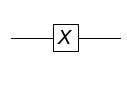
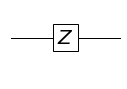
パウリX行列
次は物理学者のパウリさんに由来するパウリ(Pauli)行列です。
パウリ行列にはいくつか種類がありますが、今後よく利用することになる $X$ と $Z$ を紹介します。
$X$ や $Z$ が変数に見えて紛らわしく感じる方もいるかと思います。このシリーズでは、大文字の $X$ や $Z$ は変数としては使わず、パウリ行列を表すことに注意してください。
さて、まずは、パウリ行列 $X$ です。
\begin{align}
X := \TwoTwo{0}{1}{1}{0}
\end{align}
$X$ により、量子状態 $\Ket{0}, \Ket{1}, \Superposition$ は次のように変化します。
\begin{align}
X\Ket{0} &= \TwoTwo{0}{1}{1}{0}\TwoOne{1}{0} = \TwoOne{0}{1} = \Ket{1} \\
X\Ket{1} &= \TwoTwo{0}{1}{1}{0}\TwoOne{0}{1} = \TwoOne{1}{0} = \Ket{0} \\
X\Superposition &= \TwoTwo{0}{1}{1}{0}\TwoOne{\FracTwo}{\FracTwo} = \TwoOne{\FracTwo}{\FracTwo} = \Superposition
\end{align}
パウリ行列 $X$ を使うと $\Ket{0}$ が $\Ket{1}$ に、$\Ket{1}$ が $\Ket{0}$ に変化します。
これにより、ビット反転(bit flip)を実現することができます。古典ゲートでいうとNOTですね。
$\Superposition$ のように同じ確率で $\Ket{0}$ が $\Ket{1}$ 重ね合わせ状態になっている場合、ビット反転しても元の量子状態から変化はありません。
量子回路を書くときには、次のように表記します。
パウリZ行列
次はパウリ行列 $Z$ です。
\begin{align}
Z := \TwoTwo{1}{0}{0}{-1}
\end{align}
パウリ行列 $Z$ により、量子状態 $\Ket{0}, \Ket{1}, \Superposition$ は次のように変化します。
\begin{align}
Z\Ket{0} &= \TwoTwo{1}{0}{0}{-1}\TwoOne{1}{0} = \TwoOne{1}{0} = \Ket{0} \\
Z\Ket{1} &= \TwoTwo{1}{0}{0}{-1}\TwoOne{0}{1} = \TwoOne{0}{-1} = -\Ket{1} \\
Z\Superposition &= \TwoTwo{1}{0}{0}{-1}\TwoOne{\FracTwo}{\FracTwo} = \TwoOne{\FracTwo}{-\FracTwo} = \SuperpositionZ
\end{align}
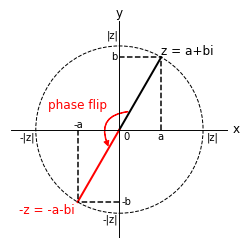
パウリ行列$Z$ は $\Ket{0}$ を変化させませんが、 $\Ket{1}$ の係数の符号を反転させます。
これを、位相反転(phase flip)と言います。
ところで、「位相」とは何のことでしょうか。
複素数 $z=a+bi$ ($a,b$ は実数、$i$ は虚数単位)を次の図のように複素平面にプロットしたとき、$\theta$ を $z$ の位相(phase)と呼びます。
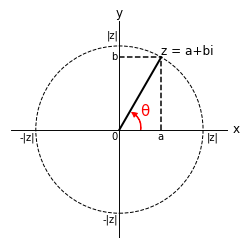
$\Ket{1}$ の係数の符号を反転(-1倍)すると位相が半周変化するため、位相反転と呼ばれます。
量子回路を書くときには、次のように表記します。
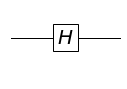
アダマール行列
次は数学者のアダマールさんに由来するアダマール(Hadamard)行列 $H$ です。
\begin{align}
H := \frac{1}{\sqrt{2}}\TwoTwo{1}{1}{1}{-1}
\end{align}
$H$ により、量子状態 $\Ket{0}, \Ket{1}, \Superposition, \SuperpositionZ$ は次のように変化します。
\begin{align}
H\Ket{0} &= \FracTwo\TwoTwo{1}{1}{1}{-1}\TwoOne{1}{0} = \FracTwo\TwoOne{1}{0} = \Superposition \\
H\Ket{1} &= \FracTwo\TwoTwo{1}{1}{1}{-1}\TwoOne{0}{1} = \FracTwo\TwoOne{0}{-1} = \SuperpositionZ \\
H\Superposition &= \FracTwo\TwoTwo{1}{1}{1}{-1}\TwoOne{\FracTwo}{\FracTwo} = \TwoOne{1}{0} = \Ket{0} \\
H\SuperpositionZ &= \FracTwo\TwoTwo{1}{1}{1}{-1}\TwoOne{\FracTwo}{-\FracTwo} = \TwoOne{0}{1} = \Ket{1}
\end{align}
アダマール行列 $H$ を使うと、 $\Ket{0}$ や $\Ket{1}$ から重ね合わせ状態を作ることができます。
逆に $\Superposition, \SuperpositionZ$ という重ね合わせ状態から、$\Ket{0}$ や $\Ket{1}$ を作ることができます。
重ね合わせ状態を作り出して計算する量子アルゴリズムは非常に多いため、今後大活躍する量子ゲートのひとつです。
また、アダマール行列はパウリ行列を使って次のように表すこともできます。
\begin{align}
H = \FracTwo\left(X+Z\right)
\end{align}
量子回路を書くときには、次のように表記します。
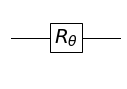
位相シフト行列
次は位相シフト(phase shift)行列です。これは変数 $\theta$ を使って次のように表される行列です。
\begin{align}
R_\theta := \TwoTwo{1}{0}{0}{e^{i\theta}}
\end{align}
$R_\theta$ により、量子状態 $\Ket{0}, \Ket{1}, \Superposition$ は次のように変化します。
\begin{align}
R_\theta\Ket{0} &= \TwoTwo{1}{0}{0}{e^{i\theta}}\TwoOne{1}{0} = \TwoOne{1}{0} = \Ket{0} \\
R_\theta\Ket{1} &= \TwoTwo{1}{0}{0}{e^{i\theta}}\TwoOne{0}{1} = \TwoOne{0}{e^{i\theta}} = e^{i\theta}\Ket{1} \\
R_\theta\Superposition &= \TwoTwo{1}{0}{0}{e^{i\theta}}\TwoOne{\FracTwo}{\FracTwo} = \FracTwo\TwoOne{1}{e^{i\theta}} = \FracTwo(\Ket{0}+e^{i\theta}\Ket{1})
\end{align}
$R_\theta$ は、$\Ket{0}$ を変えませんが $\Ket{1}$ の係数を $e^{i\theta}$ 倍します。
数学的に言えば「 $e^{i\theta}$ 倍する」ことは、「複素平面上で原点を中心に反時計回りに $\theta$ ラジアン回転する」ことと同じです。そのため、位相シフトと呼ばれています。
特に、$\theta=\pi$ のとき、
\begin{align}
R_\pi = \TwoTwo{1}{0}{0}{e^{i\pi}} = \TwoTwo{1}{0}{0}{-1} = Z
\end{align}
となるため、位相シフト行列はパウリ行列 $Z$ (位相反転)を一般化したものと考えることができます。
量子回路を書くときには、次のように表記します。
可逆性について
ここで紹介した行列はどれもユニタリ行列ですが、それらのうち $\mathbb{I}, X, Z, H$ は随伴行列が自分自身に一致します。
\begin{align}
\mathbb{I}^*=\mathbb{I}, \quad X^*=X, \quad Z^*=Z, \quad H^*=H
\end{align}
そのため、自分自身が逆行列になります。
\begin{array}{c}
\mathbb{I}\mathbb{I}=\mathbb{I}^*\mathbb{I}=\mathbb{I}, \quad XX=X^*X=\mathbb{I}, \quad ZZ=Z^*Z=\mathbb{I}, \quad HH=H^*H=\mathbb{I} より \\
\mathbb{I}^{-1}=\mathbb{I}, \quad X^{-1}=X, \quad Z^{-1}=Z, \quad H^{-1}=H
\end{array}
したがって、任意の量子状態 $\Ket{x}$ に対して、次が成り立ちます。
\begin{align}
\mathbb{I}^2\Ket{x} = \Ket{x} \\
X^2\Ket{x} = \Ket{x} \\
Z^2\Ket{x} = \Ket{x} \\
H^2\Ket{x} = \Ket{x} \\
\end{align}
このように $\mathbb{I}, X, Z, H$ は「2回ユニタリ発展させると元に戻る」という性質があります。
また、$R_\theta$ の逆行列は、
\begin{align}
R_\theta^{-1} = \TwoTwo{1}{0}{0}{e^{i\theta}}^{-1} = \TwoTwo{1}{0}{0}{e^{-i\theta}} = R_{-\theta}
\end{align}
となります。
$R_\theta$ が「複素平面上で原点を中心に反時計回りに $\theta$ ラジアン回転する」のに対し、逆行列$R_\theta^{-1}$ は「複素平面上で原点を中心に時計回りに $\theta$ ラジアン回転する」という操作になります。
測定
行列の話が延々と続き、飽きてきた頃ですよね。そろそろ測定の話をしましょう。
第1回でも説明したように、量子状態を測定することで計算結果を把握することができます。そのため、計算した後は基本的に測定を行うことになります。
また、測定後の量子状態は $\Ket{0}$ か $\Ket{1}$ になることに注意が必要です。
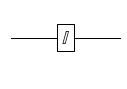
「測定」を表現する量子ゲートの記法はいくつか種類があります。
下の方の速度メータのようなマークが多数派かと思いますが、このシリーズでは上の方の $M_Z$ で測定を表します。
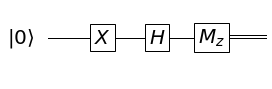
例えば、
- 量子ビットの初期値を $\Ket{0}$ とする。
- パウリ行列 $X$ でビット反転させる。
- アダマール行列 $H$ で重ね合わせ状態を作る。
- 測定する。
という計算を行う量子回路は次のようになります。
これを具体的に計算すると、次のようになります。
\begin{align}
HX\Ket{0} &= H\TwoTwo{0}{1}{1}{0}\TwoOne{1}{0} = H\TwoOne{0}{1} \\
&= \FracTwo\TwoTwo{1}{1}{1}{-1}\TwoOne{0}{1} = \FracTwo\TwoOne{1}{-1} \\
&= \FracTwo(\Ket{0}-\Ket{1})
\end{align}
そのため、$HX\Ket{0}$ を測定して $\Ket{0}$ を得る確率は $\left|\frac{1}{\sqrt{2}}\right|^2 = \frac{1}{2}$、$\Ket{1}$ を得る確率は $\left|\frac{-1}{\sqrt{2}}\right|^2 = \frac{1}{2}$ となります。
ここで例に挙げた量子回路は比較的シンプルなものですが、具体的な行列を考えた途端、計算が煩雑になったと感じますよね。
量子回路を見るたびにこのような行列計算を行うのは、正直言って大変です。
ただ、このような計算を何度か行っていると、行列計算をせずに量子ビットがどのように変化するか分かるようになってきます。例えば、「パウリ行列 $X$ はビット反転」といったように、行列計算をしなくても量子ビットの計算ができるようになってきます。
\begin{align}
X\Ket{0} &= \Ket{1} \\
X\Ket{1} &= \Ket{0} \\
\end{align}
こういう計算経験を積み重ねる事で、段々と複雑な量子回路での量子ビットの変化を、実際に行列計算することなく行えるようになると思います。
今回の例は1量子ビットなのでシンプルですが、今後はもっと複雑な量子回路が登場します。そのため、今回紹介した代表的な量子ゲートの計算には慣れておいた方が良いと思います。例えば、量子状態 $\alpha\Ket{0}+\beta\Ket{0}$ が各量子ゲートでどのように変化するのか、計算してみるのは良い練習になると思います。
次回の内容
第1回と第2回では、量子ビットや量子回路の説明を行いました。基本的な考え方はある程度説明しましたが、やはり1量子ビットの世界ではできることが限られています。
次回はもう少し範囲を広げて、2量子ビットの世界について説明します。
行列の計算はもう少し複雑になりますが、計算規則が分かれば大丈夫です。まずは、1量子ビットの場合をしっかり理解しておきましょう。
それではまた、次回もよろしくお願いします。