\newcommand{\OneTwo}[2]{\left(\begin{array}{cc} #1 & #2 \end{array} \right)}
\newcommand{\TwoOne}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array} \right)}
\newcommand{\TwoTwo}[4]{\left(\begin{array}{cc} #1 & #2 \\ #3 & #4 \end{array} \right)}
\newcommand{\ThreeOne}[3]{\left(\begin{array}{c} #1 \\ #2 \\ #3 \end{array} \right)}
\newcommand{\OneFour}[4]{\left(\begin{array}{cccc} #1 & #2 & #3 & #4 \end{array} \right)}
\newcommand{\FourOne}[4]{\left(\begin{array}{c} #1 \\ #2 \\ #3 \\ #4 \end{array} \right)}
\newcommand{\Bra}[1]{\mathinner{\left\langle{#1}\right|}}
\newcommand{\Ket}[1]{\left|{#1}\right\rangle}
\newcommand{\matI}[0]{\TwoTwo{1}{0}{0}{1}}
\newcommand{\matX}[0]{\TwoTwo{0}{1}{1}{0}}
\newcommand{\matY}[0]{\TwoTwo{0}{-i}{i}{0}}
\newcommand{\matZ}[0]{\TwoTwo{1}{0}{0}{-1}}
こんにちは、@snuffkinです。
ここ数年、量子コンピュータを使った、古典データに対する機械学習の研究が進んでいます。
古典データを量子コンピュータで扱うには、量子状態に符号化する必要がありますが、符号化について具体的に書いてある記事は少ないように思います。そこで、この記事では、古典データを量子状態に符号化する方法を紹介します。。。
と、最初は考えていたのですが、12/3のアドベントカレンダーの記事
多量子ビット状態の可視化(多次元ブロッホ球)
https://electrodynamics.hatenablog.com/entry/2020/11/29/235551
で使っている手法が面白かったので、予定を変更し、この手法を使ってブロッホ球を幾何学的に理解する方法について紹介します。
1量子ビットの量子状態やゲート操作を、ブロッホ球で幾何学的にイメージできるようにするのが、ゴールです。
前提
この記事では、1量子ビットのみ扱います。
状態ベクトルやブラケット記法は知っている前提で、特に説明しません。
単位行列$I$、1量子ビットのゲート操作によく使われるパウリ行列$X,Y,Z$は次の形をした行列のことです。
$$I=\matI, X=\matX, Y=\matY, Z=\matZ$$
慣れるまでは、パウリ行列$Y$のマイナスがどの成分につくのかすぐに忘れてしまいますが、慣れましょう😅
状態ベクトルでブロッホ球を理解するの、無理じゃありません?
たいていの入門記事では、量子状態は状態ベクトルで表現されています。
\begin{align}
\Ket{0} &= \TwoOne{1}{0} \\
\Ket{1} &= \TwoOne{0}{1} \\
\end{align}
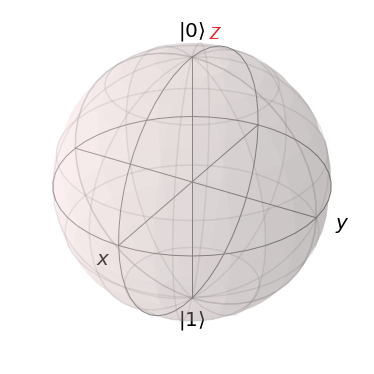
これをブロッホ球で表現すると、次のようになります。
原点を中心とする3次元球面の上の点$(0,0,1)$に$\Ket{0}$があり、$(0,0,-1)$に$\Ket{1}$があります。
まず、ここからして訳が分からないですよね。
だって、
$$-(0,0,1) = (0,0,-1)$$
なんだから、
$$-\Ket{0} = \Ket{1}$$
となるのを期待するのが、自然な発想だと思うんですよね。でも、そうはならない。
量子コンピュータを学び始めたとき、何でこんなことをするのか意味が分からなくてつまづきました。
さらに、パウリ行列
$$X=\matX$$
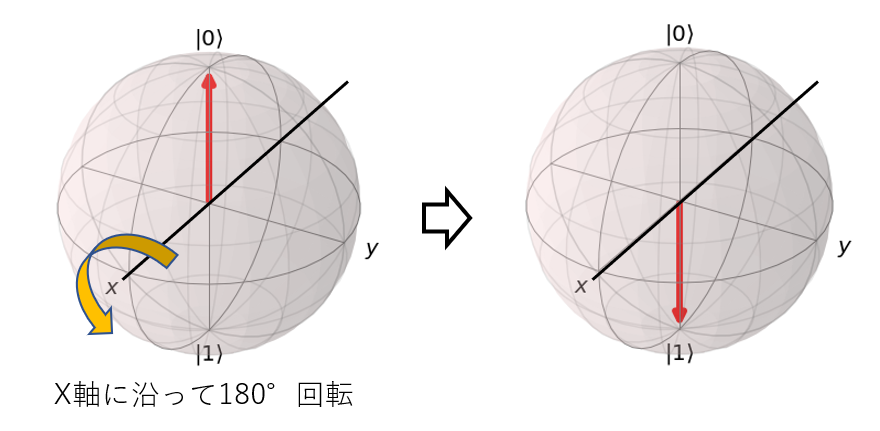
で$\Ket{0},\Ket{1}$をゲート操作させると$X\Ket{0}=\Ket{1},X\Ket{1}=\Ket{0}$となりますが、この$X$がブロッホ球の$x$軸に沿って180°回転させる操作だというのです。
パウリ行列$X$をいくら眺めても、これが$x$軸に沿って180°回転しているとはイメージできませんでした。。。
えっ、何このブロッホ球っての、ちっとも美味しくない。
学び始めの私は、そう思いました。
球面座標系の扱いに慣れている人は違った印象を持つのかもしれませんが、物理のバックグラウンドがない大半の入門者は訳が分からないのではないでしょうか。
状態ベクトルによる表現と、素朴な座標表示によるブロッホ球表現は、相性が悪いよう思います。
密度行列で表現する
実は美味しく食べる方法があるのですが、下ごしらえが必要です。材料は状態ベクトルではなく、密度行列を使います。
密度行列をざっくりいうと、ケット記号で表した量子状態を、「ケット$\times$ブラ」にしたものです。
たとえば、状態ベクトル$\Ket{0}, \Ket{1}$を密度行列で表現すると、次のようになります。
\begin{align}
\Ket{0}\Bra{0} = \TwoOne{1}{0} \OneTwo{1}{0} = \TwoTwo{1}{0}{0}{0} \\
\Ket{1}\Bra{1} = \TwoOne{0}{1} \OneTwo{0}{1} = \TwoTwo{0}{0}{0}{1} \\
\end{align}
1量子ビットの状態ベクトルは2次元「ベクトル」だったのに対し、密度行列は2次の正方「行列」になります。
また、密度行列はエルミート行列になります。($U$が密度行列だとすると、$U^\dagger = U$となります)
エルミート行列のパウリ行列展開とその座標成分(2)
https://electrodynamics.hatenablog.com/entry/2018/12/01/233744
上記の記事でも紹介されているように、エルミート行列にはきれいな性質があり、パウリ行列(と単位行列)を基底として、実数係数の線形結合で書くことができます。
たとえば、$\Ket{0}\Bra{0}と\Ket{1}\Bra{1}$は次のような線形結合で書けます(確かめてみてください)。
\begin{align}
\Ket{0}\Bra{0} = \TwoTwo{1}{0}{0}{0} = \frac{1}{2}\cdot I + 0\cdot X + 0\cdot Y + \frac{1}{2}\cdot Z \\
\Ket{1}\Bra{1} = \TwoTwo{0}{0}{0}{1} = \frac{1}{2}\cdot I + 0\cdot X + 0\cdot Y + \frac{-1}{2}\cdot Z \\
\end{align}
座標表現の基底を変えてみる
さきほど書いたように、$\Ket{0}$の座標をブロッホ球で表現すると$(0,0,1)$となります。これを縦ベクトルで書くと、
$$\ThreeOne{0}{0}{1}$$
です。普段あまり気にしていないと思いますが、このベクトル表現は基底に依存しています。具体的には、基底が単位ベクトル
$$ \ThreeOne{1}{0}{0}, \ThreeOne{0}{1}{0}, \ThreeOne{0}{0}{1}$$
であることを暗黙の前提にしています。実際、単位ベクトルを基底として
$$\ThreeOne{0}{0}{1} = \color{red}{0}\cdot \ThreeOne{1}{0}{0} + \color{red}{0}\cdot \ThreeOne{0}{1}{0} + \color{red}{1}\cdot \ThreeOne{0}{0}{1}$$
と書くことができ、線形結合の係数$0, 0, 1$を並べたものが$(0,0,1)$になるわけです。
これは自明な例なので面白くないかもしれませんが、このあと、自明でないケースを説明します。混乱したらここに帰ってきましょう。
さて、この記事の密度行列の節でも書いたように、量子状態$\Ket{0}\Bra{0}, \Ket{1}\Bra{1}$は次のように書けました。
\begin{align}
\Ket{0}\Bra{0} &= \TwoTwo{1}{0}{0}{0} = \color{red}{\frac{1}{2}}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{\frac{1}{2}}\cdot Z \\
\Ket{1}\Bra{1} &= \TwoTwo{0}{0}{0}{1} = \color{red}{\frac{1}{2}}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{\frac{-1}{2}}\cdot Z \\
\end{align}
したがって、パウリ行列(と単位行列)を基底とした線形結合の係数$\frac{1}{2}, 0, 0, \pm\frac{1}{2}$を縦ベクトルとして並べることで次のように書けます。
\begin{align}
\Ket{0}\Bra{0} &= \frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{1}}_{HS} \\
\Ket{1}\Bra{1} &= \frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{-1}}_{HS} \\
\end{align}
単位ベクトルを基底とする表示と区別するため、パウリ行列(と単位行列)を基底とした表示の右下に「$HS$」と書きました。
縦ベクトルの一部を赤く書いたのには意味があり、実はこの部分がブロッホ球の座標に対応しています。
状態ベクトルを使った場合は、ブロッホ球の座標に対応させるために$\cos$関数や$\sin$関数を使って変換していましたが、この表示を使うとブロッホ球の座標と自然に対応します。
ブロッホ球上の座標$(x,y,z)$に対応する密度行列は、次のように書けます。
$$\frac{1}{2}\FourOne{1}{x}{y}{z}_{HS}$$
「$HS$」による座標表示の中に$x,y,z$が自然に登場しました。$\cos$関数や$\sin$関数を使って変換する必要もないですし、これは扱いやすそうです。
ゲート操作を表現行列で表す
抽象的な関数である線形演算子を、行列の形で表したものを表現行列といいます。
ゲート操作を表現行列で表したいのですが、まずは簡単な例で理解するため、状態ベクトルで説明します。
ゲート操作に対応するユニタリ行列を$U$とし、これを状態ベクトル$\Ket{\varphi}$に適用すると、量子状態は$U\Ket{\varphi}$になります。この操作を線形演算子$f_U$だと考えると、$f_U(\Ket{\varphi}) = U\Ket{\varphi}$となります。
パウリ行列$X$の場合に、$\Ket{0}, \Ket{1}$がどうなるか計算してみます。
\begin{align}
f_X(\Ket{0}) &= X\Ket{0} = \Ket{1} = \color{red}{0}\cdot\Ket{0} + \color{red}{1}\cdot\Ket{1} \\
f_X(\Ket{1}) &= X\Ket{1} = \Ket{0} = \color{red}{1}\cdot\Ket{0} + \color{red}{0}\cdot\Ket{1} \\
\end{align}
この右辺のように、線形演算子により基底が何に写ったのか、基底の線形結合で書いてみます。これらの係数を行列として表現したものが、線形演算子の表現行列です。
この場合、線形演算子$f_X$の表現行列は
$$\TwoTwo{0}{1}{1}{0}$$
になります。パウリ行列$X$と一致しましたね。これは偶然ではなく、単位ベクトルを基底としているので、自明な結果に見えます。
さて、密度行列で表現した場合のゲート操作について、表現行列を求めてみましょう。
ゲート操作に対応するユニタリ行列を$U$とし、これを密度行列$\rho$に適用すると、量子状態は$U\rho U^\dagger$になります。この操作を線形演算子$\bar{f_U}$だと考えると、$\bar{f_U}(\rho) = U\rho U^\dagger$となります。
パウリ行列$X$の場合に、$\Ket{0}\Bra{0}, \Ket{1}\Bra{1}$がどうなるか計算してみます。基底はパウリ行列(と単位行列)で考えます。
\begin{align}
\bar{f_X}(\Ket{0}\Bra{0}) = X\Ket{0}\Bra{0}X^\dagger = \TwoTwo{0}{0}{0}{1} = \color{red}{\frac{1}{2}}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{\frac{-1}{2}}\cdot Z = \frac{1}{2}\FourOne{1}{0}{0}{-1}_{HS} = \Ket{1}\Bra{1} \\
\bar{f_X}(\Ket{1}\Bra{1}) = X\Ket{1}\Bra{1}X^\dagger = \TwoTwo{1}{0}{0}{0} = \color{red}{\frac{1}{2}}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{\frac{1}{2}}\cdot Z= \frac{1}{2}\FourOne{1}{0}{0}{1}_{HS} = \Ket{0}\Bra{0} \\
\end{align}
「座標表現の基底を変えてみる」で説明した「$HS$」の表示と一致しますね。
$\Ket{0}\Bra{0}$や$\Ket{1}\Bra{1}$を「$HS$」の表示に変えてみると、状況がもっとクリアになります。
\begin{align}
\bar{f_X}(\frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{1}}_{HS}) = \frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{-1}}_{HS} \\
\bar{f_X}(\frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{-1}}_{HS}) = \frac{1}{2}\FourOne{1}{\color{red}{0}}{\color{red}{0}}{\color{red}{1}}_{HS} \\
\end{align}
「$HS$」で縦ベクトル表示した赤字の座標を見ると、ゲート操作$X$により$(0,0,1) \leftrightarrow -(0,0,1)$と変わっており、符号が反転していますね。
「パウリ行列$X$の操作によって、$x$軸に沿って180°回転している!」と言いたいですが、まだ早いです。3次元球面の回転を特定するには3点必要となりますが、この例だと$(0,0,1)$と$(0,0,-1)$の2点しか分かっていません。たとえば$y$軸に沿って180°回転しても$(0,0,1) \leftrightarrow -(0,0,1)$と符号が反転します。
もう一息頑張って、ゴールを目指しましょう。
線形演算子を特徴付けるために表現行列を求めてみましょう。基底であるパウリ行列(と単位行列)が$\bar{f_X}$でどうなるか計算します。
(ちょっと面倒かとは思いますが、2次行列の計算を根気よくやってみましょう!)
\begin{align}
\bar{f_X}(I) &= XIX^\dagger = \cdots = I = \color{red}{1}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{0}\cdot Z = \FourOne{1}{0}{0}{0}_{HS} \\
\bar{f_X}(X) &= XXX^\dagger = \cdots = X = \color{red}{0}\cdot I + \color{red}{1}\cdot X + \color{red}{0}\cdot Y + \color{red}{0}\cdot Z = \FourOne{0}{1}{0}{0}_{HS} \\
\bar{f_X}(Y) &= XYX^\dagger = \cdots = -Y = \color{red}{0}\cdot I + \color{red}{0}\cdot X + \color{red}{-1}\cdot Y + \color{red}{0}\cdot Z = \FourOne{0}{0}{-1}{0}_{HS} \\
\bar{f_X}(Z) &= XZX^\dagger = \cdots = -Z = \color{red}{0}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{-1}\cdot Z = \FourOne{0}{0}{0}{-1}_{HS} \\
\end{align}
この線形結合の係数を列に並べた次の行列が$\bar{f_X}$の表現行列になります(基底を区別するため、行列の右下に「$HS$」と書きます)。
\begin{align}
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{array}
\right)_{HS}
\end{align}
出ました!
これが、パウリ行列$X$の「$HS$」での表現行列です。表現行列を使うと、ブロッホ球の座標$(x,y,z)$が写る先を次のように計算できます。
\begin{align}
\bar{f_X}(\frac{1}{2}\FourOne{1}{\color{red}{x}}{\color{red}{y}}{\color{red}{z}}_{HS}) =
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & -1 \\
\end{array}
\right)_{HS}
\cdot \frac{1}{2}\FourOne{1}{\color{red}{x}}{\color{red}{y}}{\color{red}{z}}_{HS} =
\frac{1}{2}\FourOne{1}{\color{red}{x}}{\color{red}{-y}}{\color{red}{-z}}_{HS}
\end{align}
この結果から、パウリ行列$X$により$(x,y,z)$が$(x,-y,-z)$に写ることが分かります。$x$座標は変わらず、$y$座標と$z$座標の符号が反転しています。これは$x$軸に沿って180°回転する操作と一致しています。
こうしてみると、ブロッホ球での操作を自然な形で幾何学的にイメージできるのではないでしょうか。
このような表現をHilbert-Schmidt表現と呼びます(文献によっては呼び方が異なる場合もあります)。「$HS$」と書いたのは、Hilbert-Schmidt表現を意図しています。
パウリ行列X以外の表現行列は?
ちなみに、同じように計算すると、次のことも分かります。(手を動かしてみましょう)
\begin{align}
パウリ行列Yの表現行列 &=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & -1 \\
\end{array}
\right)_{HS} \\
パウリ行列Zの表現行列 &=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}
\right)_{HS} \\
アダマール行列Hの表現行列 &=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & -1 & 0 \\
0 & 1 & 0 & 0 \\
\end{array}
\right)_{HS} \\
\end{align}
パウリ行列$Y$は$y$軸に沿った180°回転、パウリ行列$Z$は$z$軸に沿った180°回転、というのが分かりやすいですね。また、おまけですが、パウリ行列$Y$の表現行列が対称行列になっているので、マイナスがどの成分につくのか覚えずにすみます。
アダマール行列$H$は$x$座標と$z$座標が入れ替わって、$y$座標の符号が反転しています。
このような表現を考えると、ブロッホ球の操作を幾何学的にイメージでき、美味しく頂けるのではないでしょうか。
量子的な操作を表すには、さまざまな表現があります
状態ベクトルや、Hilbert-Schmidt表現以外にも、量子的な操作に関する様々な表現方法があります。
表現方法によって特徴があるので、目的を達成するために最適な表現を使うのが良いと思います。
Hilbert-Schmidt表現の長所としては、次のようなものが挙げられます。
- ゲート操作の表現行列の成分は実数(状態ベクトルの場合は行列の成分は複素数でした)
- ブロッホ球の操作がイメージしやすい
- ゲート操作に対応する行列が一意に定まる(状態ベクトルの場合、$X$と$-X$は行列としては異なるが、位相が異なるだけなのでゲート操作としては同じ。そのため、ゲート操作と行列が一意に対応しない)
逆に次のような短所もあります。
- 状態ベクトルと比べると、表現行列のサイズが大きくなってしまう(状態ベクトルのパウリ行列$X$は2次正方行列でしたが、$\bar{f_X}$の表現行列は4次正方行列になります)
- テンソル積の扱いが、ちょっと面倒(2量子ビット以上の表現行列を考えるときに遭遇します)
いかがだったでしょうか。
下ごしらえは必要でしたが、ブロッホ球をイメージしやすいHilbert-Schmidt表現を使うことで、幾何学的に理解しやすくなったと思います。
今日からブロッホ球を美味しく頂けますね😄