Hypergraph Neural Network[1]を読んだのでメモを残します．
[1] Feng, Yifan and You, Haoxuan and Zhang, Zizhao and Ji, Rongrong and Gao, Yue, Hypergraph neural networks．Proceedings of the AAAI, 2019
簡潔にまとめると
- Hypergraphに適用できるようにGCNを拡張したHGNNを提案する．
- Hyperedgeを経由してノード間を接続し，伝搬を行っている．
この論文を読む際に必要な前提知識
詳しくまとめると
- グラフによっては，2つのノードだけでなく，複数のノードが繋がっていることもある(Hypergraph)．
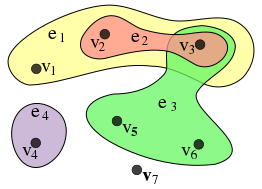
(wikipedia ハイパーグラフより引用)
- GCNはHypergraphを扱えない
-
Hypergraphはコンピュータビジョンの分野で使用されているが，既存の手法は計算コストが高い． 下の図では似ている画像をクラスタリングしてHypergraphを作成している．
メモ：論文では「計算コストが高い」と述べられているが，その理由は述べられていない．そこで，引用している文献を見たところ，クラスタ内の画像について総当たりで画像ペアを近づけるように学習を行っていた．この方法だと確かに計算コストは高い．
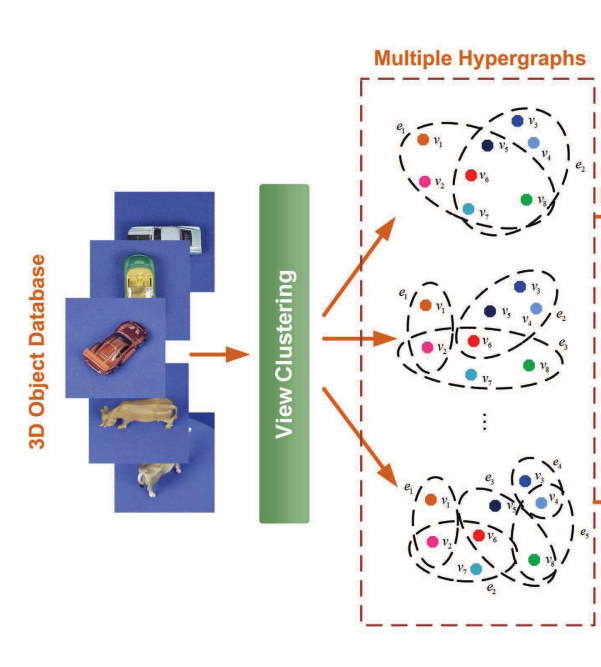
(3-D Object Retrieval and Recognition With Hypergraph Analysisより引用)
-
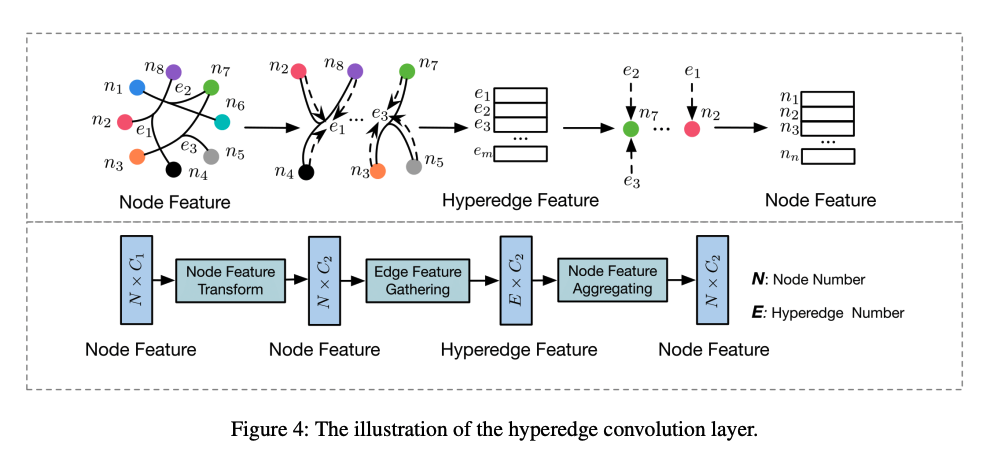
提案手法のHGNNではHypergraphを効率的に扱うことができる
$l$層目における更新式は以下の通り．
$$
X^{(l+1)} = \sigma\left(\color{orange}{D_v^{-\frac{1}{2}} H W D_e^{-1} H^\top D_v^{-\frac{1}{2}}} X^{(l)} \Theta^{(l)}\right)
$$
参考：GCNの更新式
$$
X^{(l+1)} = \sigma\left(\color{orange}{\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}} X^{(l)} \Theta^{(l)}\right),\quad \text{ただし }
\tilde{A} = A + I
$$
HGNNの更新式
この式の意味を以下に記述します．（導出は論文を参照してください，GCNの論文の2章を踏まえるとわかりやすいかと思います．）
まず，変数についてまとめます．
\begin{align}
&N \cdots \text{ノード数} \\
&E \cdots \text{エッジ数} \\
&d_l \cdots \text{$l$層目の特徴量の次元}\\
&X^{l} \in \mathbb{R}^{N \times d} \cdots \text{$l$層目の特徴量}\\
&D_v \in \mathbb{R}^{N \times N} \cdots \text{ノードに関する次数行列}\\
&\ \ \small \text{ただし，ノードの次数は，そのノードが含まれているエッジに関する重みの和で定義します}\\
&H \in \mathbb{R}^{N \times E} \cdots \text{接続行列（後述）}\\
&W \in \mathbb{R}^{E \times E} \cdots \text{エッジの重みを対角成分に取った行列}\\
&D_e \in \mathbb{R}^{E \times E} \cdots \text{エッジに関する次数行列}\\
&\ \ \small \text{ただし，エッジの次数は，繋げているノードの数で定義します}\\
&\Theta \in \mathbb{R}^{d_l \times d_{l+1}} \cdots \text{パラメータ行列}\\
&\sigma \cdots \text{活性化関数}\\
\end{align}
次に，数式についての詳細を見ていきます．
$$
X^{(l+1)} = \sigma\left(D_v^{-\frac{1}{2}} H W D_e^{-1} H^\top D_v^{-\frac{1}{2}} X^{(l)} \Theta^{(l)}\right)
$$
まず，簡単なところから．
$$
X^{(l+1)} = \sigma\left(\color{red}{D_v^{-\frac{1}{2}}} H \color{blue}{W} \color{red}{D_e^{-1}} H^\top \color{red}{D_v^{-\frac{1}{2}}} X^{(l)} \Theta^{(l)}\right)
$$
赤色の部分は，GCNにおける$\color{red}{\tilde{D}^{-\frac{1}{2}}} \tilde{A} \color{red}{\tilde{D}^{-\frac{1}{2}}}$と同様の役割です．
ただし，HGNNでは，1つのエッジが複数のノードと繋がるため，エッジについても調整を行っています．つまり，たくさんのノードを繋げているエッジの重要度を低く，少しのノードを繋げているエッジの重要度を高くしています．
青色の$W$でエッジの重みを取り入れています．
残ったところについて説明します．ここがメインです．
$$
X^{(l+1)} = \sigma\left(D_v^{-\frac{1}{2}} \color{red}{H} W D_e^{-1} \color{red}{H^\top }D_v^{-\frac{1}{2}}X^{(l)} \Theta^{(l)}\right)
$$
見やすいように取り出しましょう．
$$
\color{red}{H} \color{red}{H^\top }
$$
この計算がHGNNのポイントです．
まず，接続行列$H \in \mathbb{R}^{N \times E}$は，ノード$v_i$がエッジ$e_j$によって繋がれているとき，$H_{ij} = 1$とすることで得られる行列です．
$HH^\top$によって，Hyperedgeを経由してノード同士を繋ぐことができます．
ここから具体例で見てみます．
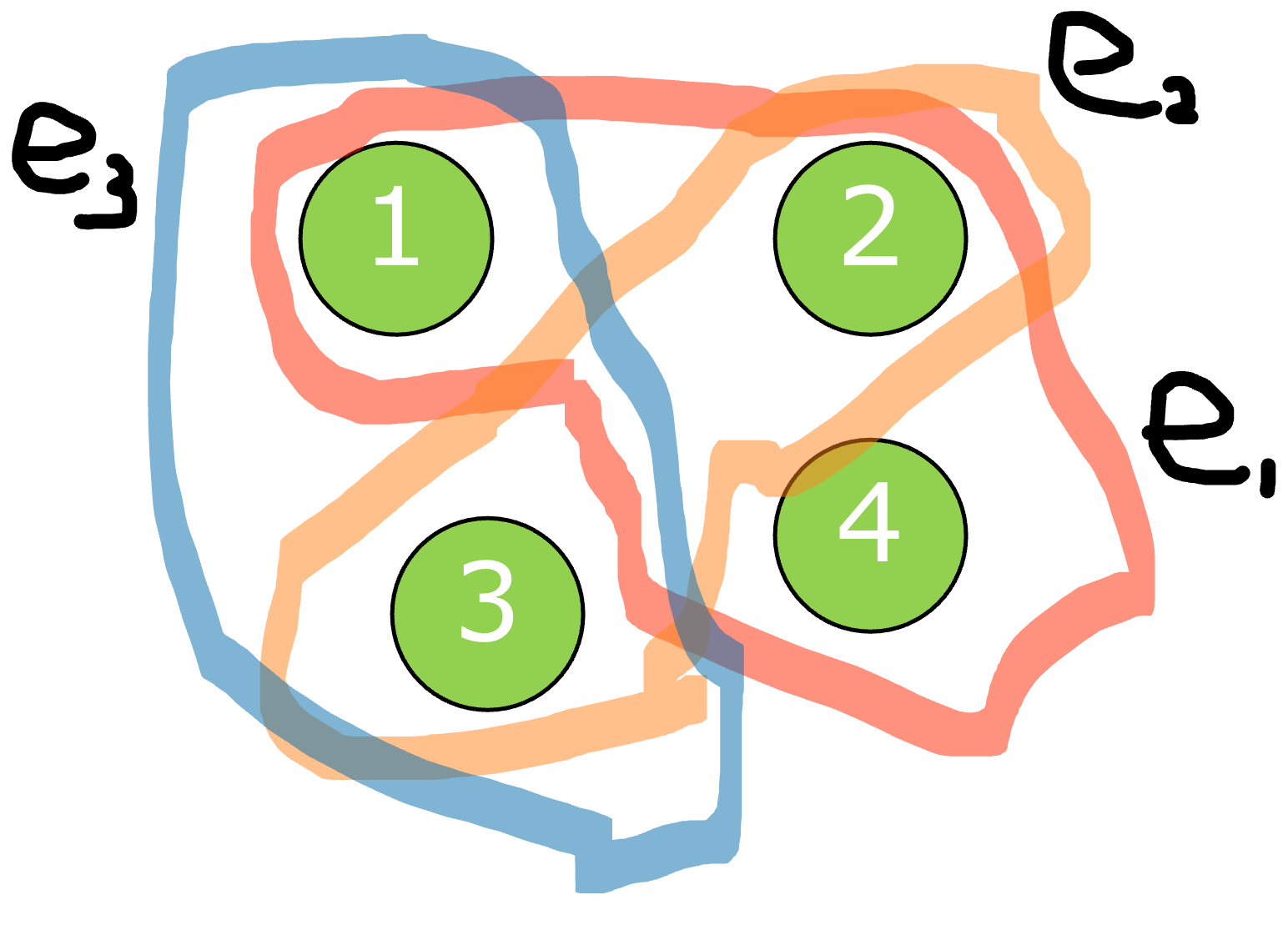
$H$
| $e_1$ | $e_2$ | $e_3$ | |
|---|---|---|---|
| $v_1$ | 1 | 0 | 1 |
| $v_2$ | 1 | 1 | 0 |
| $v_3$ | 0 | 1 | 1 |
| $v_4$ | 1 | 0 | 0 |
この例について
$HH^\top$を計算してみましょう．
\begin{pmatrix}
1 & 0 & 1 \\
1 & 1 & 0 \\
0 & 1 & 1 \\
1 & 0 & 0
\end{pmatrix}
\times
\begin{pmatrix}
1 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 \\
1 & 0 & 1 & 0
\end{pmatrix}
=
\begin{pmatrix}
2 & 1 & 1 & 1 \\
1 & 2 & 1 & 1 \\
1 & 1 & 2 & 0 \\
1 & 1 & 0 & 1
\end{pmatrix}
$HH^\top$
| $v_1$ | $v_2$ | $v_3$ | $v_4$ | |
|---|---|---|---|---|
| $v_1$ | 2 | 1 | 1 | 1 |
| $v_2$ | 1 | 2 | 1 | 1 |
| $v_3$ | 1 | 1 | 2 | 0 |
| $v_4$ | 1 | 1 | 0 | 1 |
$HH^\top$によって，Hyperedgeを経由してノード同士を繋がっていることが確認できます．例えば，ノード3は$e_1$と$e_2$によってノード1，2と繋がってます．
以上をまとめると，
HGNNは，エッジの重みと次数を考慮しつつ，Hyperedgeを経由してノード間を繋いでGCNに入力する手法と言えます．
この記事は以上です．