ABC206 B, C, D by Python3

ABC206
https://atcoder.jp/contests/abc206

B - Savings

$k$日後の貯金額は, $1 + 2 + 3 + ... + k = \sum_{i=1}^k i = \frac{k(k+1)}{1}$である.

よって, $\frac{k(k+1)}{2} \geq N $となる最小のkを求めれば良い.

さらにこの$f(k) = \frac{k(k+1)}{2}$は単調増加である.

これは前回のABC205-D の二分探索と同じで, 条件を満たす最小のindexを求める問題になる.

N = int(input())

# k日後の貯金金額
def f(k):
  return (k+1) * k // 2

# 二分探索
left = 0
right = 10**9 + 1
while left - right > 1:
  mid = (left + right) // 2
  if f(mid) >= N:
    right = mid
  else:
    left = mid

print(right)

C - Swappable

$1 \leq i \leq N$という条件は一旦おいておく.

$A_i \neq A_j$となるものを数えるのは大変なので, 全体から($A_i = A_j$となる個数) をひいて求める.

$A_i = A_j$となるものの個数は, PythonのCounterを使えば良さそう.

このようにして求めると, $(i,j)$と$(j,i)$がそれぞれ1回ずつカウントされることになるので, $1\leq i < j \leq N$の条件を思い出すと, これはどちらか一方のみカウントするという意味になるので, 最後に2で割る.

from collections import Counter
N = int(input())
A = list(map(int, input().split()))

cnt = Counter(A)

ans = 0
for i in range(N):
  ans += (N - cnt[A[i]])
print(ans // 2)

D - KAIBUNsyo

以下の説明と公式の解説, 両方読むとわかりやすいかもしれない.

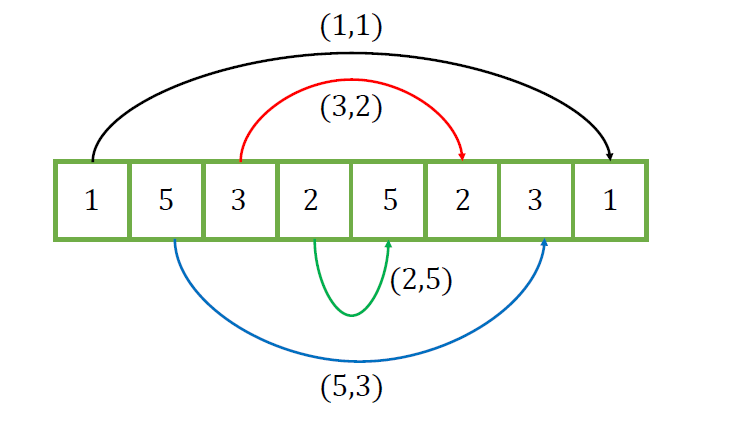
$A_i$に対して, $A_{N-i-1}$を$A_i$の反対側と呼ぶことにする.

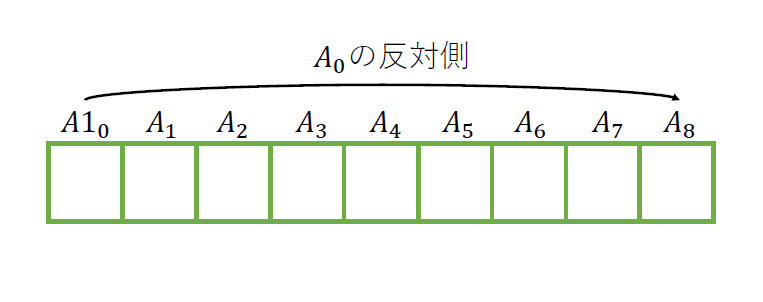
回分である条件は, 全ての$i$について$A_i$と$A_i$の反対側が同じ値になれば良い.
この条件は, $A_i$と$A_i$の反対側についてのみ考えれば良い. つまり, $A_i$と$A_j$($\neq A_iの反対側$)についてこれらの値が同じかどうかは考えなくて良い.

しかしながら今回の問題では, ある$A_i$の値を変える事によって, その反対側以外の要素にも変化を及ぼすため, 考えがややこしくなる.

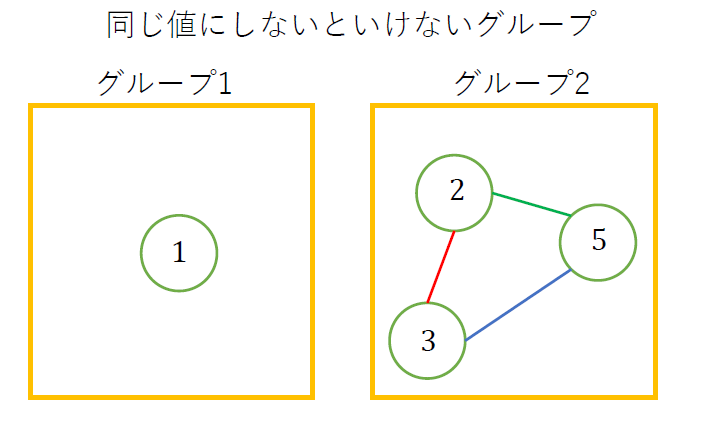
そこで, (同じ値にしなければならない$A$の要素)をまとまりとして考える.
ここで明らかに言えることは, $A_i$と$A_i$の反対側は必ず同じまとまりに属する.

この他に, ある$A_j$が$A_i$ or $A_i$の反対側と同じ値なら, この$A_j$も$A_i$と同じまとまりに属することになる.

具体例

$N=8, A = [1, 5, 3, 2, 5, 2, 3, 1]$

この上の対応関係から, 必要な塊をグラフで表すと

まとまりから答えを計算する

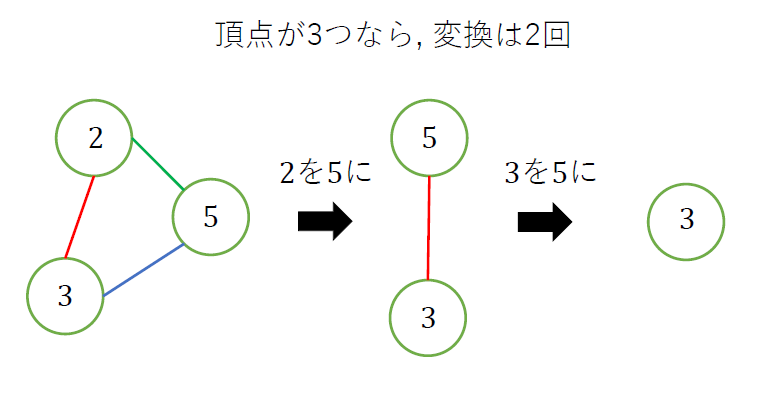
同じまとまりの頂点数（値の異なる$A_i$の数）が$k$個あるとする.
この$k$個の異なる数字を全て同じ数字にしないといけない. これにかかる個数はどう頑張っても$k-1$回なので, 1つのグループに対して最小$k-1$回の変換が必要になる.

よって, それぞれの塊に対して, $|塊の頂点数|-1$の総和が答えとなる.

UnionFindTree

これらを簡単に実現するデータ構造として, UnionFindTreeがあります.
UnionFindTreeは簡単に言えば, 集合を共通部分を持たない素集合に分割した状態でデータを持っておく構造です.

これの解説はしないので各自調べてください.

class UnionFindTree:
  def __init__(self, n):
    self.parents = [-1] * (n+1)
  def find(self, v):
    if self.parents[v] < 0:
      return v
    else:
      self.parents[v] = self.find(self.parents[v])
      return self.find(self.parents[v])

  def same_check(self, u, v):
    return self.find(u) == self.find(v)

  # ノードvが属する連結成分の個数を返す
  def size(self, v):
    return -1 * self.parents[self.find(v)]

  def union(self, u, v):
    u = self.find(u)
    v = self.find(v)

    if (-1 * self.parents[u]) > (-1 * self.parents[v]):
      self.parents[u] += self.parents[v]
      self.parents[v] = u
    else:
      self.parents[v] += self.parents[u]
      self.parents[u] = v

解答例

N = int(input())
A = list(map(int, input().split()))

# 現れる可能性のある 1 <= Ai <= 2 * 10 **5 の範囲の頂点を作る
tree = UnionFindTree(10**6)

# N//2までやれば十分
for i in range(N//2):
  u,v = A[i], A[N - i - 1]
  # 同じ塊を作る操作
  if not tree.same_check(u, v):
    tree.union(u, v)

# 塊の個数の計算
ans = 0
for i in tree.parents:
  if i < 0:
    ans += (-1 * i) - 1
print(ans)