平均律じゃなくたっていいじゃない 〜2の12乗根は無理数だもの〜

この記事は 42 Tokyo Advent Calendar 2023 の 12日目の記事です。

12といえば、西洋音楽で 1オクターブに存在する半音の数ですよね！

ということで、今回は go言語で wave ファイルを生成しつつ、平均律以外の音律でも演奏できるようにしてみたいと思います。

WAV ファイル

RIFFベースの音声ファイルフォーマット。
非圧縮リニアパルス符号変調で符号化した音声の格納によく用いられる。
要するに音の波形をそのまま数値化したデータを格納している。

WAV ヘッダー

type WaveHeader struct {
	ckID_riff       [4]byte // "RIFF"
	ckSize_riff     uint32  // 以降のバイト数 // 36+len(data)
	formType        [4]byte // "WAVE"
	ckID_fmt        [4]byte // "fmt "
	ckSize_fmt      uint32  // 16
	wFormatTag      uint16  // フォーマットタイプ // PCM=1
	nChannels       uint16  // チャネル数 // MONO=1
	nSamplesPerSec  uint32  // サンプリング・レート
	nAvgBytesPerSec uint32  // 平均バイト数/秒
	nBlockAlign     uint16  // ブロック境界合せ // 1*16/8 = 2
	wBitsPerSample  uint16  // ビット数/サンプル // 16
	ckID_data       [4]byte // "data"
	ckSize_data     uint32  // 以降のバイト数 // len(data)
}

c言語なら little endian 環境で以下のように書けるところだが、

write(fd, &wave_header, sizeof(wave_header));

go言語で構造体を little endian で書き込むには、encoding/binary package を使う。

import "encoding/binary"

binary.Write(file, binary.LittleEndian, wave_header)

WaveHeader 構造体に適切な値を詰め込んでくれる関数を用意。

func to_bytes(s string) (arr [4]byte) {
	copy(arr[:], s)
	copy(arr[len(s):], "    ")
	return arr
}

func NewWaveHeader(nChannels uint16, samplesPerSec uint32, bitsPerSample uint16, nBlocks uint32) WaveHeader {
	const ckSize_riffHeader = 36
	const ckSize_fmt = 16
	nBlockAlign := uint32(nChannels * bitsPerSample / 8)
	return WaveHeader{
		ckID_riff:       to_bytes("RIFF"),
		ckSize_riff:     ckSize_riffHeader + nBlocks*nBlockAlign,
		formType:        to_bytes("WAVE"),
		ckID_fmt:        to_bytes("fmt "),
		ckSize_fmt:      ckSize_fmt,
		wFormatTag:      LPCM,
		nChannels:       nChannels,
		nSamplesPerSec:  samplesPerSec,
		nAvgBytesPerSec: samplesPerSec * nBlockAlign,
		nBlockAlign:     uint16(nBlockAlign),
		wBitsPerSample:  bitsPerSample,
		ckID_data:       to_bytes("data"),
		ckSize_data:     nBlocks * nBlockAlign,
	}
}

WAV データ

ヘッダーの後には、波形データ(PCM)を little endian で書き込んでいく。
今回はモノラル、16bit/サンプル、サンプルレート 48kHz でファイルを生成することにした。

const (
	LPCM = 1

	MONO   = 1
	STEREO = 2

	RATE = 48000
)

type Sample int16

func main() {
	file, _ := os.Create("sample.wav")
	defer file.Close()

	wave_header := NewWaveHeader(MONO, RATE, 16, uint32(n_samples))
	binary.Write(file, binary.LittleEndian, wave_header)
	wave_data := make([]Sample, 0, n_samples)
 // ...
	binary.Write(file, binary.LittleEndian, wave_data)
}

サイン波を鳴らしてみる

周波数 $f$ Hz の音波は $sin(2 \pi f t)$ で表すことができる。

type Note struct {
	freq []float64
	time float64
	vel  uint8
}
// ...
	const A = 440.0
    // ラの音 2秒間 mfの音量で
	note := Note{[]float64{A}, 2, 64} 
	n_samples := int(RATE * note.time)
	wave_data := make([]Sample, 0, n_samples)

	for i := 0; i < n_samples; i++ {
		sample := 0.0
		for _, freq := range note.freq {
			sample += math.Sin(freq*2*math.Pi*float64(i)/RATE)
		}
		sample = sample * float64(note.vel) * 256 / float64(len(note.freq))
		wave_data = append(wave_data, Sample(sample))
	}

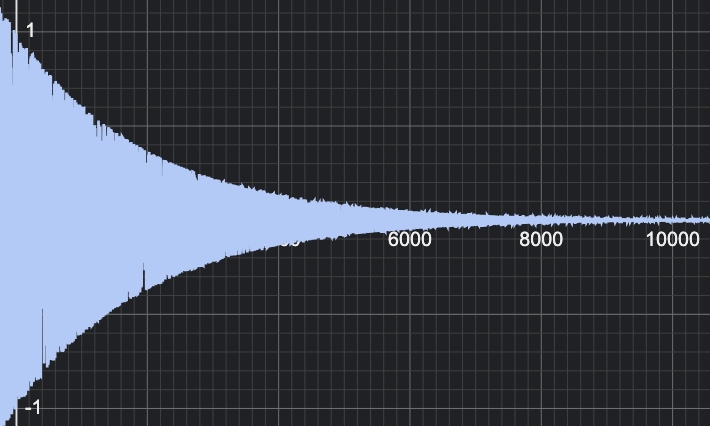
ただのサインカーブだとちょっと味気ないので、
$d^t* sin^3(2 \pi f t)$ としてみるとピアノの波形にやや近くなった。
$d$ は 1 よりわずかに小さい値で、減衰する速さを表す。

	const A = 440.0
	note := Note{[]float64{A}, 2, 64}
	n_samples := int(RATE * note.time)

	for i := 0; i < n_samples; i++ {
		sample := 0.0
		for _, freq := range note.freq {
			sample +=
				math.Pow(1-0.00005, float64(i)) *
					math.Pow(math.Sin(freq*2*math.Pi*float64(i)/RATE), 3)
		}
		sample = sample * float64(note.vel) * 256 / float64(len(note.freq))
		wave_data = append(wave_data, Sample(sample))
	}

早くも力尽きた

後で合成する関数を加筆します

音律

楽器をどのような周波数(比)で調律するかの決まり、といえばいいだろうか？

ヴァイオリンやチューバのようにフレットがない楽器は無段階で音高を変えられるが、
ピアノやオルガンのような鍵盤楽器は調律を頻繁に変更することが不可能なため、
音の響きと実用性をどのように調和させるか、おそらくこの世に楽器が現れたときからずっと議論されてきたはず。

いざ比較

go言語では定数同士の演算が正確なのがありがたい。
A4 = 基準のラ = 440.0 Hz をなるべく固定して比較してみる。

type FrequencyMap map[string]float64

const A = 440.0

平均律

$\sqrt[12] 2 = 2^{1/12}$ を半音とする音律。
移調が自由自在にできるが、完全八度(オクターブ)以外は有理数の比にならないため少しだけ濁ってしまう。
現代では最もよく使われている。現代の鍵盤楽器はほとんど全て平均律で調律されている。

var equal_map = FrequencyMap{
	"c":  A * math.Pow(2, 3/12) / 2,
	"c+": A * math.Pow(2, 4/12) / 2,
	"d-": A * math.Pow(2, 4/12) / 2,
	"d":  A * math.Pow(2, 5/12) / 2,
	"d+": A * math.Pow(2, 6/12) / 2,
	"e-": A * math.Pow(2, 6/12) / 2,
	"e":  A * math.Pow(2, 7/12) / 2,
	"f":  A * math.Pow(2, 8/12) / 2,
	"f+": A * math.Pow(2, 9/12) / 2,
	"g-": A * math.Pow(2, 9/12) / 2,
	"g":  A * math.Pow(2, 10/12) / 2,
	"g+": A * math.Pow(2, 11/12) / 2,
	"a-": A * math.Pow(2, 11/12) / 2,
	"a":  A * math.Pow(2, 0/12),
	"a+": A * math.Pow(2, 1/12),
	"b-": A * math.Pow(2, 1/12),
	"b":  A * math.Pow(2, 2/12),
}

ピタゴラス音律

$2:3$ を F-C C-G G-D D-A ... の 完全五度 = 7半音 とする音律。
3を12乗しても2の冪乗にはならないため、
平均律では完全に同音異名の音 (A♯ と B♭ など)の周波数がずれてしまう。
$ 2^{19} : 3^{12} = 524288:531441 \approx 1.01364 $ という比のことをピタゴラス・コンマと呼んだりする。

var pythagorean_map = FrequencyMap{
	"g-": A * 16384 / 19683,
	"d-": A * 4096 / 6561,
	"a-": A * 2048 / 2187,
	"e-": A * 512 / 729,
	"b-": A * 256 / 243,
	"f":  A * 64 / 81,
	"c":  A * 16 / 27,
	"g":  A * 8 / 9,
	"d":  A * 2 / 3,
	"a":  A * 1 / 1,
	"e":  A * 3 / 4,
	"b":  A * 9 / 8,
	"f+": A * 27 / 32,
	"c+": A * 81 / 128,
	"g+": A * 243 / 256,
	"d+": A * 729 / 1024,
	"a+": A * 2187 / 2048,
	"e+": A * 6561 / 8192,
}
var pythagorean_map_2 = FrequencyMap{
	"c":  A * 16 / 27,
	"c+": A * 81 / 128,
	"d-": A * 4096 / 6561,
	"d":  A * 2 / 3,
	"d+": A * 729 / 1024,
	"e-": A * 512 / 729,
	"e":  A * 3 / 4,
	"f":  A * 64 / 81,
	"f+": A * 27 / 32,
	"g-": A * 16384 / 19683,
	"g":  A * 8 / 9,
	"g+": A * 243 / 256,
	"a-": A * 2048 / 2187,
	"a":  A * 1 / 1,
	"a+": A * 2187 / 2048,
	"b-": A * 256 / 243,
	"b":  A * 9 / 8,
}

中全音律

$1: \sqrt[4]5$ を 完全五度 = 7半音、
$4:5$ を 長三度 = 4半音 とする音律。
ピタゴラス音律と同様に、5の4乗根を12乗しても2の冪乗にはならないのでずれてしまう。

var meantone_map = FrequencyMap{
	"g-": A * math.Pow(5, 3/4-3) * 32,
	"d-": A * math.Pow(5, 0/4-2) * 16,
	"a-": A * math.Pow(5, 1/4-2) * 16,
	"e-": A * math.Pow(5, 2/4-2) * 8,
	"b-": A * math.Pow(5, 3/4-2) * 8,
	"f":  A * math.Pow(5, 0/4-1) * 4,
	"c":  A * math.Pow(5, 1/4-1) * 4,
	"g":  A * math.Pow(5, 2/4-1) * 2,
	"d":  A * math.Pow(5, 3/4-1) * 2,
	"a":  A * math.Pow(5, 0/4+0) * 1,
	"e":  A * math.Pow(5, 1/4+0) / 2,
	"b":  A * math.Pow(5, 2/4+0) / 2,
	"f+": A * math.Pow(5, 3/4+0) / 4,
	"c+": A * math.Pow(5, 0/4+1) / 4,
	"g+": A * math.Pow(5, 1/4+1) / 8,
	"d+": A * math.Pow(5, 2/4+1) / 8,
	"a+": A * math.Pow(5, 3/4+1) / 16,
	"e+": A * math.Pow(5, 0/4+2) / 32,
}

純正律

2, 3, 5 の合成数の比で白鍵の音を表せる。
移調できないが和音が唸らず美しく響くのが特徴。

const C_just = A * 3 / 5

var just_map = FrequencyMap{
	"c": C_just * 1 / 1,
	"d": C_just * 9 / 8,
	"e": C_just * 5 / 4,
	"f": C_just * 4 / 3,
	"g": C_just * 3 / 2,
	"a": C_just * 5 / 3,
	"b": C_just * 15 / 8,
}

Vallotti

ピタゴラス音律に微調整を加えたもの。
白鍵間の完全五度は、ピタゴラスコンマを6等分ぶん短くして
$2 : 3/(531441 / 524288)^{1/6}$
それ以外は $2:3$ とする。

const pythagorean_comma = 531441.0 / 524288.0
const F_vallotti = 350.80926733010375

var vallotti_map = FrequencyMap{
	"f+": F_vallotti * 256 / 243,
	"g-": F_vallotti * 256 / 243,
	"c+": F_vallotti * 64 / 81,
	"d-": F_vallotti * 64 / 81,
	"g+": F_vallotti * 32 / 27,
	"a-": F_vallotti * 32 / 27,
	"d+": F_vallotti * 8 / 9,
	"e-": F_vallotti * 8 / 9,
	"a+": F_vallotti * 4 / 3,
	"b-": F_vallotti * 4 / 3,
	"f":  A * 64 / 81 * math.Pow(pythagorean_comma, 4/6.),
	"c":  A * 16 / 27 * math.Pow(pythagorean_comma, 3/6.),
	"g":  A * 8 / 9 * math.Pow(pythagorean_comma, 2/6.),
	"d":  A * 2 / 3 * math.Pow(pythagorean_comma, 1/6.),
	"a":  A * 1 / 1 * math.Pow(pythagorean_comma, 0/6.),
	"e":  A * 3 / 4 * math.Pow(pythagorean_comma, -1/6.),
	"b":  A * 9 / 8 * math.Pow(pythagorean_comma, -2/6.),
}

Werckmeister

4種類があり、ややこしいことに III 〜 VI とも I 〜 IV とも呼ばれることがある。

const C_werckmeister3 = 263.404

var werckmeister3_map = FrequencyMap{
	"c":  C_werckmeister3 * 1 / 1,
	"c+": C_werckmeister3 * 256 / 243,
	"d-": C_werckmeister3 * 256 / 243,
	"d":  C_werckmeister3 * 64 / 81 * math.Pow(2, 0.5),
	"d+": C_werckmeister3 * 32 / 27,
	"e-": C_werckmeister3 * 32 / 27,
	"e":  C_werckmeister3 * 256 / 243 * math.Pow(2, 0.25),
	"f":  C_werckmeister3 * 4 / 3,
	"f+": C_werckmeister3 * 1024 / 729,
	"g-": C_werckmeister3 * 1024 / 729,
	"g":  C_werckmeister3 * 8 / 9 * math.Pow(2, 0.75),
	"g+": C_werckmeister3 * 128 / 81,
	"a-": C_werckmeister3 * 128 / 81,
	"a":  C_werckmeister3 * 1024 / 729 * math.Pow(2, 0.25),
	"a+": C_werckmeister3 * 16 / 9,
	"b-": C_werckmeister3 * 16 / 9,
	"b":  C_werckmeister3 * 128 / 81 * math.Pow(2, 0.25),
}

// 割愛

実装

この記事を参考にできるかもしれません。できないかもしれません。

参考

終わりに

お読みいただきありがとうございます。
先人の並々ならぬ努力に涙が出てきました。波だけに。

12/13 は @hiroin さんが記事を書いてくださるのでお楽しみに！