備忘用メモ
NOTE
- 問題:https://leetcode.com/problems/longest-common-subsequence
- 解法:DP
- 注意:この問題はLongest Common Substring の問題で、Longest Common Subsequence ではないです。Subsequence の問題は下記で書いてます。
解法
Kadane's Algorithm とほぼ同じ考え方になる。
部分問題を定義する
まずは、DPなので部分問題に分解するが下記のように部分問題を定義する。
- 「文字列SのI番目の文字」と「文字列TのJ番目の文字」を含んでいる 最長共通部分列の長さ
(1: 「文字列SのI番目の文字」と「文字列TのJ番目の文字」を含んでいる、という条件のため、もしも「文字列SのI番目の文字」と「文字列TのJ番目の文字」が異なった場合、その時点で部分列共通ではなくなるため、長さは0になる。
(2:もしも「文字列SのI番目の文字」と「文字列TのJ番目の文字」が同じ場合は、1つ前の状態から長さを+1する
最終的な答えを取り出す
(3: 最終的な答えはdp全体の中から調べる必要がある。なぜなら、dp[I][J]が保持しているのは 「文字列SのI番目の文字」と「文字列TのJ番目の文字」を含んでいる 最長共通部分列の長さ だから。dpだからといってなにも考えずにdpの末尾の値を取り出しても、それは「最後の文字を含んだ最長共通部分列の長さ」になってしまう。
これらをもとに理解を優先して愚直に書くとこうなる。
func findLength(_ nums1: [Int], _ nums2: [Int]) -> Int {
var dp = [[Int]](repeating: [Int](repeating: 0, count: nums2.count+1), count: nums1.count+1)
for i in 1..<nums1.count+1 {
for j in 1..<nums2.count+1 {
let I = i-1, J = j-1;
if nums1[I] == nums2[J] {
dp[i][j] = dp[i-1][j-1] + 1 // (2) 1つ前の状態から長さを+1する
} else {
dp[i][j] = 0 // (1) 文字が違うので0になる
}
}
}
// (3) dp 全体から一番長い数値を取り出す
var maxSoFar = 0
for i in 0..<nums1.count+1 {
for j in 0..<nums2.count+1 {
maxSoFar = max(maxSoFar, dp[i][j])
}
}
return maxSoFar
}
ただ、冗長な記述ばっかりなのでもっとすっきりさせたい。
コード
最終的にこうなる。初期値は0なのでわざわざ0を代入する必要はなく、dp全体の中から最大値を取り出すのも緩和をしているループの中で合わせて行う。
func findLength(_ nums1: [Int], _ nums2: [Int]) -> Int {
var dp = [[Int]](repeating: [Int](repeating: 0, count: nums2.count+1), count: nums1.count+1)
var maxSoFar = 0
for i in 1..<nums1.count+1 {
for j in 1..<nums2.count+1 {
let I = i-1, J = j-1;
if nums1[I] != nums2[J] { continue }
dp[i][j] = dp[i-1][j-1] + 1
maxSoFar = max(maxSoFar, dp[i][j])
}
}
return maxSoFar
}
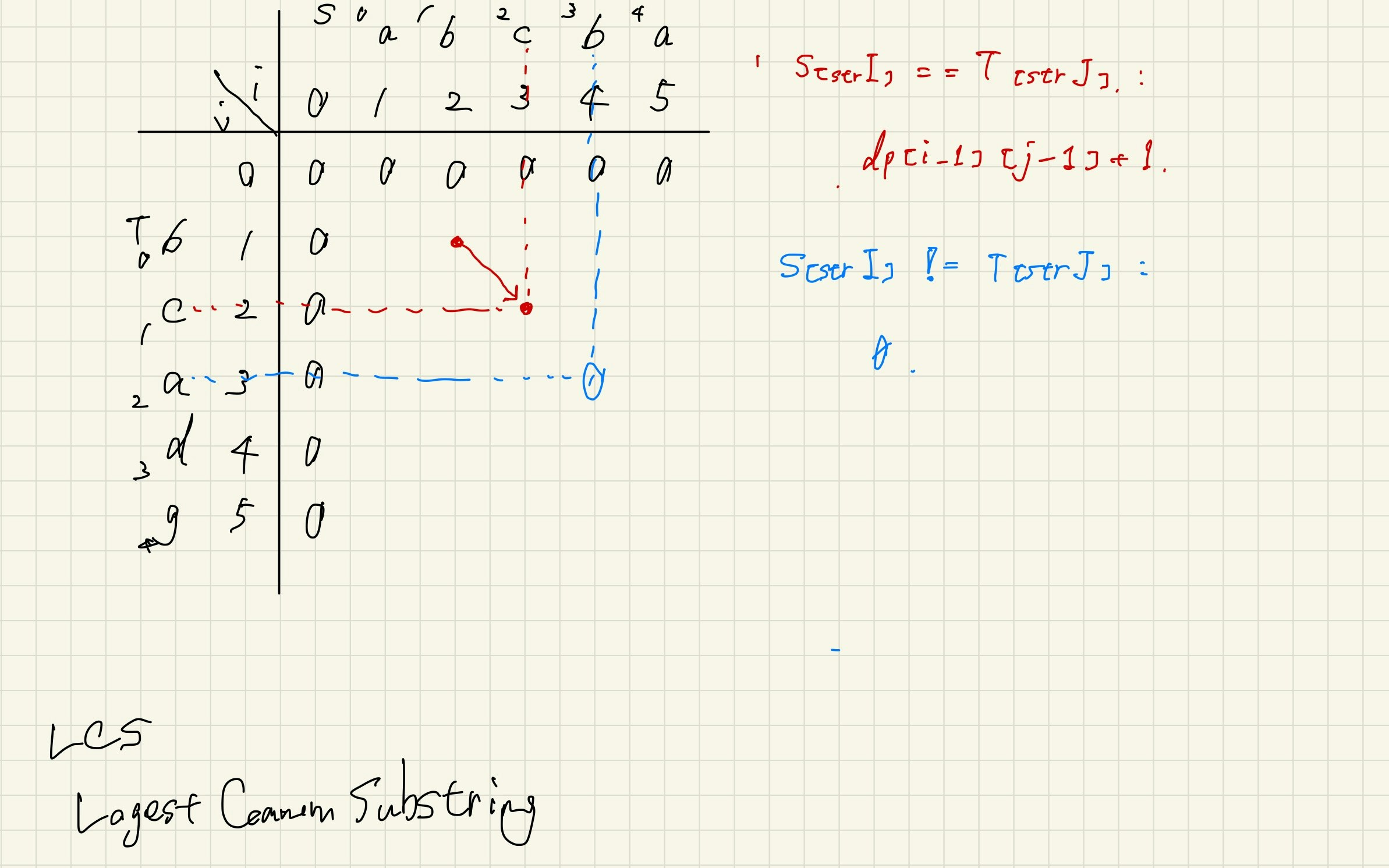
dp テーブル
dpのテーブルはこんな感じになる。
詰まったら
この問題で詰まった人は先にMaximum Substringをやるのがいいです。
Maximum Subarray の問題は1次元配列のDPだったのでより簡単だったが、今回の問題は2次元配列になる。今回の問題が詰まったら、先にMaximum Subarray やるほうがよりわかりやすいステップになると思う。