これは何
この記事は [eeic (東京大学工学部電気電子・電子情報工学科) Advent Calendar 2019] (https://qiita.com/advent-calendar/2019/eeic "") の 24 日目の記事です.
このアドベントカレンダーは一応はeeicで生きている人間の宣伝という体を取っているはずである, 多分ね. だからまあ, eeicに行くか迷うような人にやや参考になる, そんなeeicの総括について書こうと思った.
eeicでは2つの世界を見た. 離散と, 連続である. 情報から, 電子までである. その2つを境界として繋げる学問が電気系諸科目だったと言っても過言ではない. だから本来, 離散編・連続編・中間編みたいなものを書くべきだが, 面倒だった. まあ結局大抵どの研究室も手計算ではない計算か計測を命としてるんだ. 離散の世界に近似してるじゃないか. という事で離散の世界を纏めて電気系全体の纏めの近似としよう(連続から離散への近似という電子工学的思想を使った事を含めての総括).
雑な前置きが長くなったが, eeicで得た知識の内, 離散の知識っぽいものを纏める. 更にそれらが結局電子工学・電気工学っぽい他の科目でどう使ったけ?みたいなのを纏める. これには3つの意味がある.
- データ構造とアルゴリズムは情報系なら学んどけみたいな事言われてるけど結局工学的にどう役立つ訳???みたいな事を疑問に思ってる, 進学選択前のB1の私みたいな素直じゃない奴にそれっぽい事を伝える
- eeicの優秀なみんなに「いや〜〜こんな事にも使ったじゃんw」「弊研でもこういう実装する時にこの知識いるでw」みたいなのをコメント欄とかに書き足してもらう(私が思い出すのは情報系に偏りがちなので出来ればバランスを取って欲しい)→こういうの興味ある奴と研究室がマッチング出来て嬉しい!w
- 思い出すシリーズになって懐かしい
私の就活の為の勉強になる
注意としては, あまりデータ構造とアルゴリズムの内実は説明せず, 概念だけを伝える. ググる時の検索用単語を集めた単語集みたいなノリ. リストはソート出来ます, ヒープはヒープソートに使います, みたいな. 雑に思い出して書くので間違えてたら教えて下さい.
メジャーなデータ構造一覧
所詮全部グラフなのだと考えると楽になる. こんなのを作った. 多分そこら辺の競プロ資料にあるようなものはほぼ含めたはずだ. 矢印は制約を加えた部分集合くらいの意味である.
(小学校でやる四角形の分類みたいですね.)
具体的にどういう制約を加えているかは長いのでここにまとめます.
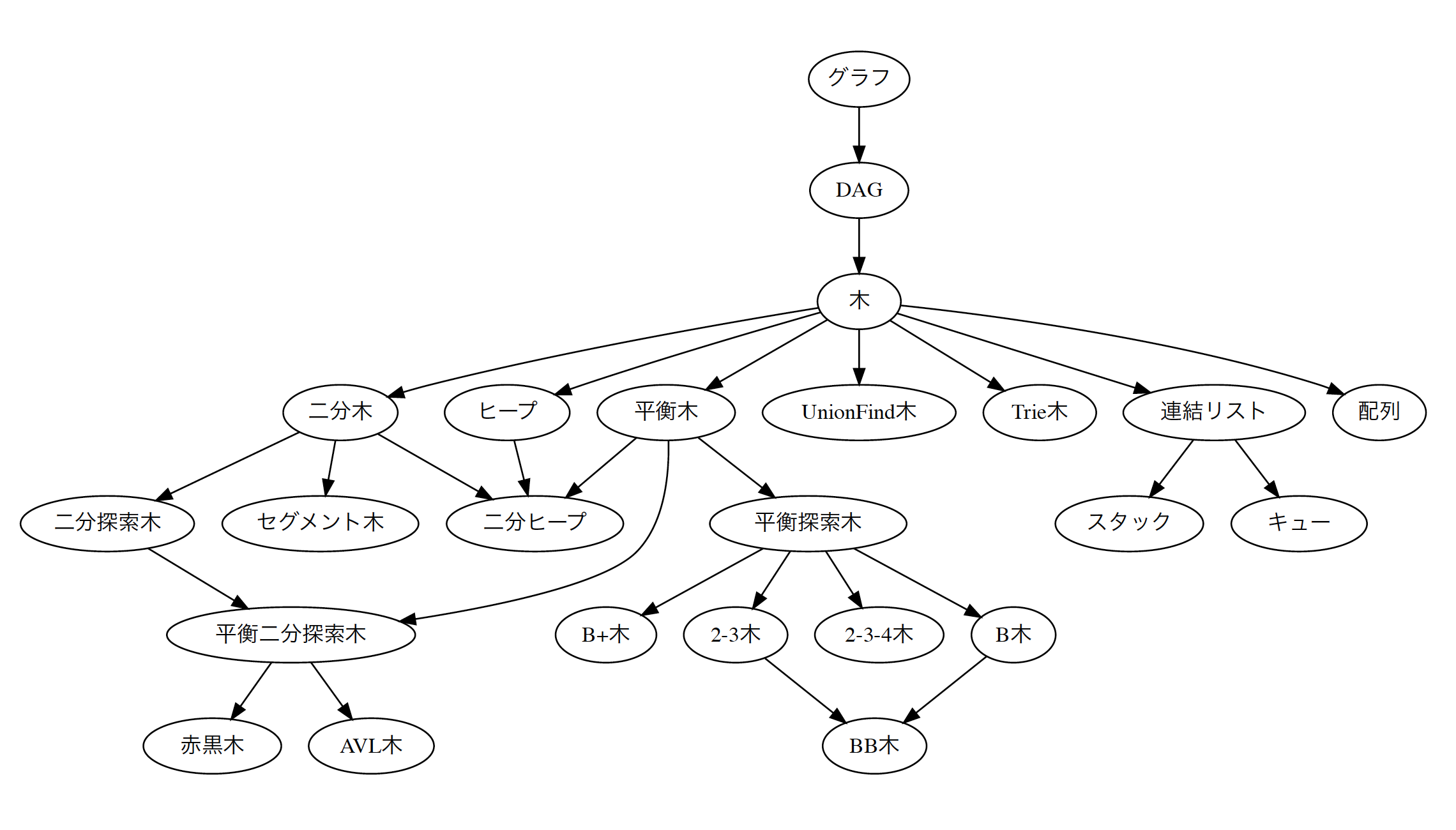
さて, 「この」グラフは分類すると, ど〜〜〜れだ??(DAGですね)
データ構造の応用
上にあるデータ構造から纏めていく. まずはそのデータ構造について主にどんな操作が出来るか(それをアルゴリズムと言う)を書き, なんかこういうのに使ったね, こういうのと同じ形だね, みたいなのを思い出して書いていく.
グラフ
-
出来る操作
-
幅優先・深さ優先探索
-
最短経路導出
-
最小全域木導出
-
巡回セールスパーソンの経路導出
-
最大流(最小カット導出)
-
グラフ彩色
-
応用
-
古典的な画像処理の領域抽出(グラフカット)
-
ネットワーク工学の色々(最小全域木でルーティング, 最大流で伝達効率上げる, とか)
-
オペレーションズ・リサーチ(配送業者がどう荷物運ぶ?的な)
-
オートマトン
-
リカレントニューラルネットワーク
-
ボルツマンマシン
-
コンパイラがレジスタ割付けをする時にグラフ彩色を使うらしい
-
電気回路理論でグラフっぽい事習ったがあまり記憶にない…
DAG
-
出来る操作
-
トポロジカルソート
-
グラフに出来る事は大抵出来そう
-
応用
-
命令スケジューリング(コンピュータアーキテクチャでパイプライン化とかする時に)
-
プロセス実行の順番(OS)
-
畳み込みニューラルネットワーク
-
高速フーリエ変換のバタフライ演算
-
Gitもマージありならそうだなあ
-
DAG型ブロックチェーン(分岐だけでなく融合もする)ってあるらしい.
本気か -
タグによる整理はDAG型か. タグが親
-
関係データベース管理システムはDAGっぽい気がするけど(カラムとレコードという2つの親を指定すると子が決まる)良く分からん
-
感想
-
タスク管理的なのとか高度なデータベース管理っぽいのが多いなあ(グラフを管理できるデータベースも盛んに研究されてるっぽいけど)
木
-
出来る操作
-
ソート出来る(と言うかソートを速くする為に木を使う場合が多い)
-
探索出来る(同様)
-
応用
-
データベース(Bなんちゃら木をよく聞く. とはいえグラフやDAGへの拡張が研究されている)
-
WebのDOM構造
-
メジャーなブロックチェーン
-
プログラミング言語(構文木)
-
自然言語処理
-
文字列処理
-
ディレクトリ構造
-
文脈自由文法で生成される文
-
ゲーム木ってのもあるなあ(DAGにもなるのでは思ったりもする)
-
感想
-
言語っぽいのが多い
ヒープ
-
出来る操作
-
操作というか, ヒープソートの実装に使える
-
優先度付きキューの実装に使える
-
応用
-
ヒープ領域とはあまり関係ない(実装によっては関係ある)
-
ハフマン符号の効率化に二分ヒープ使った気がするなあ
-
優先度付きキューはOSがタスク管理する時に重要っぽい
-
感想
-
ここから下は即応用というより他のアルゴリズムの下ごしらえのデータ構造みたいなのがちらほら出てくるなあ
連結リスト
-
出来る操作
-
挿入・削除・検索の速度とかメモリ使用量みたいなのを配列と比較されたりする
-
応用
-
エディタ実装する時は1行をノードとした二重連結リストの形で保存しましょうみたいなのあった気がするけど今のメジャーなエディタもそうやってんのかなあ
-
チューリングマシンに使うテープはあれ一応連結リストだろうなあ
スタック
- 応用
- 深さ優先探索に必要
- プッシュダウンオートマトンはメモリがスタックになっている
キュー
- 応用
- 幅優先探索に必要
わからんもの
- 計算論では(正規文法<文脈自由文法<チューリングマシン)順に強くなっていくみたいな事やりますね
- 文脈自由文法の文は[木っぽく生成される] (https://ja.wikipedia.org/wiki/%E6%96%87%E8%84%88%E8%87%AA%E7%94%B1%E6%96%87%E6%B3%95#%E5%B0%8E%E5%87%BA%E3%81%A8%E6%A7%8B%E6%96%87%E6%9C%A8 "")みたいなのはやると思います
- じゃあ正規表現とチューリングマシンはなんなのか
- 正規文法はリストっぽいなあ(例えば右正規文法だと右にしか伸びていかない事から心で感じ取って下さい)
- チューリングマシンはなんだ?
- 制限なく生成されるって事はDAGなのか?(グラフでない理由:流石にループするって概念なくないか?)
- 文脈自由文法とチューリングマシンの間に文脈依存文法もあるが, これは文が長くなっていく生成規則は認めないから, 「絶対に収束するDAG」みたいな?)
余談
- 自然数の集合は無限に長い連結リスト
- ペアノの公理によってどんどん後者が生成される
- じゃあ実数はそんな風に生成出来る?
- 「自然数の集合のべき集合(部分集合を集めた集合)」と「実数の集合」は同じ濃度(1対1対応出来る)
- DAGである[ハッセ図] (https://ja.wikipedia.org/wiki/%E3%83%8F%E3%83%83%E3%82%BB%E5%9B%B3 "")を書けば部分集合の生成もグラフで表現出来るなあ(もちろん無限にデカい)
- チューリングマシンも離散も連続もグラフで作れた, eeicどころか世界とはグラフ(悟り)(ぐるぐる目)