流体シミュレーションにおいて流れ場を可視化する際にはベクトルや流線を用いることが多いと思います.
今回は,ベクトルや流線よりも直感的に流れ場を理解しやすい粒子追跡(Particle tracking)を用いて流れ場の可視化を行います.
2次元キャビティ流れ
今回は差分法を用いて,以下に示すNavier-Stokes方程式のベンチマーク問題として有名な2次元キャビティ流れを解きます.
$$\frac{\partial{u}}{\partial{t}}+u\frac{\partial{u}}{\partial{x}}+v\frac{\partial{u}}{\partial{y}}=-\frac{\partial{p}}{\partial{x}}+\frac{1}{Re}\left(\frac{\partial^2{u}}{\partial{x^2}}+\frac{\partial^2{u}}{\partial{y^2}}\right)$$
$$\frac{\partial{v}}{\partial{t}}+u\frac{\partial{v}}{\partial{x}}+v\frac{\partial{v}}{\partial{y}}=-\frac{\partial{p}}{\partial{y}}+\frac{1}{Re}\left(\frac{\partial^2{v}}{\partial{x^2}}+\frac{\partial^2{v}}{\partial{y^2}}\right)$$
SIMPLER法として知られている圧力・流速の分離解法によってNavier-Stokes方程式を解きます.
SIMPLER法のアルゴリズムは以下の流れです.
今回は中心差分法を用います.
- Navier-Stokes方程式の圧力項を無視して仮の流速$\tilde{u}$と$\tilde{v}$を求める.
$$\frac{\partial{u^n}}{\partial{t}}+u\frac{\partial{u^n}}{\partial{x}}+v\frac{\partial{u^n}}{\partial{y}}=
\frac{1}{Re}\left(\frac{\partial^2{u^n}}{\partial{x^2}}+\frac{\partial^2{u^n}}{\partial{y^2}}\right)$$
$$\frac{\partial{v^n}}{\partial{t}}+u\frac{\partial{v^n}}{\partial{x}}+v\frac{\partial{v^n}}{\partial{y}}=\frac{1}{Re}\left(\frac{\partial^2{v^n}}{\partial{x^2}}+\frac{\partial^2{v^n}}{\partial{y^2}}\right)$$
$$\iff$$
$$\frac{\tilde{u}-u^n}{\Delta{t}}+u^n\frac{u^n_{j+1}-u^n_{j-1}}{2dx}+v^n\frac{u^n_{i+1}-u^n_{i-1}}{2dy}=\frac{1}{Re}\left(\frac{u^n_{j+1}+u^n_{j-1}-2u_j^n}{dx^2}+\frac{u^n_{i+1}+u^n_{i-1}-2u_i^n}{dy^2}\right)$$
$$\frac{\tilde{v}-v^n}{\Delta{t}}+u^n\frac{v^n_{j+1}-v^n_{j-1}}{2dx}+v^n\frac{v^n_{i+1}-v^n_{i-1}}{2dy}=\frac{1}{Re}\left(\frac{v^n_{j+1}+v^n_{j-1}-2v_j^n}{dx^2}+\frac{v^n_{i+1}+v^n_{i-1}-2v_i^n}{dy^2}\right)$$
ここで右肩の$n$は現在の時間ステップを表しています.
2. 仮の流速$\tilde{u}$,$\tilde{v}$を用いて以下に示す圧力のポアソン方程式を解くことで次に時間の圧力$p^{n+1}$を求める.
$$\frac{\partial^2{p^{n+1}}}{\partial{x^2}}+\frac{\partial^2{p^{n+1}}}{\partial{y^2}}=\frac{1}{\Delta{t}}\left(\frac{\partial{\tilde{u}}}{\partial{x}}+\frac{\partial{\tilde{u}}}{\partial{y}}\right)$$
$$\iff$$
$$\frac{p^n_{j+1}+p^n_{j-1}-2p^n_j}{dx^2}+\frac{p^n_{i+1}+p^n_{i-1}-2p^n_i}{dy^2}
=\frac{1}{\Delta{t}}\left(\frac{{\tilde u_{j+1}}-{\tilde u_{j-1}}}{2dx}+\frac{{\tilde u_{i+1}}-{\tilde u_{i-1}}}{2dy}\right)$$
3. 求めた圧力$p^{n+1}$を用いて以下の式により次の時間ステップの流速$u^{n+1}$,$v^{n+1}$を求める.
$$\frac{u^{n+1}-\tilde{u}}{\Delta{t}}=-\frac{\partial{p}}{\partial{x}}$$
$$\frac{v^{n+1}-\tilde{v}}{\Delta{t}}=-\frac{\partial{p}}{\partial{y}}$$
$$\iff$$
$$u^{n+1}=\tilde{u}-\frac{p_{j+1}^{n+1}+p_{j-1}^{n+1}}{2dx}\Delta{t}$$
$$v^{n+1}=\tilde{v}-\frac{p_{i+1}^{n+1}+p_{i-1}^{n+1}}{2dy}\Delta{t}$$
1に戻る.
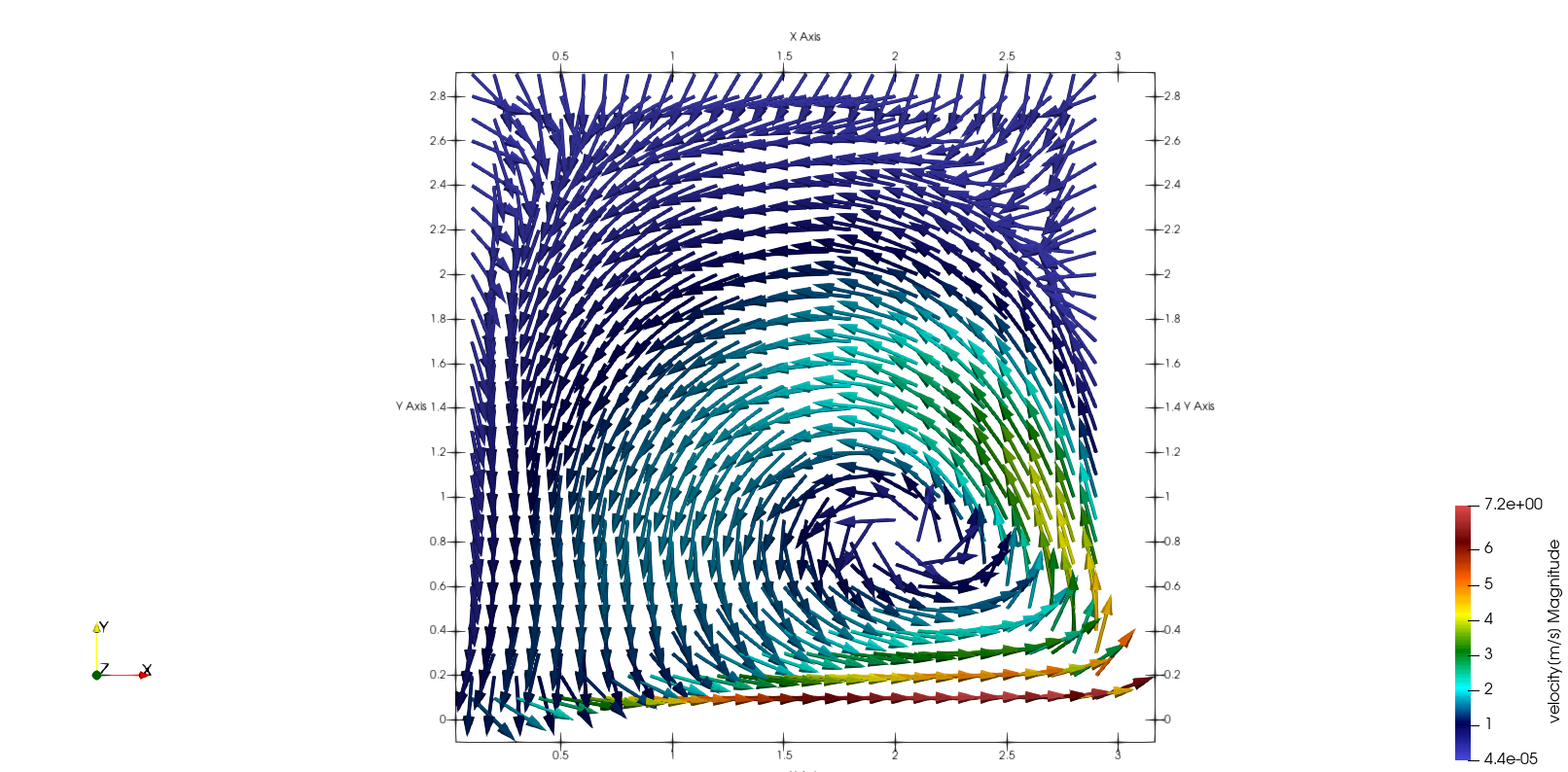
計算結果を以下に示します.今回は可視化としてParaviewを用いました.富岳のシミュレーションとかでも使われてるやつです.
計算条件は
時間刻み:$0.001$s
壁面速度:$10.0$m/s
空間解像度:$dx=0.1$m,$dy=0.1$m
計算時間10秒
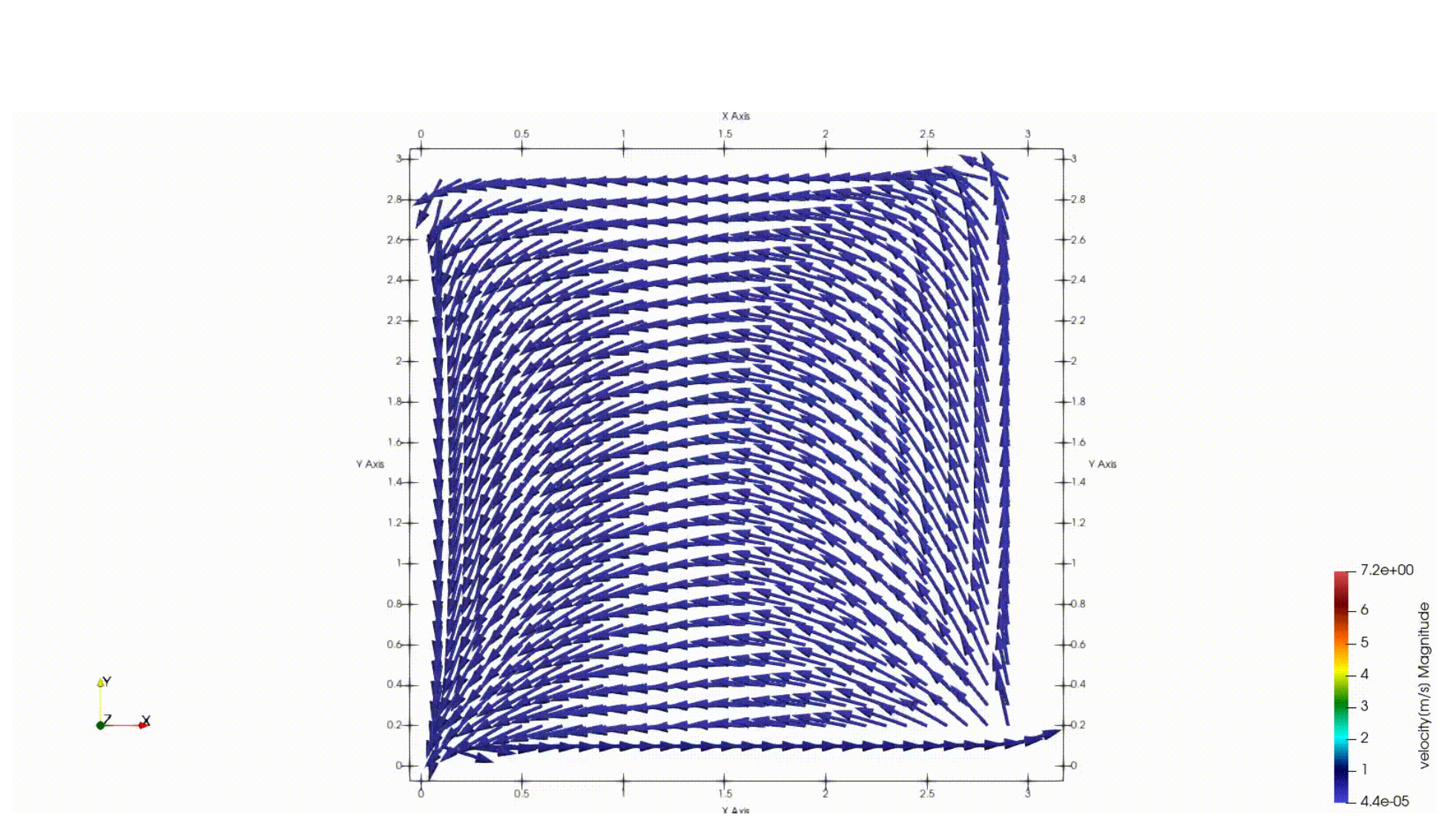
初期
粒子追跡による可視化
今回はとりあえず100000個の質量を考慮しない粒子を計算領域にばら撒きました.
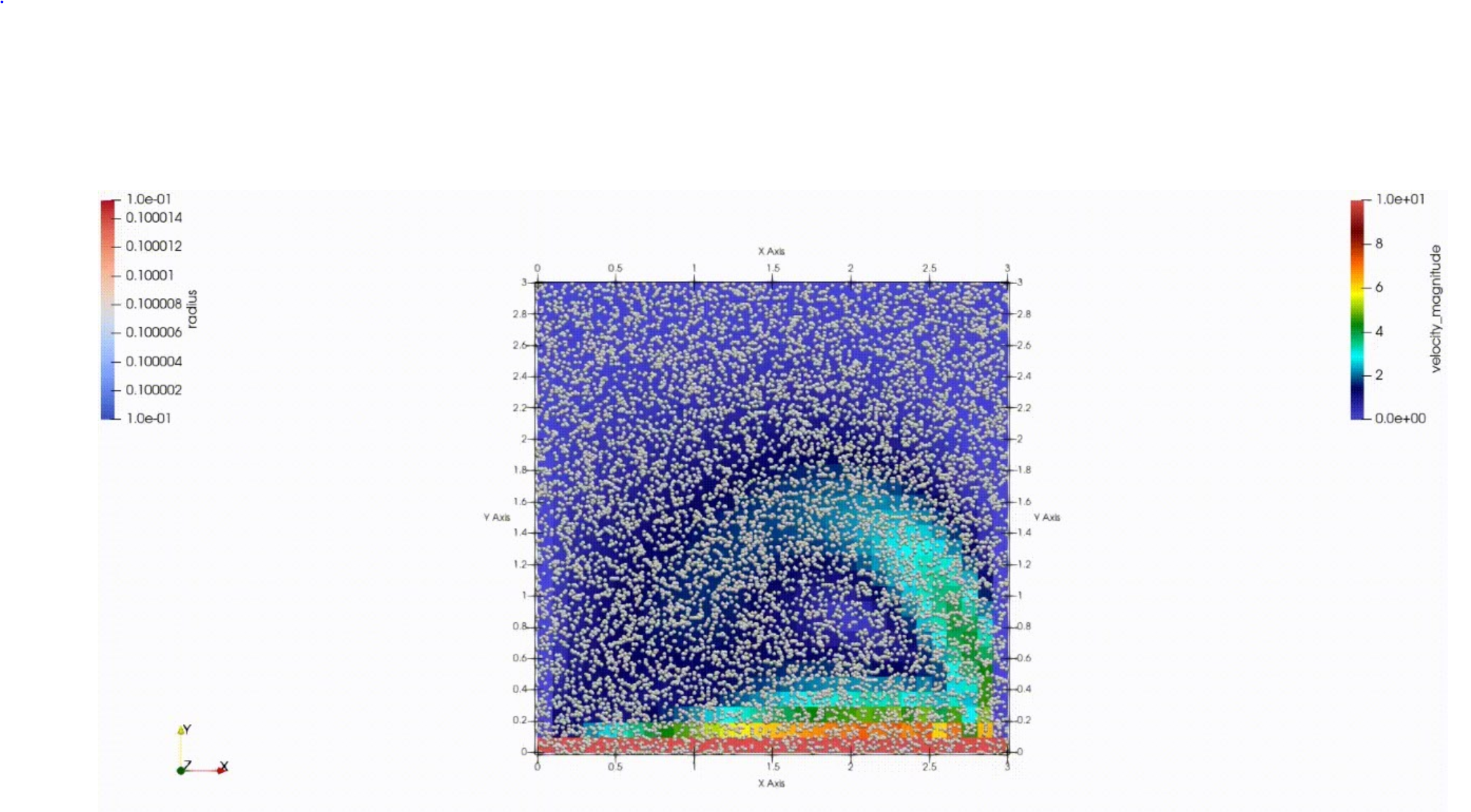
ここから各粒子について時間発展させ粒子の位置を更新していきます.
各粒子は以下の図に示すようにある格子状に存在します.
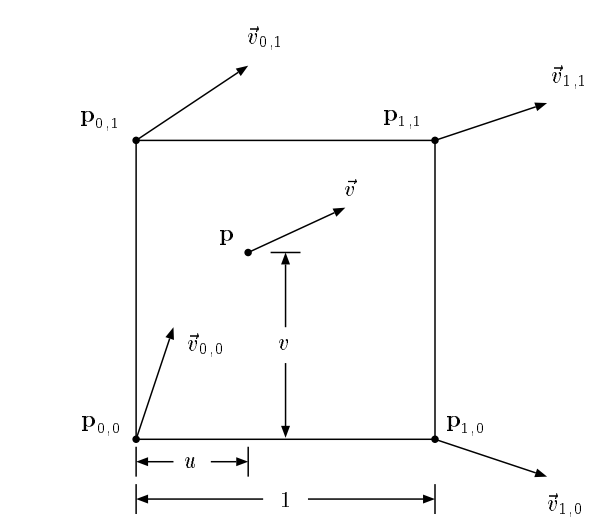
格子の四隅に定義された速度から粒子が持つ現時点での速度ベクトルを求めます.
上の図の場合だと以下の式で粒子速度ベクトルを求めることができます.
$$\vec{v}=(1-v)(1-u)\vec{v}_{(0,0)}+(1-v)u\vec{v}_{(1,0)}+v(1-u)\vec{v}_{(0,1)}+vu\vec{v}_{(1,1)}$$
最後に以下に示す4次のルンゲクッタ法で粒子の位置を更新します.
ここで$v$の下付き文字は時刻を表します.
$$\mathbf{p}_{i+1}=\mathbf{p}_{i}+\frac{1}{6}\Delta{t}\vec{v}_i+\frac{1}{3}\Delta{t}\vec{v}_{i+1}^1+\frac{1}{3}\Delta{t}\vec{v}_{i+1}^2+\frac{1}{6}\Delta{t}\vec{v}_{i+1}^3$$
ここで以下に示すように$\vec{v}_{i+1}^1$,$\vec{v}_{i+1}^2$,$\vec{v}_{i+1}^3$は粒子を少し動かして,動かした位置における次の時間ステップの流速を用いて求めます.
$$\vec{v}_{i+1}^1=\mathbf{p}_i+\frac{1}{2}\Delta{t}\vec{v}_i$$
$$\vec{v}_{i+1}^2=\mathbf{p}_i+\frac{1}{2}\Delta{t}\vec{v}_{i+1}^1$$
$$\vec{v}_{i+1}^3=\mathbf{p}_i+\frac{1}{2}\Delta{t}\vec{v}_{i+1}^2$$
ルンゲクッタの原理や意味についてはググってもらうと詳しい説明が出てくるかと思います.
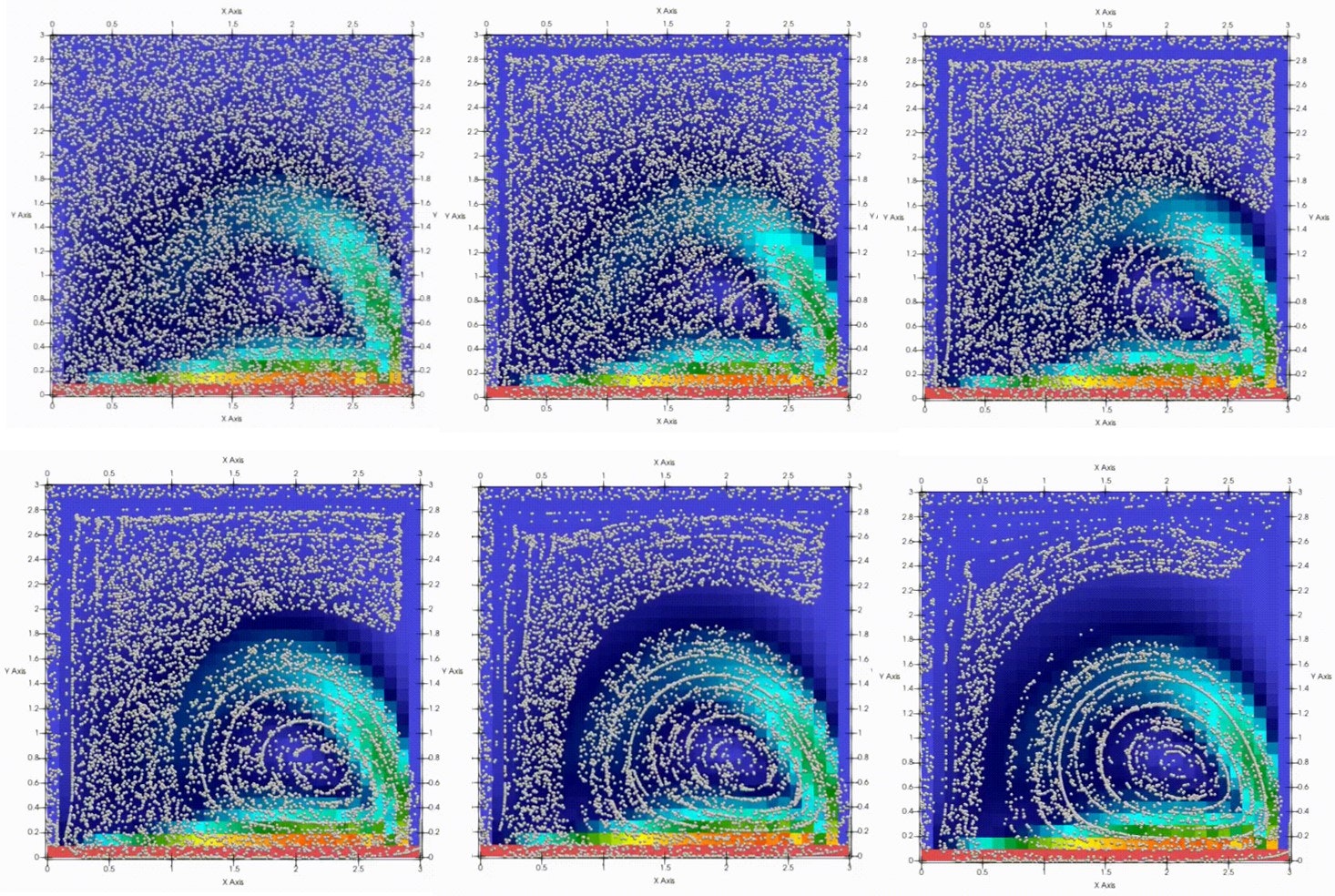
粒子追跡の様子をスナップショットで示しておきます.
本当は動画を貼りたいところですが...
参考文献
- 中山司,流れ解析のための有限要素法入門,東京大学出版会,2008
- Kenneth I. Joy, Numerical Methods for Particle Tracing in Vector Fields, Visualization On-Line Notes, 1999, February.
https://web.cs.ucdavis.edu/~ma/ECS177/papers/particle_tracing.pdf
最後に
最後に今回書いたコードのリンクを貼っておきます.
コードはC++で実装.
可視化はParaviewを,ポアソン方程式を解く際のSolverはEigenのQR分解を使っています.
https://github.com/syusaku625/particle_tracking
注意
今回は簡単化のためにレギュラー格子を用いています.
本当は圧力と速度の定義点を半格子分ずらしたスタガード格子を用いたほうが正確です.