そんなレイヤーがあったらいいなって、思ってね。
コードをgithubにあげました。
https://github.com/slowsingle/rotate_chainer
まずは以下の図をご覧ください。
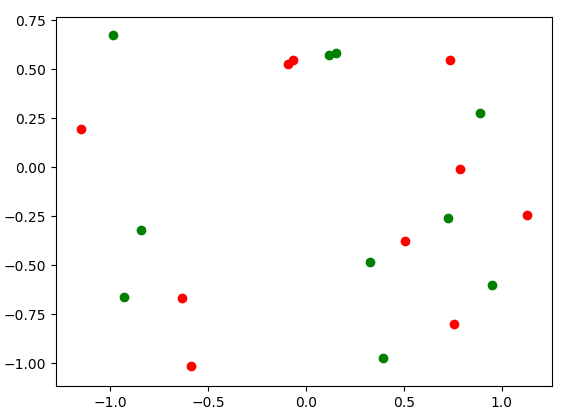
緑の点と赤い点が見えます。
この緑の点群に対してある回転行列を掛けて、ある並進ベクトルを足すと赤い点群と一致します。このときの$R$と$t$をDeep Learningのツールの1つであるChainerを使って解きたいと思います。
別にDeep Learningなど使わなくても解けたりしますが、まあ、たまにはレイヤーを使う立場から作る立場に立っても良いかな! と思ったのでね。それに点群が増えたときは簡単にGPU化できることがメリットになりますし。
ちなみに、こういう点群同士のマッチングはSFMとかSLAMとかでよく使われます。
定式化
Y = RX + t
上の図の緑の点群$X$(shape is (N, 2))、および赤い点群$Y$(shape is (N, 2))において、上の式を満たす$R$と$t$を求めれば良いのです。(Nは点群の数)
2次元の回転行列といえば角度$\theta$を用いて以下のように表されることはすでにご存知かと思います。
R =
\begin{pmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta
\end{pmatrix}
回転行列は2x2で、4要素ありますが、実質パラメータは1つです。つまり、回転行列には普通の2x2の行列(全結合層のパラメータ)ほどの自由度はないので、仮に全結合層をつなげて学習させた後の重み行列を引っ張ってきてもそれは回転行列から遠く離れた変換行列になっている可能性が高くなります。
では、次に勾配を求めたいと思います。chainerのbackward関数では以下の3つの行列およびベクトルを求めます。
\frac{\partial{Y}}{\partial{X}} \hspace{20pt}
\frac{\partial{Y}}{\partial{\theta}} \hspace{20pt}
\frac{\partial{Y}}{\partial{t}}
左からサイズは(2, 2), (N, 2), (1)です。
なお、計算すると以下のようになります。
\frac{\partial{Y}}{\partial{X}} = R \\
\frac{\partial{Y}}{\partial{\theta}} =
X{\frac{\partial{R}}{\partial{\theta}}}^T =
X{
\begin{pmatrix}
-sin\theta & -cos\theta \\
cos\theta & -sin\theta
\end{pmatrix}}^T
\\
\frac{\partial{Y}}{\partial{t}} = 1
backward関数には引数として、
\frac{\partial{L}}{\partial{Y}}
が与えられる(サイズは(N, 2))ので、
\frac{\partial{L}}{\partial{X}} = \frac{\partial{L}}{\partial{Y}}R^T \\
\frac{\partial{L}}{\partial{\theta}} =
sum(\frac{\partial{Y}}{\partial{\theta}} * \frac{\partial{L}}{\partial{Y}}) \\
\frac{\partial{L}}{\partial{t}} = sum(\frac{\partial{L}}{\partial{Y}}, axis=0)
が重みの更新として使われたり、入力層へ近いレイヤーへと伝搬していったりします。
$*$は要素積です。要素積を求めて、全部を足し合わせます。なので、サイズは(1)になります。
結果
あらかじめ回転角度および並進ベクトルを用意して、緑の点群に変換を行い、変換後の赤い点群を得ます。
次に、この2種類の点群から回転角度と並進ベクトルを推定し、緑の点群に変換を行い、青い点群を得ます。
赤い点群と青い点群が一致していれば推定成功というシナリオです。

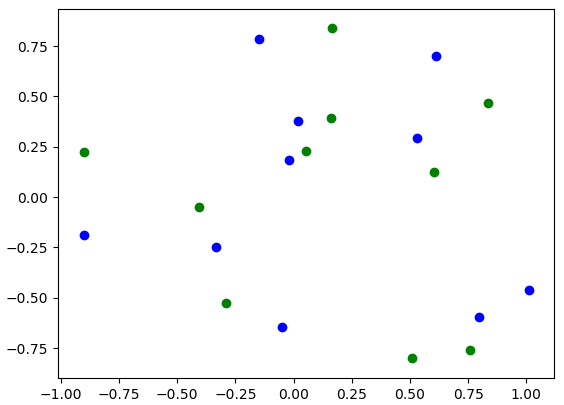
良い感じに推定が上手くいきました!
ちなみに、青い点群と赤い点群を同時にプロットすると点同士が重なって片方の色が覆い尽くされて見えなくなります。
なんだよ、このバグは…とちょっと悩んだりもしたのですが、推定成功してたからなんですね。良かったよかった。
上手くいかない点群もある
角度は$0=2\pi$ですよね。それが悲劇を生むのでした。
点群($X$や$Y$を指す)の座標値が大きいと、
\frac{\partial{L}}{\partial{Y}}
の値が大きくなって、$\pi$を超える勾配が生まれることがあります。普通の重みであれば特に大きな問題にはならないのですが、たとえば勾配として$2\pi$という値が与えられ、学習率1.0で修正すると、角度空間上では何の更新もされていないことになります。$0=2\pi$ですからね。
場合によっては、修正したい方向と真逆の方向に角度の舵を取られてしまい、わけのわからない値に更新してしまうことがあります。
なので、基本的には$X$および$Y$は-1~1の範囲に収まるよう正規化するのがベストでしょう。
もちろん、レイヤーの中でそういう問題が起きないように正規化処理を加えるのも手です。これはFuture Workとしましょう。
TODO
- 上記の正規化処理
- forward, backward関数のGPU化
- 3次元の回転にも対応させたい
- スケールも推定できるようにしたい(縦横比の違う点群同士のマッチングができる)
- 何か面白い使い道ないかなー