データ量が少ない場合はSVMを使ったほうがいい場合も多い。
サポートベクタマシンとはなんなのか
教師ありの機械学習手法で、実は分類だけでなく、回帰問題にも利用することができる。
とはいえ、多くの場合は分類問題に使うけれど。
n次元空間にプロットされたデータを扱います。
この、n次元ってのがイメージしづらいのですが、特徴量と考えるとわかりやすいかと。
超平面を使ってクラス分類することにしましょう。
超平面は、英語でHyper-Planeですね。
こんな感じで2値分類に、いい感じに使えます。
どうやって分類するの?
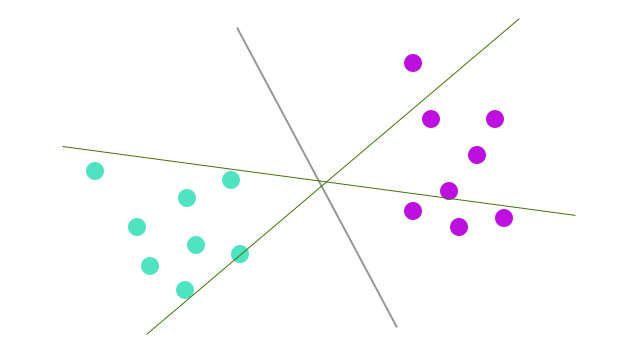
分類するときに、良い超平面はどうやって作るのか?という問題が出てきます。
超平面を追加してみました。
どれが一番良い超平面でしょうか?というと、明らかにもともとの線ですよね?
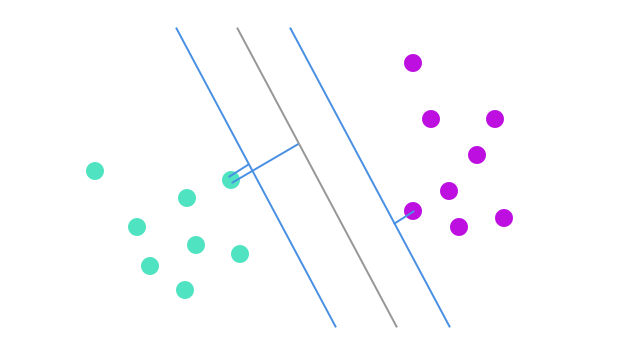
今度はどうでしょう?
各超平面から一番近い点(最近傍)との距離=マージンといいますが、これを使って良い平面を定義していきます。
真ん中の超平面が、マージンが最長です。マージンが長いほうが良い超平面であるとします。
マージンが長い=ロバスト性が高いといい、マージンが短い場合は誤分類の可能性がたかいと考えられます。
ここまで、直感的にわかると思います。
さて、次のケース。
青の線のほうがマージンは大きい。ですが、SVMではマージンの大きさよりも、正しい分類のほうが重要なので、ここでは、赤の線のほうがより良い超平面ということになります。
では、線形では分類できない問題の場合はどうでしょうか?
外れ値が混ざっています。
SVMは外れ値を無視して、マージンを最大化するような超平面を探します。SVMは外れ値に対してロバストです。
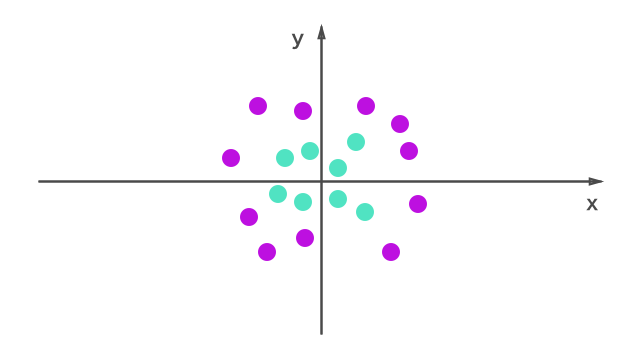
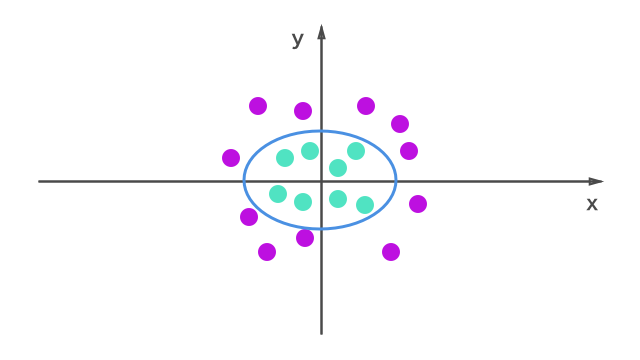
今度は、線形の分類はどう考えても無理な場合。
SVMの面白さは、このような問題を線形に分類できるところです。
$$z=x^2+y^2$$
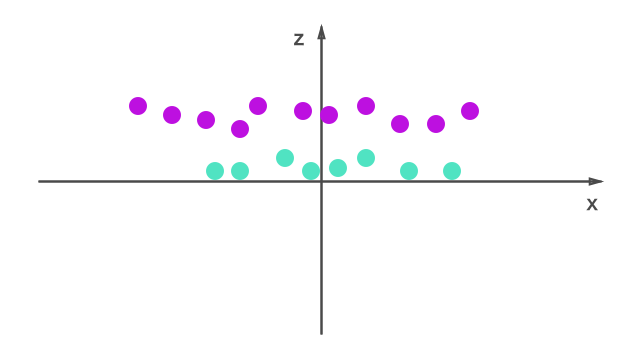
zという追加の特徴量をつくって、プロットし直してみます。
zの値は累乗のため常に正。
もともとのプロットで原点に近い点のz値は小さく、遠いものはz値も大きくなります。これによって、線形に超平面を引いて2値分類ができるようになります。
このzのように、都度特徴を追加していく必要があるのでしょうか。
SVMでは、カーネルトリックと呼ばれる技法を使うため、その必要がありません。
カーネルトリックは低次元のインプットを、高次元空間にプロットし直すことができます。非線形の分類問題に便利です。
元のインプットに対する超平面は、楕円のようなかたちになります。