最近いろんな種類の測定データに触れる機会が増えてきて「バックグラウンドの評価を試料や測定手法に依存せずにちゃちゃっと一括処理でやりたいな…」という気持ちが高まってきました。いろいろと探してみたところ、「ちょっと工夫するだけでピークを避けるような範囲指定をしないでもうまいことバックグラウンドのフィッティングができるよ」という論文をみつけました。ちょうどピークが動くせいで範囲指定が厄介な連続測定データがあったので「範囲指定いらないの最高じゃん」と思い早速採用して効果を実感したのですが、「もしかしたらバックグラウンド評価の技術って進歩してるのでは?」とふと思いもう少し深く掘ってみたところBEADSというアルゴリズムを発見しました。(ハイパーパラメータはあるけど)モデルフリーかつ高速にバックグラウンドを評価できるとのこと。試してみたらほんとにできちゃって「これはもっと広く知られるべきでは…」と思ったので紹介します。
背景
(早く実例を見たい方は準備から読んでも大丈夫です)
私が知っていたバックグラウンド除去
天文、物理、化学、生物などのあらゆる実験や測定で日々扱われているデータには必ずと言っていいほどバックグラウンド(分野によってはベースライン)と呼ばれる、できることなら測定にかからないでほしかったシグナルが含まれています。バックグラウンドが測定データに紛れ込む姿には様々な形があり、例えば、測定データ全体を一定の値や右肩上がり/下がりの直線で嵩上げするとても素直なものや複数の緩やかな丘が重なっているように見えるものがあります。
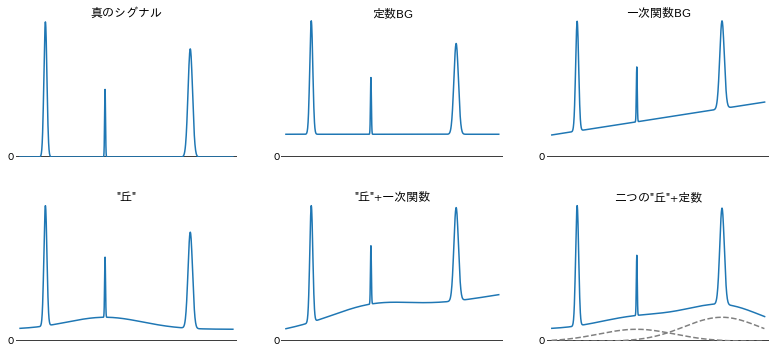
どんな実験データでも解析の第一歩はこういったバックグラウンドの評価ですが、実際に使われている評価方法は実験手法、試料の形状や構成元素、測定条件などによって異なります。一番ラッキーなのは、バックグラウンドの原因が分かっていて理論的に計算できる場合やバックグラウンドだけのデータを測定できる場合です。次にラッキーなのは測定機器メーカの提供するソフトウェアに自動バックグラウンド除去機能が含まれていて、ボタン一つでバックグラウンド除去済みのデータがポンッと出てくる場合でしょう。ラッキーではないほとんどの人たちがおそらく一番多く採用しているのは、うまいことバックグラウンドの形状を表現できそうな関数(多項式など)を使って最小二乗法などでフィッティングする方法だと思います1。このとき必要となる手順は以下のような感じでしょう。
- 測定データを眺める
- バックグラウンドを表現できそうな関数を定義する(例えば多項式なら何次まで使うか、など)
- フィッティングの対象にする「真のシグナルが含まれなさそうなバックグラウンドだけの測定点」を選ぶ
- 試行錯誤していい感じの初期値をみつける
- なんらかの出来合いのソフトウェアやパッケージをつかってフィッティングする
実は3の「フィッティングに使う測定点の選択」は冒頭で紹介した論文のコスト関数を正負で非対称にする方法を使うとスキップできるのですが、この話はここではしません2。そして3があってもなくても4はやはり面倒です。特に大量のデータを一括処理したいときに不都合が生じることがあります。
また、関数の定義にも不安があります。例えば上の図の右下にある「二つの"丘"+定数」の例では破線で示した二つのブロードなガウス関数と定数を真のシグナルに足しています。しかし、青い線だけをみて「このバックグラウンドはブロードなガウス関数二つに定数の下駄を履かせると表現できるな」と判断できる人は少ないでしょう。こういうときのとりあえずの選択肢となる多項式でもそこそこうまく表現できるかもしれませんが、次数決めと初期値探しに苦労しそうですし、やはり連続測定などの一括処理では不安が残ります。
2000年ごろからバックグラウンド評価技術に変化が
私が経験してきた物性物理、材料科学分野ではバックグラウンド補正は特段のペインとは考えられておらず、私を含めおそらく関数によるフィッティングやポチポチと点を選んで補完する方法を採用してる人が多いと思います。しかし、ラマン分光・IF-IR・クロマトグラフィー・質量分析・NMRといった、バックグラウンドの形状がやっかいな測定を使うコミュニティではより良いバックグラウンド評価技術を探る動きが2000年ごろから活発になったようです3。それらの中でも特に有名になり以降のベンチマークに必ず登場するようになったairPLS(adaptive iteratively reweighted penalized least squares)というアルゴリズムの2010年発表の論文でそれまでに発表された主な手法がカテゴリ分けされています。曰く、だいたいの手法が
- 多項式フィッティング
- ペナルティまたは重み付き最小二乗法
- ウェーブレット変換(周波数空間での分離)
- 微分
- robust local regression
に分けられ、それぞれにそれなりの良し悪しがあります。本稿はバックグラウンド評価技術全般に言及するつもりはないので、ここでこれらの技術についてはこれ以上触れません。興味のある方はairPLSの引用をたどって調べてみてください。測定データによってはBEADSよりもよい性能が出るものがあるかもしれません。
BEADS
BEADS(Baseline Estimation And Denoising using Sparsity)は2014年にChemometrics and Intelligent Laboratory Systemsという雑誌で発表されました(著者のDuvalさんが公開しているプレプリントもあります)。著者陣は信号処理コミュニティの方々ですが、クロマトグラフのベースライン処理問題の解決策として提案されたアルゴリズムです。
あまり数式を読み解くのは得意ではないのですが、このアルゴリズムのポイントは
- シグナル自体とその微分がスパースであることを仮定
- 非対称なペナルティも適用可能
- 凸最適化の一つであり漸近性が保証されているMM(Majorizer-Minimization)アルゴリズムを採用
という点であると理解しています。数式をベースに理解したい方は原著論文を見てください。この先は実例によってその威力を示していきます。
準備
オリジナルのBEADSはMATLABで書かれていますが、Python翻訳版を見つけたので、それをもとに実行速度をMATLAB版と同等レベルに改善するなどしたバージョンを作りました。
https://github.com/skotaro/pybeads/
PyPiにも公開してあるのでpipを使ってパッケージとしてインストール可能です。
pip install pybeads
この記事ではpybeadsを含め以下のパッケージを使います。
import numpy as np
import matplotlib.pyplot as plt
import pybeads
この記事と同じことをしているJupyter notebookもあります。
https://github.com/skotaro/pybeads/blob/master/sample_data/pybeads_demo.ipynb
サンプルデータ
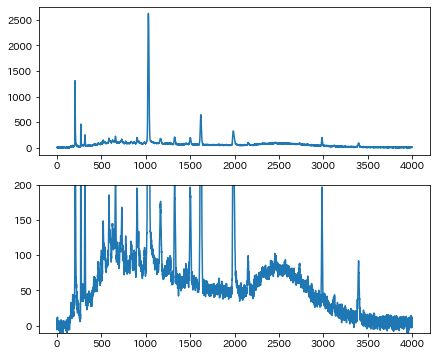
サンプルデータは https://github.com/skotaro/pybeads/blob/master/sample_data/chromatograms_and_noise.csv です。これはMATLABコードに添付されているクロマトグラフィーの実測定データdata/chromatograms.matと人工的なホワイトノイズdata/noise.matをMATLABフォーマットからCSVファイルに変換して一つのファイルにまとめたものです(再配布の許可は取得済み)。データ列は全部で9列あり、最初の8列はS/N比の異なる8つの実データ、最後の9列目はノイズ除去のデモンストレーションのために作ったと思われるホワイトノイズです。ここではバックグラウンドが特に大きい4番目のデータにノイズを加えたものを使ってみます4。
sample_data = np.genfromtxt('sample_data/chromatograms_and_noise.csv', delimiter=',')
y = sample_data[:, 3] + sample_data[:, 8]
print(y.shape)
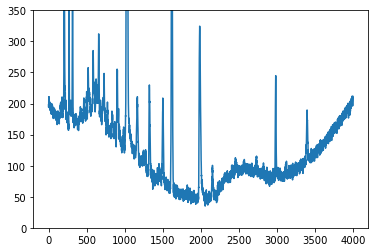
fig, axes = plt.subplots(2, 1, figsize=(7, 6))
axes[0].plot(y)
axes[1].plot(y)
axes[1].set_ylim(-10, 200)
クロマトグラフィーは詳しくないのでこのようなバックグラウンドがよくあるのかはわかりませんが、このバックグラウンドを多項式でフィッティングするとなると、初期値探しにちょっと苦労しそうです。早速このデータにBEADSを適用してバックグラウンドを推定してみます。
fc = 0.006 # ハイパスフィルター作成に使うcutoff周波数
d = 1 # ハイパスフィルター作成時のパラメータ。1でよい。詳細は論文参照。
r = 6 # 非対称ペナルティの非対称具合
# 測定データとその微分にかかる正規化パラメータ
amp = 0.8
lam0 = 0.5 * amp
lam1 = 5 * amp
lam2 = 4 * amp
# MMアルゴリズムのループ回数
Nit = 15
# ペナルティー関数
pen = 'L1_v2'
signal_est, bg_est, cost = pybeads.beads(y, d, fc, r, Nit, lam0, lam1, lam2, pen, conv=None)
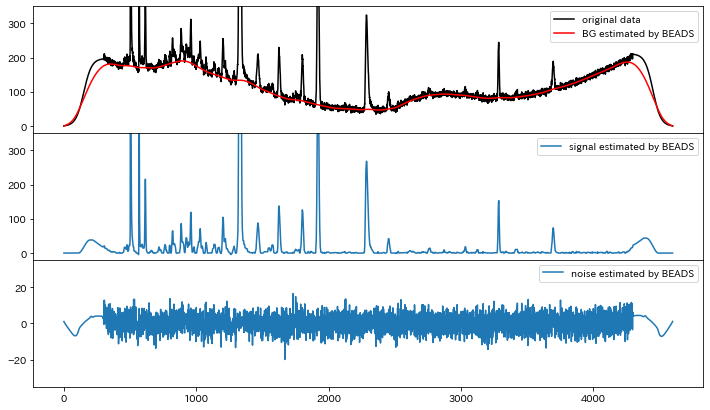
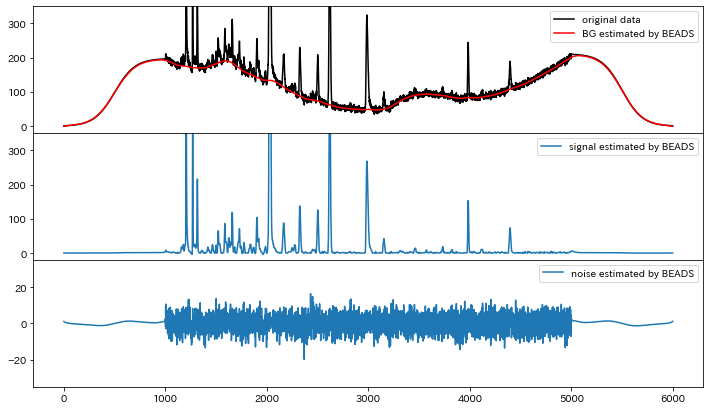
fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)
fig.subplots_adjust(hspace=0)
fig.patch.set_color('white')
axes[0].plot(y, c='k', label='original data')
axes[0].plot(bg_est, c='r', label='BG estimated by BEADS')
axes[0].legend()
axes[0].set_ylim(-20, 350)
axes[0].set_xlim(0, 4000)
axes[1].plot(signal_est, label='signal estimated by BEADS')
axes[1].legend()
axes[1].set_ylim(-20, 350)
axes[2].plot(y-signal_est-bg_est, label='noise estimated by BEADS')
axes[2].set_ylim(-35, 35)
axes[2].legend()
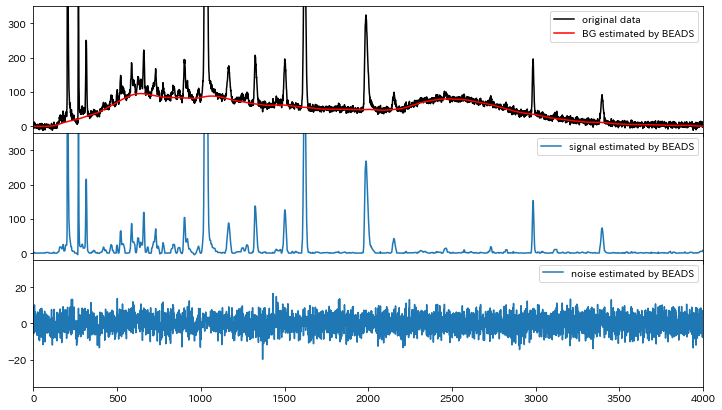
一番上のグラフの黒線がサンプルデータ。赤い線が推定結果です。驚きませんか?僕は「えっ…すごい…」って素直に驚きました。実行時間は4000点で400msくらいです。MATLABコードを使っている論文では1000点で120msなので、Python版でも速度は同等と言えそうです。また、ここまであまり触れてきませんでしたが、実は一番下のグラフにあるようにノイズの分離も同時にやっています。
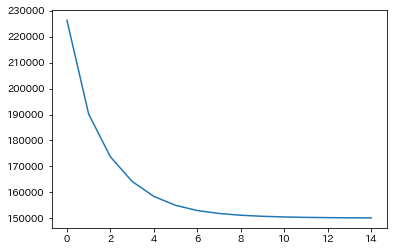
BEADSはループを回して解に漸近するMajorization-Minimizationアルゴリズムがベースなので、測定データと微分から算出したコスト(推定の良し悪しの目安)がループのたびにどう減ったかプロットすると設定したパラメータにおける解への収束具合が分かります。今回のデータは実行時に指定した15回で十分収束していると判断してよさそうです。
実データとの違い
実はこのサンプルデータは「データの両端で測定値が緩やかに0に落ちている」というBEADSにとって都合が良い性質を持っています。試しに定数を足して両端が0でないようにして、同じパラメータを使って推定してみます。
bg_const = 50
signal_est, bg_est, cost = pybeads.beads(y+bg_const, d, fc, r, Nit, lam0, lam1, lam2, pen, conv=None)
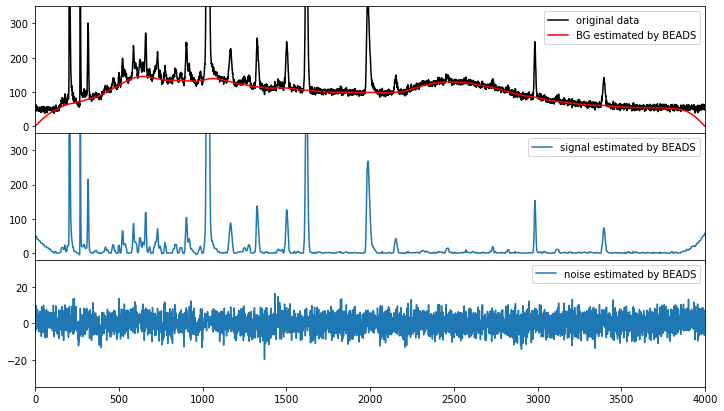
両端でうまく推定できていません。推定値が両端で0になっていることもわかります。
実際の測定データでは測定値が両端で滑らかに0になるとは限りません。これでは困ります。どうしましょう。
(0に)落ちぬなら落としてしまえ測定値
手元のデータで試してみてどうもうまくいかず「こんな素晴らしいアルゴリズムなのに両端で滑らかに0に落ちる測定データじゃないとダメなんて…」とがっくりきたのですが、上述のサンプルデータのトリックに気づき、滑らかに0になる部分を作って測定データを延長してしまえばいけるのでは?と閃きました5。
まず、どうせなら定数で底上げするよりももっとやらしい形のバックグラウンドにしてみます。
bg = 5e-5*(np.linspace(0, 3999, num=4000)-2000)**2
y_difficult = y + bg
plt.plot(y_difficult)
plt.ylim(0, 350)
大変やらしくなりました。これに延長部分をつけます。なめからに落ちていく関数にはシグモイド関数を採用しました。xscale_lなどはシグモイド関数の0に落ちる部分を"間延び"させるパラメータで、数字が大きいほど延長部分が"間延び"します。つまり0に落ちるまでに延長部分にたくさんの擬似測定点が足されます。ひとまず間延びパラメータは左右とも30にしてみます。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
xscale_l, xscale_r = 30, 30
dx = 1
y_difficult_l = y_difficult[0]*sigmoid(1/xscale_l*np.arange(-5*xscale_l, 5*xscale_l, dx))
y_difficult_r = y_difficult[-1]*sigmoid(-1/xscale_r*np.arange(-5*xscale_r, 5*xscale_r, dx))
y_difficult_ext = np.hstack([y_difficult_l, y_difficult, y_difficult_r])
len_l, len_o, len_r = len(y_difficult_l), len(y_difficult), len(y_difficult_r)
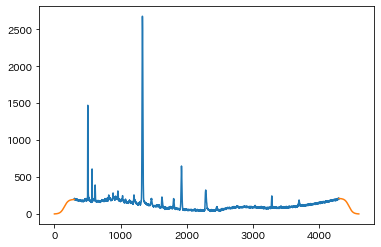
plt.plot(range(len_l, len_l+len_o), y_difficult)
plt.plot(y_difficult_l, 'C1')
plt.plot(range(len_l+len_o, len_l+len_o+len_r), y_difficult_r, 'C1')
オレンジの線が延長部分です。何となく良さそうに見えるので推定してみます。
signal_est, bg_est, cost = pybeads.beads(y_difficult_ext, d, fc, r, Nit, lam0, lam1, lam2, pen, conv=None)
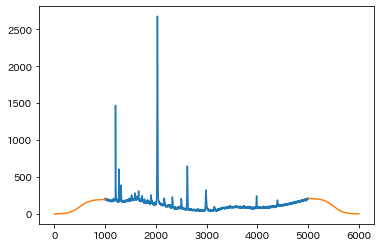
間延びがたりなさそうなものの、いい感じのアプローチにみえます。間延びパラメータを100にしてみます。
xscale_l, xscale_r = 100, 100
signal_est, bg_est, cost = pybeads.beads(y_difficult_ext, d, fc, r, Nit, lam0, lam1, lam2, pen, conv=None)
成功しました!これでおそらく(ピークがある程度スパースならば)どんな測定データでも対応できそうです。
ハイパラ調整について
さらっと流しましたが、BEADSはモデルフリーで関数を定義せずにバックグラウンドを推定できる一方で、ハイパーパラメーターがこれだけあります。
fc = 0.006 # ハイパスフィルター作成に使うcutoff周波数
d = 1 # ハイパスフィルター作成時のパラメータ。1でよい。詳細は論文参照。
r = 6 # 非対称ペナルティの非対称具合
# 測定データとその微分にかかる正規化パラメータ
amp = 0.8
lam0 = 0.5 * amp
lam1 = 5 * amp
lam2 = 4 * amp
# MMアルゴリズムのループ回数
Nit = 15
# ペナルティー関数
pen = 'L1_v2'
まだ数字の大きさの感覚には慣れていないのですが、少しいじった感じだとやはりどういう周波数以下のシグナルをバックグラウンドとするかを決めるfcが一番重要で、次に効くのが正規化パラメータです。実はデータによっては正規化パラメータを少し変えるだけ(例えば0.001から0.0011)で結果が大きく変わってしまうことがあります。その場合はconv=3かconv=5にしてみてください。微分結果が移動平均によりスムージングされ結果が安定します6。
d, r, Nit, penに関しては、データによるとは思いますが、私が扱うデータで変更する必要はありませんでした。
まとめ
- BEADSを使うと関数を定義せずにモデルフリーで測定データからバックグラウンドとノイズを推定・分離できる。
- 測定データによっては両端を滑らかに0にするような前処理が必要。
- ハイパラ調整は必要だが、実際に重要なパラメータは限られそう。
参考資料
- オリジナル論文(2014) https://doi.org/10.1016/j.chemolab.2014.09.014
- プレプリント laurent-duval.eu
- 論文著者によるプロジェクトサイト
- 元のMATLABコード
- MM algorithm - Wikipedia
-
他にもポチポチと選んだ点をスプライン補完や線形補完するという原始的ながら確実な方法があります。これは処理したいデータの数がそんなに多くない時やマニュアル操作によるブレがそんなに気にならないときには悪くない方法です。私は処理したい測定データが多いかつ手動でやる際のブレが気になるのと、なによりやってて悲しくなるのでこの方法は可能な限り避けます。ウェーブレット変換を使う方法もありますが詳しく調べる前に「もうBEADSでいいじゃん」となってしまい興味が薄れてしまいました。 ↩
-
バックグラウンド評価に適した関数がわかっていたり、関数による評価が必要な場合は非対称なコスト関数を使う方法はかなり有効で試す価値は十分あります。論文著者によるmatlabのツールボックスもありますが、
scipy.optimize.minimizeを使えばPythonでも簡単に書けます。 ↩ -
これらの測定手法は化学・生物・医学・食品といった産学共に研究者の多い分野で多用されているため、単純に需要が多く改善のインパクトが大きかったのも改善が進んだ一つの理由かなと思っています。 ↩
-
sample_dataの数値を見ると、ホワイトノイズを加える前から負の値が存在します。もしかしたら実データは生の測定データから両端を結ぶ線を引くような処理をすでにしてあるのかもしれません。 ↩ -
これはなにも測定データを捏造するというわけではありません。測定部分のバックグラウンドを推定するためだけに延長して、バックグラウンドを引いた後は延長部分を取り除けば何の問題もありません。 ↩
-
これは私がつけた機能なのでオリジナルのMATLAB版には(今のところ)ついていません。 ↩