タイトルを見て「何を当たり前のことを」という感想を抱かなかった人がこの記事を読むと少しは得るものがあるかもしれません。ただし、「は?なんのこと?」と思う人向けに書いたので「あーなるほど」という方には少し冗長な説明だと思います。
はじめに
国や分野が違うと同じものに由来の異なる名前がついているのはよくあることです。例えば日本語でフライドポテトと呼ばれる食べ物は、フランス語では「揚げ(frites)」、アメリカ英語では「フランス揚げ(French fries)」、ドイツ語では「(フランス語の)りんご(Pommes、フランス語のジャガイモ pomme de terre = "土のリンゴ"の省略形)」、中国語では「じゃがいもスティック(薯條)」と呼ばれています。それぞれの国や言語における文化的背景や料理の伝来ルートが反映されており面白いですね。棒状に切ったジャガイモを揚げた料理に言語ごとに色々な呼び名があるように、数学で畳み込み(convolution)と呼ばれる計算にも分野ごとに違う名前がついています。画像処理における平滑化(smoothing)やぼかし(blurring)1、統計や機械学習における密度推定(density estimation)がそうです2。つまり、それぞれの分野でカーネルや窓と呼ばれる重み付け係数に適切な規格化を施した同じ関数を使えば、どの操作も理論上は等価になります3。
この呼び方の違いは両分野の目的の違いをはっきりと反映してます。画像処理における畳み込みは、画像の見た目をきれいにする、二値化などの次の操作の邪魔になるノイズを除去する、被写体の特徴を抽出するといったことを目的にしています。オリジナル画像を目的に応じた"フィルター"に通して処理するという考え方から、こういった操作はまとめてフィルタリングとも呼ばれます。一方、統計では、誤差などの確率的な曖昧さを含む変数空間上の観測値を点ではなく「この辺にあるっぽい」として存在を滲ませることで散布図やヒストグラムから連続的で滑らかな分布を作り、限られた数の観測値から真の確率密度分布を推定することを目的にしています。この記事では、Pythonの画像処理ライブラリOpenCV、機械学習ライブラリScikit-learn、科学計算ライブラリScipyを使って、考えて見れば当たり前な、しかしなぜか(当たり前すぎて?)あまり指摘されることのないこの事実について述べます。
フィルタリングのカーネル、KDEのカーネル
どちらの分野でも、カーネル(kernel)や窓(window)と呼ばれる行列や関数が畳み込みに使われます。画像のフィルタリングの場合は、周辺ピクセルの重み付き和の計算につかう重み係数を定義した小さな行列をカーネルと呼び、フィルタリングの目的に応じて適切なものがだいたい決まっています4。以下のような図にすると画像フィルタリングにおけるカーネルが重み係数を並べた行列であることがよくわかります5。

密度推定におけるカーネルは、定義の上では、重み付き和に使う係数というよりは、下の図のように観測“点”の確率的な広がりを表現していると考えた方が良いです。
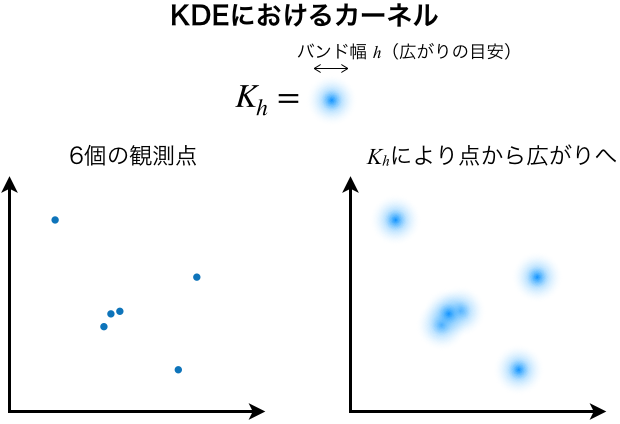
したがって、ピーク型の関数がカーネルとして使われており、特にどんなデータでも安定して妥当な結果を出してくれるガウス関数が重宝されています。この記事では、グレイスケール画像として捉えることもできる等間隔サンプリングした二次元ヒストグラムをガウシアンカーネルを使って平滑化・密度推定すると同じ結果が得られることを示します。
式から理解する
画像フィルタリングとKDEの演算が畳み込みであるということは、数式で同じように表現することができるということなので確認してみます6。
画像フィルタリングの定義は離散的な畳み込みそのもので表現されることが多いです。$f(x,y)$を入力画像、$\omega(x,y)$を$(2a+1)\times(2b+1)$ピクセル7のカーネル、$g(x,y)$を出力画像とすると、フィルタリングは以下のように書けます。
g(x,y)= (\omega *f)(x,y)=\sum_{s=-a}^a{\sum_{t=-b}^b{w(s,t)f(x-s,y-t)}}
数式で十分理解できる人には余計な話ですが、やっていることを画像処理の文脈で言葉を使って表現すると以下のように書けます。
フィルタリングされた出力画像のピクセル$(x,y)$の値は、入力画像のピクセル$(x,y)$とその周辺ピクセルの値にカーネルの係数をかけて求めた重み付き和である
一方で、KDEの定義は二変数の観測値であっても陽に畳み込みの形で表現されていません。カーネルの形状、つまり観測点を確率的な広がりとしてどれくらいぼんやりさせるかを決めるバンド幅を$h$としたとき、二変数の“真の”確率密度関数$f(x,y)$の推定$\widehat{f}_h(x,y)$は、カーネル関数$K_h(x, y)$を使ってよく以下のように書かれます。
\widehat{f}_h(x, y) = \frac{1}{n}\sum_{i=1}^n K_h (x-x_i, y-y_i)
$(x_1, y_1), (x_2, y_2) \dots (x_n, y_n) $は$n$個の観測点です。ここでは$(x, y)$の取れる値に特に制限は考えていないので離散的でも連続的でも構いません。右辺は観測点に原点を持つ(たいていピーク状の)カーネル関数を観測点の数だけ足しています。このKDEの定義を言葉で表現すると以下のようになります。
二変数空間上のある点$(x, y)$の確率密度の推定値は、$n$個の観測点をカーネル関数により滲ませた確率密度の点(x, y)における和である
このように言葉で表現すると、画像フィルタリングとKDEの定義がかなり似ていることがわかります。実は、KDEの定義式は、$n$個の観測点$(x_i, y_i),(i=1\cdots n)$を$n$個のデルタ関数$\delta(x)$で置き換えることで連続変数の畳み込みとしても表現できます。デルタ関数というのは、物理学者のディラックによって提案された、関数で点を表現する際に非常に都合の良い関数です。表記を簡略化するために二変数を$\mathbf{r}=(x,y)$と書き直すと、$n$個の観測点$\mathbf{r}_i,(i=1\cdots n)$のデータセットを表す関数$f_X(\mathbf{r})$は
f_X(\mathbf{r}) = \frac{1}{n}\sum_{i=1}^{n} \delta(\mathbf{r}-\mathbf{r}_i)
と表せ、$f_X(\mathbf{r})$をカーネル関数$K_h(\mathbf{r})$で畳み込みをすると、先ほどのKDEの定義が出てきます8。
\begin{eqnarray}
(f_X * K_h)(\mathbf{r}) &=& \int_{\mathbb{R}} f_X(\mathbf{r} - \mathbf{r}') K_h(\mathbf{r}') d\mathbf{r}' \\
&=& \int_{\mathbb{R}} \frac{1}{n}\sum_{i=1}^{n} \delta(\mathbf{r}-\mathbf{r}'-\mathbf{r}_i) K_h(\mathbf{r}') d\mathbf{r}' \\
&=& \frac{1}{n}\sum_{i=1}^{n}\int_{\mathbb{R}} \delta(\mathbf{r}-\mathbf{r}'-\mathbf{r}_i) K_h(\mathbf{r}') d\mathbf{r}' \\
&=& \frac{1}{n}\sum_{i=1}^{n} K_h(\mathbf{r}_i-\mathbf{r}) \\
&=& \frac{1}{n}\sum_{i=1}^{n} K_h(\mathbf{r}-\mathbf{r}_i)
\end{eqnarray}
最後の式変換はたいていのカーネル関数$K_h(\mathbf{r})$が原点に関して点対称$K_h(\mathbf{r})=K_h(-\mathbf{r})$であることを利用しています。
絵を描いて理解する
この話は二次元であるがゆえに、図を使っても正確さを失うことなく直観的に説明することができます。まずはフィルタリングとKDEの定義通りの演算を図示してみましょう。下の図は、位置Aにおけるフィルタリング・KDEの結果に位置BとCの値がどう寄与するかを表しています。
フィルタリングではカーネルの範囲に含まれないCは無視されていてます。KDEの定義通りの計算ではAから遠いCの寄与も(ほぼ無視できる程度ながら)考慮されています。図で使っているのはガウシアンカーネルと呼ばれるガウス関数を使ったカーネルです。フィルタリングでは5×5ピクセルのカーネルの例を描いています。KDEでは、ピクセル状の格子は引いてありますが、ひとまずヒストグラム化する前のデータ点を考えています。画像と同等に扱ってよい二次元ヒストグラムデータでも議論は全く変わりません。標準偏差が1ピクセルになるようなバンド幅を使ったガウシアンカーネルの場合は、積分すると全空間の積分値の99.999%程度になる$8\sigma+1=9$ピクセル四方の範囲だけを考える近似がよく使われます。
定義通りのKDEの演算を表す図と畳み込みとして解釈した時の図を並べてみます。
定義通りの場合は位置Aにおける推定値はBやCが滲んで薄まった値の和として表現されています。この滲み具合は各点からAまでの距離に依存するカーネル$K_h(\mathbf{r}-\mathbf{r}_i)$の値で決まりますが、等方的なカーネルの場合だとこの値はAを中心としたカーネル$K_h(\mathbf{r}-\mathbf{r}_A)$のBやCにおける値と等価です。つまり、Aにおける推定値へのBやCの寄与は、Aを中心としたカーネル関数$K_h(\mathbf{r}-\mathbf{r}_A)$のBやCでの値を重み係数に使った重み付き和を考えればよいことになります。これは、二次元ヒストグラムデータにガウシアンカーネルを使う場合は、一辺$8\sigma+1$ピクセルの正方形の領域のみを考えた畳み込みをすることと同じです。
ライブラリの準備
実際に計算してみます。インポートするライブラリは以下です。OpenCV、SciPy、scikit-learnの説明はいらないでしょう。Astropyは天文学分野で人気のオープンソースライブラリです。畳み込み関数にNaN(例:観測データの欠損や強すぎるシグナルなどによる測定無効領域)を補完する機能があるのがとても便利です。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# 二次元データ作成用
from numpy.random import multivariate_normal
from numpy.random import seed
# ガウシアンカーネル用
# 規格化済みのGaussian2DKernelもあるが、やっていることを明示的にするために規格化が必要なGaussian2Dを選択
from astropy.modeling.models import Gaussian2D
# 各種畳み込み+KRR
import cv2 as cv # バージョン3でもcv2なので注意
from astropy.convolution import convolve as astroconv
from scipy.ndimage import convolve as scipyconv
from scipy.stats import gaussian_kde as scipykde
from sklearn.neighbors import KernelDensity
# imshowの原点(0, 0)が左下にくるように初期設定を変更
plt.rcParams['image.origin'] = 'lower'
# 各ライブラリのバージョン
from astropy.version import version as astroversion
from scipy.version import full_version as scipyversion
from sklearn import __version__ as sklearnversion
print('scikit-learn:', sklearnversion)
print('scipy:', scipyversion)
print('openCV:', cv.__version__)
print('astropy:', astroversion)
# scikit-learn: 0.19.0
# scipy: 0.19.1
# openCV: 3.3.1
# astropy: 3.0.1
二次元データの用意
二峰性の二次元正規分布からサンプリングした擬似的な観測値を11000個用意します。
seed(1000) # 乱数の再現用シード
sig = 0.5 # 二次元正規分布の標準偏差
cen = [(4,6), (6,3)] # 二つピークのあるデータ
data = np.vstack([
multivariate_normal(cen[0], cov=[[sig**2, 0.5], [0.5, sig**2]],
size=10000), # 共分散行列の非対角項が非ゼロ=異方的なピーク
multivariate_normal(cen[1], cov=[[(sig)**2, 0], [0, (sig)**2]],
size=1000) # 対角項のみ=等方的なピーク
])
このデータを以下の三つの方法で可視化します。
- 11000個のデータを全て使って散布図として表示
- 11000個のデータ点をビン数50*50の二次元ヒストグラムとして表示
- ヒストグラムを画像として表示
nrow, ncol = 1, 3
subplot_kw = {'xlim':(1, 9), 'ylim':(1, 9), 'aspect':'equal'}
fig, axes = plt.subplots(nrow, ncol, figsize=(4*ncol, 3*nrow), subplot_kw=subplot_kw)
# 1. 生データのscatter plot
axes[0].scatter(data[:, 0], data[:, 1], marker='.', alpha=0.1)
axes[0].set_title('scatter(data)')
# 2. 生データのhist2d
xmin, xmax, ymin, ymax = 1, 9, 1, 9
nbin = 50
hist, xedg, yedg, img = axes[1].hist2d(data[:,0], data[:,1], bins=nbin,
range=[[xmin, xmax], [ymin, ymax]])
fig.colorbar(img, ax=axes[1])
axes[1].set_title('hist2d(data)')
# 3. ヒストグラムを画像として表示(imshow)
img = axes[2].imshow(hist.T, extent=[xmin, xmax, ymin, ymax])
axes[2].set_title('imshow(hist.T)')
fig.colorbar(img, ax=axes[2])
dataは(x, y)の座標が11000個並んだデータであり、histは50x50の各ビンの中にいくつデータ点があるか示すデータです。もちろん全ビンに含まれるデータ点の合計は11000個です。
print(data.shape)
print(hist.shape)
print(hist.sum())
# (11000, 2)
# (50, 50)
# 11000.0
後述しますが、この記事で扱う畳み込み関数が受け付けるデータ形式には、それぞれの関数が作られた目的に応じて、dataのような生の(x,y)座標データとhistのような等間隔ピクセルデータの二種類があります。ピクセル形式のヒストグラムは座標形式に"展開"する、つまりあるビン$i$に含まれる$n_i$個のデータ点をビンの座標$(x_i, y_i)$で観測されたとして$n_i$個のデータ点に復元することで、座標データしか受け付けない関数に渡すことが可能です。
ここで、のちほど規格化に使うヒストグラムのxとyの間隔を定義しておきます。
dx = (xedg[1:]-xedg[:-1]).mean()
dy = (yedg[1:]-yedg[:-1]).mean()
print(dx, dy)
print('eg.) x edge\n', xedg)
# 0.16 0.16
# eg.) x edge
# [ 1. 1.16 1.32 1.48 1.64 1.8 1.96 2.12 2.28 2.44 2.6 2.76
# 2.92 3.08 3.24 3.4 3.56 3.72 3.88 4.04 4.2 4.36 4.52 4.68
# 4.84 5. 5.16 5.32 5.48 5.64 5.8 5.96 6.12 6.28 6.44 6.6
# 6.76 6.92 7.08 7.24 7.4 7.56 7.72 7.88 8.04 8.2 8.36 8.52
# 8.68 8.84 9. ]
ヒストグラムデータと畳み込みの比較
SciPy, scikit-learn, OpenCV, Astropyを使った畳み込み及びKDEの結果と元のヒストグラムの差を確認してみます9。コードが多いので折りたたんでいます。詳細を見たい方は▶︎をクリックしてください。
データの用意
# KDE関数用にヒストグラムを"展開"した座標形式データを用意
X, Y = np.meshgrid((xedg + dx/2)[:-1], (yedg + dy/2)[:-1])
# ヒストグラムビンの位置=ピクセル位置
positions = np.vstack([X.ravel(), Y.ravel()])
hist_unpacked = []
x_temp, y_temp =[], []
for x, y, h in zip(X.ravel(), Y.ravel(), hist.T.ravel()):
x_temp.extend([x]*int(h))
y_temp.extend([y]*int(h))
hist_unpacked = np.vstack([x_temp, y_temp])
###### KDE (scipy) ######
# ヒストグラムを展開した座標形式データ
kde_hist = scipykde(hist_unpacked, bw_method=dx) # (ndim, npoints)
kde_scipy_hist = kde_hist(positions).T.reshape(X.shape)
kde_scipy_hist *= dx*dy*hist.sum() # 確率密度から元の値へ復元するスケール因子
# ヒストグラム化する前の生の座標形式データ
kde_raw = scipykde(data.T, bw_method=dx) # (ndim, npoints)
kde_scipy_raw = kde_raw(positions).T.reshape(X.shape) # Normalized density at the center of cells
kde_scipy_raw *= dx*dy*hist.sum()
###### KDE (scikit-learn) ######
kde_sklearn = KernelDensity(bandwidth=dx)
# ヒストグラムを展開した座標形式データ
kde_sklearn.fit(hist_unpacked.T) # sklearn: (n_samples, n_features)
kde_sklearn_hist = kde_sklearn.score_samples(positions.T).T.reshape(X.shape)
kde_sklearn_hist = dx*dy*hist.sum()*np.exp(kde_sklearn_hist)
# ヒストグラム化する前の生の座標形式データ
kde_sklearn.fit(data)
kde_sklearn_raw = kde_sklearn.score_samples(positions.T).T.reshape(X.shape)
kde_sklearn_raw = dx*dy*hist.sum()*np.exp(kde_sklearn_raw)
###### 畳み込みに使うカーネル(あるいは窓) ######
size = 15
X, Y = np.meshgrid(np.arange(size)-(size-1)/2, np.arange(size)-(size-1)/2)
g2d = Gaussian2D(x_stddev=1) # isotropic kernel
g2d.amplitude = 1/(2*np.pi*g2d.x_stddev*g2d.y_stddev)
window = g2d(X.ravel(), Y.ravel()).reshape(size, size)
###### Convolution, filter, blurring ######
conv_scipy = scipyconv(hist.T, window, mode='constant', cval=0)
conv_astropy = astroconv(hist.T, window)
filter_opencv = cv.filter2D(hist.T, kernel=window, ddepth=-1, borderType=0)
blur_opencv = cv.GaussianBlur(hist.T, ksize=(size, size), sigmaX=1, borderType=0)
非常に似通った二次元データの差をうまく可視化するために、diverging colormapの中心の白色部分が常に差分ゼロにくるように調整する関数を定義します。
差分をうまく表現するColorbarの定義
# https://stackoverflow.com/questions/7404116/defining-the-midpoint-of-a-colormap-in-matplotlibを一部改変
def shiftedColorMap(cmap, start=0, midpoint=0.5, stop=1.0, register=False, name='shiftedcmap'):
from matplotlib.colors import LinearSegmentedColormap
'''
Function to offset the "center" of a colormap. Useful for
data with a negative min and positive max and you want the
middle of the colormap's dynamic range to be at zero.
Input
-----
cmap : The matplotlib colormap to be altered
start : Offset from lowest point in the colormap's range.
Defaults to 0.0 (no lower offset). Should be between
0.0 and `midpoint`.
midpoint : The new center of the colormap. Defaults to
0.5 (no shift). Should be between 0.0 and 1.0. In
general, this should be 1 - vmax / (vmax + abs(vmin))
For example if your data range from -15.0 to +5.0 and
you want the center of the colormap at 0.0, `midpoint`
should be set to 1 - 5/(5 + 15)) or 0.75
stop : Offset from highest point in the colormap's range.
Defaults to 1.0 (no upper offset). Should be between
`midpoint` and 1.0.
'''
cdict = {
'red': [],
'green': [],
'blue': [],
'alpha': []
}
# regular index to compute the colors
reg_index = np.linspace(start, stop, 257)
# shifted index to match the data
if not midpoint in [0.0, 1.0]:
shift_index = np.hstack([
np.linspace(0.0, midpoint, 128, endpoint=False),
np.linspace(midpoint, 1.0, 129, endpoint=True)
])
for ri, si in zip(reg_index, shift_index):
r, g, b, a = cmap(ri)
cdict['red'].append((si, r, r))
cdict['green'].append((si, g, g))
cdict['blue'].append((si, b, b))
cdict['alpha'].append((si, a, a))
else:
shift_index = np.linspace(0.0, 1.0, 257, endpoint=True)
offset = 0.5 if midpoint == 0 else 0
for ri, si in zip(reg_index/2, shift_index):
r, g, b, a = cmap(ri + offset)
cdict['red'].append((si, r, r))
cdict['green'].append((si, g, g))
cdict['blue'].append((si, b, b))
cdict['alpha'].append((si, a, a))
newcmap = LinearSegmentedColormap(name, cdict)
if register:
plt.register_cmap(cmap=newcmap)
return newcmap
まずは各関数の結果と生のヒストグラムの差を確認します。
生ヒストグラムとの差分
data_list = ['hist.T',
'conv_scipy',
'filter_opencv',
'conv_astropy',
'blur_opencv',
'kde_sklearn_hist',
'kde_sklearn_raw',
'kde_scipy_hist',
'kde_scipy_raw',
]
nrow = 2
ncol = int(np.ceil(len(data_list)/nrow))
fig, axes = plt.subplots(nrow, ncol, figsize=(1.25*3*ncol, 3*nrow), sharex=True, sharey=True)
for ax, dat in zip(axes.ravel(), data_list):
if dat == 'hist.T':
diff = eval(dat)
cmap = plt.cm.viridis
else:
diff = np.around(hist.T-eval(dat), decimals=10)
midpoint = np.around((0-diff.min())/(diff.max()-diff.min()), decimals=3) # 1/256~0.004
cmap = shiftedColorMap(plt.cm.RdBu_r, midpoint=midpoint, name='shifted')
img = ax.imshow(diff, cmap=cmap)
cbar = fig.colorbar(img, ax=ax)
cbar.ax.tick_params(axis='y', direction='in')
ax.axis('off')
ax.set_title(dat, y=1)
fig.delaxes(axes.ravel()[-1])
どの関数の結果も元データに対してほとんど同じような差分を示しており、数式や図で確認した通り、画像のフィルタリングとKDEが少なくともほぼ同等の結果を示すことがわかります。
次に、各関数の結果の間にそれぞれどれくらいの差分があるか調べてみます。
各関数の差分
data_list = [#'hist.T',
'conv_scipy',
'filter_opencv',
'conv_astropy',
'blur_opencv',
'kde_sklearn_hist',
'kde_scipy_hist',
'kde_sklearn_raw',
'kde_scipy_raw',
]
nrow = len(data_list)
fig, axes = plt.subplots(nrow, nrow, figsize=(1.25*2*nrow, 2*nrow),
for i in range(len(data_list)):
for j, (ax, dat) in enumerate(zip(axes[i], data_list)):
ax.axis('off')
if i==0:
ax.set_title(dat, y=1.2)
if j==i:
ax.patch.set_visible(False)
continue
diff = np.around(eval(dat)-eval(data_list[i]), decimals=10)
midpoint = np.around((0-diff.min())/(diff.max()-diff.min()), decimals=3) # 1/256~0.004
shifted_cmap = shiftedColorMap(plt.cm.RdBu_r, midpoint=midpoint, name='shifted')
if np.nanmax(np.abs(diff)) < 1e-30:
ax.text(x=0.5, y=0.5, s='diff < 1e$\minus$30',
transform=ax.transAxes, ha='center', va='center')
continue
img = ax.imshow(diff, cmap=shifted_cmap)
cbar = fig.colorbar(img, ax=ax)
cbar.ax.tick_params(axis='y', direction='in')
cbar.ax.ticklabel_format(style='scientific', scilimits=(-2, 2))
差分の最大値が$10^{-30}$より小さいものは等価と見なして非表示にしました。カラーバーのオーダーを見ると$10^{-7}$や$10^{-10}$などというものもありますが、これは元データに対して0.0000001%以下です。原因はわかりませんが、実質的に同じと考えてもよいでしょう10。*_histと*_rawの差が大きいのは、ヒストグラム化前後の情報量の差です。また、SciPyのKDEだけ他の関数との差分が大きいのは、後述する通り、データから算出したバンド幅を使う仕様になっており、他の関数と共通の標準偏差を指定できなかったからです。残りは誤差の範囲で全て等価であると言えます。
同じ演算も名前で印象が変わる
同じカーネルを使ったフィルタリングと確率密度推定が等価な演算であることを知っていればなんてことないのですが、呼び方の違いは決定的な印象の差に繋がる可能性もあります。例えば、私が関わっている物質科学においては、両者が等価であると認識していない人が学会やグループミーティングで以下のようなセリフを聞くと、それぞれかなり違った印象を持ちそうです。
- 「ガウシアンを使い測定結果を畳み込みました」
- 「カウント数を確率密度とみなし、カーネル密度推定により真の強度分布を推定しました」
- 「データはガウシアンでスムージング(平滑化)しました」
1は数学的な記述で最も中立ですが中立すぎて目的がはっきりしません。2はKDEを知らない人にも正しそうなことをしてる印象を与えるでしょうが、KDEが統計学においてかなり広く使われ深く研究されている手法だという説明が必要かもしれません。一方、3はデータをスムーズにするという目的がはっきりしていている反面、聞く人によっては「ただ見た目を綺麗にするだけの余計かつよろしくないデータ操作なんじゃないか」という悪い印象を持つかもしれません11。表現を選ぶべきというと発表テクニックのような話にも聞こえますが、意図を簡潔に正しく伝えるのは重要です。もし、私がこのような説明の必要な場面に遭遇したら「統計学には観測データから真の値を推定するKDEと呼ばれる手法があるが、実は数学的にはただの畳み込みであり、画像処理分野ではスムージングと呼ばれる操作と等価である。この発表では(畳み込み|KDE|スムージング)と呼ぶ」といった説明をするでしょう12。
比較に使う各関数の注意点
以下は、各関数を定量的に比較するにあたって気をつけた部分です。記事の内容とは直接関係ありませんが、興味がある方もいるかもしれないので載せておきます。
scipy.ndimage.convolve
- 公式ドキュメント
- ピクセル形式データ(画像、二次元ヒストグラム)が対象。
- カーネルには任意の行列を指定可能な汎用性の高い関数。
- データの端での振る舞いは
mode=constant、cval=0としてデータの外側は0として扱うよう指定。
scipy.stats.gaussian_kde
- 公式ドキュメント
- 座標形式データが対象(生データかヒストグラムを"展開"したデータ)。
- 出力は確率密度なので元データと比較する際にはスケール因子が必要。
- 生データとヒストグラムの展開データを使った結果の間には、ヒストグラム化による情報の欠落に起因する差が生じる
- バンド幅は
bw_methodで指定した方法で必ずデータから決定される。つまり指定不可。bw_methodに値を指定した場合は、その値はデータの共分散行列のスケール因子として使われる。 - データの共分散行列に非対角項があれば、つまりデータが分布が異方的であれば、ガウシアンカーネルも異方的になる。他の関数では等方的な"丸い"ガウシアンカーネルを使っているため、特徴的な差分が生まれている。
cv2.filter2D
- 公式ドキュメント
- ピクセル形式データが対象。
- カーネルには任意の行列を指定可能。
- データの端での振る舞いは
mode=constant、cval=0としてデータの外側は0として扱うよう指定。 - データの端での振る舞いは
borderType=0としてデータの外側は0として扱うよう指定(ドキュメント) - 厳密には畳み込みではなく相関(correlation)を計算しているが、点対称なカーネルでは両演算は等価13。
cv2.GaussianBlur
- 公式ドキュメント
- ピクセル形式データが対象。
- カーネルはx方向とy方向の標準偏差を指定できるのみ。共分散行列は使えない。任意の行列を指定することもできない。
astropy.convolution.convolve
sklearn.neighbors.KernelDensity
- 公式ドキュメント
- 座標形式データが対象。
- 出力は対数確率密度なので元データと比較する際には指数関数$e^x$への代入とスケール因子が必要。
- ガウシアンカーネル(デフォルト)の場合、bandwidthは標準偏差。
- カーネルは等方的。
-
画像処理では、畳み込みではなく相互相関(cross correlation)で定義されている場合もありますが、カーネルが偶関数であれば両者は等価です。 ↩
-
画像処理を引き合いに出していることから分かる通り、二次元ヒストグラムで表現可能な二変数の観測データを念頭に置いています。 ↩
-
数学的には同じはずなのですが、実装の違いのせいか実際には無視できる程度のわずかな差が生じます。 ↩
-
フィルターの目的に対応したカーネルの形は英語版Wikipediaにまとまっています。 ↩
-
「数学的に等価である」と言わないのは、厳密さをあまり気にしない物理学科出身の私の説明にはきっと穴があるからです。 ↩
-
アルゴリズムの簡潔さや演算スピードの都合か、まず間違いなく正方形のものが使われます。また、カーネルの原点(中心)を元画像のピクセルとあわせるために各辺のピクセル数は奇数です。 ↩
-
r - "Kernel density estimation" is a convolution of what? - Cross Validatedの回答を一部改変。 ↩
-
本来なら座標形式データをとるKDE系関数と比べるべきなのは座標形式データですが、画像データを対象とする関数が多いので、KDEの結果もまとめてピクセル形式データであるヒストグラムと比べています。 ↩
-
おそらくアルゴリズムの差や丸め誤差の影響でしょう。 ↩
-
まさに私がそうでした。 ↩
-
()内は聴衆のタイプによって合わせるといいでしょう。個人的には、この説明を踏まえた上では何をやっているか想像しやすいスムージングがいいかなと思います。 ↩




