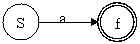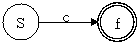むかし書いた有限オートマトン (FA; Finite Automaton) のメモ。
基本
- 決定性有限オートマトン (DFA; Deterministic Finite Automaton)
- 1 つの入力記号について、遷移先が一意に決定する。
- 非決定性有限オートマトン (NFA; Nondeterministic Finite Automaton)
- 1 つの入力記号について、遷移先が複数存在する。
- 入力なしで遷移できる $\epsilon$ 遷移が存在する。
DFA と NFA は相互に変換できる。
NFA の作り方
正規表現 (拡張バッカス記法) から作成する
正規文法 (バッカス記法) から作成する
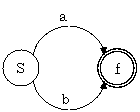
非終端記号は、規則の右辺の記号列に置き換わる(右辺の終端記号列を受理しようとしている)ので、これをオートマトンの状態とする。
正規文法では 1 つの還元動作が起こるとき、全ての入力受理が起こることになるので、どの非終端記号における終端記号の受理であっても最終状態 $f$ へ遷移する。
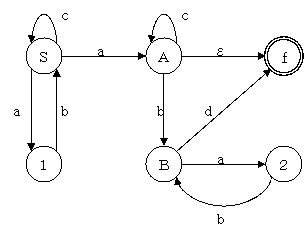
- $S \rightarrow a b S \mid c S \mid a A$
- $A \rightarrow c A \mid b B \mid \epsilon$
- $B \rightarrow a b B \mid d$
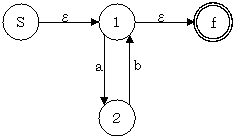
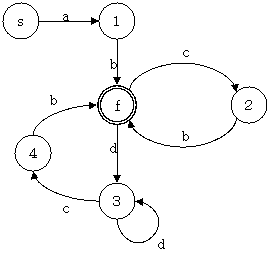
NFA から不用な ε を除去する
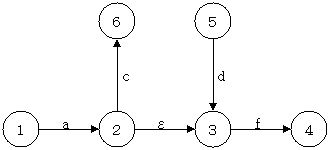
NFA には、存在しなくても受理できる記号列に影響を与えない $\epsilon$ が、存在している可能性がある。次の状態を満たさない $\epsilon$ 遷移は除去する.
- $\epsilon$ 遷移の遷移元から $\epsilon$ 以外による遷移が存在する
- $\epsilon$ 遷移の遷移先への他の状態からの遷移が存在する
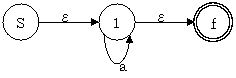
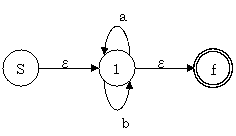
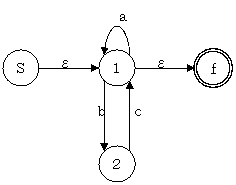
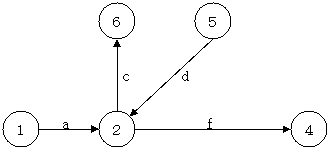
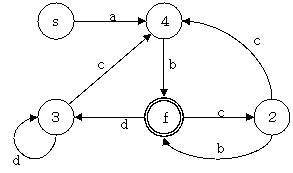
上の図で現在受理可能な記号列は、$ac$、$af$、$df$ の 3 つであり、$dc$ は受理できない。しかし 2 と 3 を一つにまとめてしまうと下図のように $dc$ が受理できてしまう.
NFA から DFA を作る
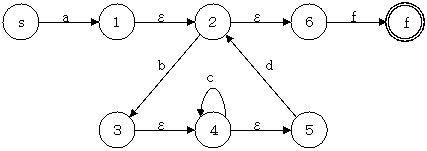
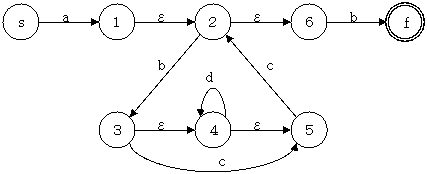
$a \{b (c \mid \{d\}) c \} b$
NFA の状態遷移表を作成
| 状態\入力 | $a$ | $b$ | $c$ | $d$ |
|---|---|---|---|---|
| $s$ | $1,2,6$ | - | - | - |
| $1$ | - | $3,4,5,f$ | - | - |
| $2$ | - | $3,4,5,f$ | - | - |
| $3$ | - | - | $2,5,6$ | $4,5$ |
| $4$ | - | - | $2,6$ | $4,5$ |
| $5$ | - | - | $2,6$ | - |
| $6$ | - | $f$ | - | - |
| $f$ | - | - | - | - |
$(1,2,6)$、$(3,4,5,f)$、$(2,5,6)$、$(4,5)$、$(2,6)$ を DFA の状態と考える。
NFA の状態遷移表から DFA の状態遷移表を作る
| 状態\入力 | $a$ | $b$ | $c$ | $d$ |
|---|---|---|---|---|
| $s,1,2,6$ | - | - | - | - |
| $1,2,6$ | - | $3,4,5,f$ | - | - |
| $3,4,5,f$ | - | - | $2,5,6$ | $4,5$ |
| $2,5,6$ | - | $3,4,5,f$ | $2,6$ | - |
| $4,5$ | - | - | $2,6$ | $4,5$ |
| $2,6$ | - | $3,4,5,f$ | - | - |
$(1,2,6)\rightarrow 1$、$(3,4,5,f)\rightarrow f$、$(2,5,6)\rightarrow 2$、$(4,5)\rightarrow 3$、$(2,6)\rightarrow 4$ と置き換える。
| 状態\入力 | $a$ | $b$ | $c$ | $d$ |
|---|---|---|---|---|
| $s$ | 1 | - | - | - |
| $1$ | - | $f$ | - | - |
| $f$ | - | - | $2$ | $3$ |
| $2$ | - | $f$ | $4$ | - |
| $3$ | - | - | $4$ | $3$ |
| $4$ | - | $f$ | - | - |
状態数を最小化する
同一化アルゴリズム
-
全ての状態を最終状態の集合とそうでないものの集合に分ける
-
各集合の要素である $s$ と $t$ に関して,次のように分割する
- $s$ または $t$ からある記号によって別の集合の要素へ遷移する場合
- ある記号による遷移が $s$ または $t$ のどちらか一方にだけ遷移する場合
-
これを繰り返して、どの集合も分割できなくなったら終わる。そのときの各集合を 1 つの状態とする
DFAが状態数最小のDFAである -
終状態の集合 $=\{f\}$ 分割の必要なし
-
それ以外の集合 $=\{1,2,3,4\}$
- $b$ で分割: $A=\{1,2,4\}$、$B=\{3\}$
- $c$ で分割: $C=\{1,4\}$、$D=\{2\}$
- $d$ では分割できない
-
よって、$\{1,4\}$、$\{2\}$、$\{3\}$、$\{f\}$ の 4 状態である