Numerical Recipes in Biomechanics #1 ~回転行列のキャリブレーション（平均化）~

Numerical Recipes in Biomechanicsについて

いかに問うべきか？

前職で，「動かして学ぶバイオメカニクス」や「モーションにおける３次元回転」のような記事を書いてきましたが，ここでは，そこで述べきれなかったこと，補足・訂正などを示していきたいと考えています．なお「モーションにおける３次元回転」はグループにすることを忘れていたようで，検索しにくかもしれません．お許しください．

また，「動かして学ぶバイオメカニクス」ではPythonコードも示しましたが，ここでは懐かしいNumerical Recipes in Cという有名な書籍のタイトルをオマージュし，記事を時々書いていきます．"Numerical Recipes in C"はとても良い本でしたが，Cでコードを書くことも減り，若い世代の方はご存じない方も多いでしょうが，数値計算の名著です．

いまやコードはChaGPTで変換すれば，Matlabでも何でも変換してくれますので，自分が使用する言語に変換することは可能でしょう．試しにここで取り上げた例をMathematicaのコードに変換することもできました．

問題の数理的な背景を理解していれば，AIにお願いすると大抵のコードを書くことができます．正しいとは限らないですが，問えばそれなりに答えてくれ，簡単な数学的な問題やアルゴリズムなら（多くの場合）適切に答えてくれます．それを頼りに勉強していけばアルゴリズムや数理的な理解も飛躍的に進みます．AIはプログラムもさることながら，（数学の凡人にはですが）数学的な理解を深めるには素晴らしいツールという印象です．未解決問題をAIに問うのは酷ですが，たとえばこの記事で考えている問題は，私が生まれたときに証明された問題で，その程度の数学問題にすぎず，誤りも少ないです．ネットで検索をすればきっとどこかに書いているでしょうが，圧倒的に答えにたどり着くのが早いという印象です（ただし，当たり前ですが問題に依存します）．

しかし，数理的な背景を理解していないと，そもそも質問が適切にできず，コードが正しいかどうかも判断できないでしょう．質問をするにしても最低限の数理的な理解が求められます．そもそも，どのようにAIに問えばよいのかという背景を言葉にする言葉が求められます．

ちなみに数学的な問題をAIに問うことや，バイオメカニクスの問題をAIにレビューすることは良いでしょうが，問う内容は誤らないでください．「なぜ短距離走者は腸腰筋が発達しているのでしょう？」などと問えば，レビューをしてくれるという意味では良いですが，バイオメカニクスでは理解が進んでいないことを示しています．つまり

「問い」を生成する思考回路の質が問われています．

するとここで書いていく記事もそれなりにまだ役立つと考え，「きっと探せばどこかには書いているが，それでもバイオメカニクスなどで必要なトピック」を「どのようにAIに問えば良いのか？」「背後にどのような数理的問題があるのか」ということを意識しながら，可能ならコード付きで今後示していくことを続けていきます．

はじめに

今回の話題に移ります．

計測データには必ず誤差が含まれます．たとえ変形しない剛体に貼付した２つの反射マーカを数フレームだけモーションキャプチャで計測し，その２点からベクトルを計算しとしても，それらが同じ方向を向き，同じ大きさとなる保証はありません．微小な変化が必ず発生します¹．

同様にモーションキャプチャで剛体にマーカを貼り付けて，その剛体の姿勢を正確な回転行列で表現することを念頭におき，静止している剛体を計測し，回転行列のキャリブレーションを行う方法をここでは考えます．

ベクトルの平均

図１：ベクトルの平均

計測対象が，たとえば２つのマーカの位置ベクトル（モーキャップで計測される座標）$\boldsymbol{x}_h, \boldsymbol{x}_0$から構成されるベクトルなら，通常行うことはベクトルの平均化です．全てのベクトルを加算し，計算に使用したベクトルの数で除すればよいわけです．もし，単位ベクトルを計算するなら，さらに，その平均化されたベクトルの大きさで除します．

たとえば，$\boldsymbol{k}$という同じ大きさと長さのはずのベクトルをモーションキャプチャで計測したとしましょう．そのベクトルの平均$\bar{\boldsymbol{k}}$は

$$
\bar{\boldsymbol{k}} = \frac{\sum_{i=1}^n \boldsymbol{k}_i}{n}
$$

と計算すればよいでしょう（図１）．ここで，$i$は時間と考えればよく，モーションキャプチャで$n$フレーム分計測を行ったとします．

これは一種のキャリブレーションです．

回転行列の平均

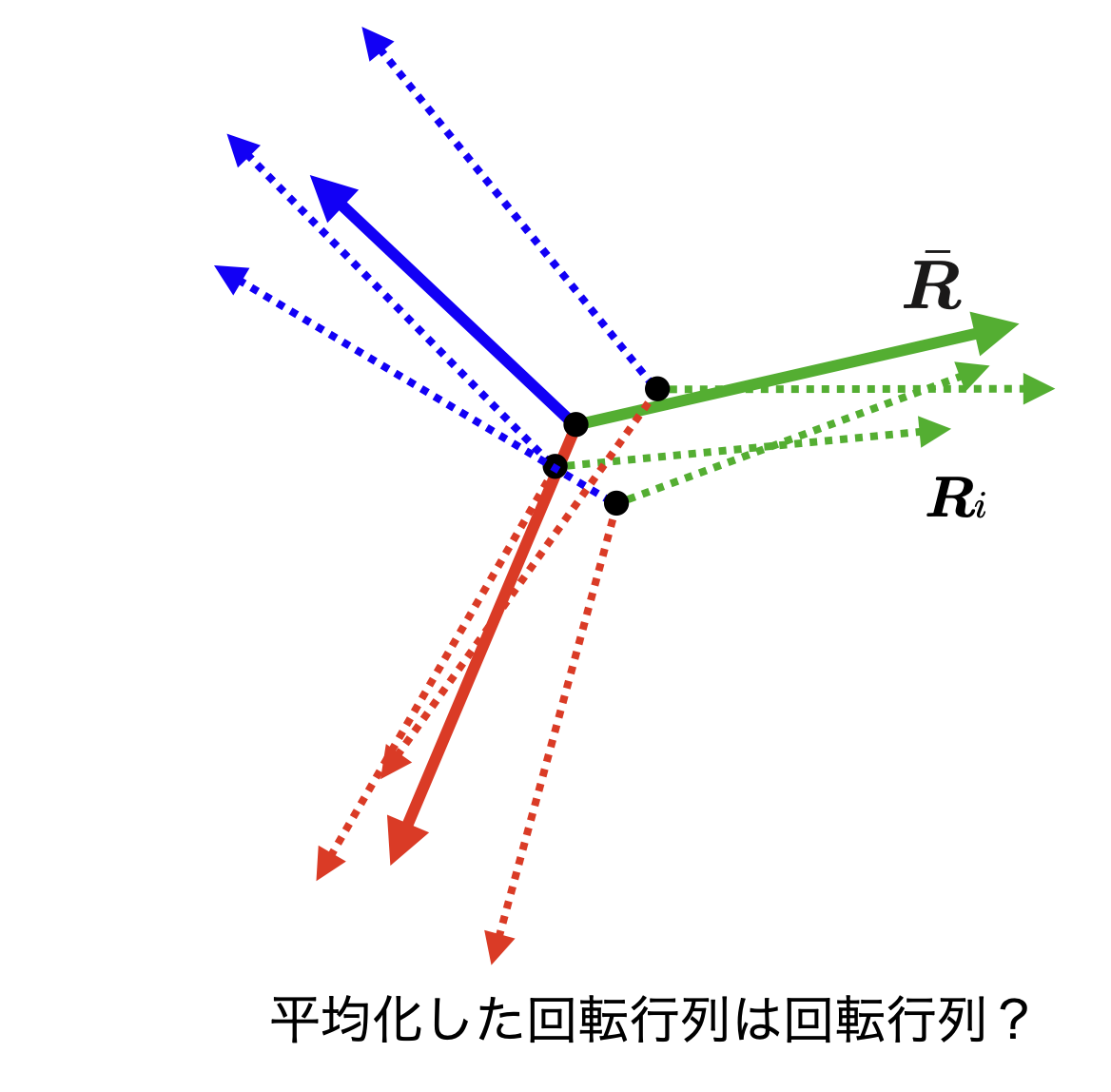
図２：回転行列の平均化？

では，静止した剛体に複数のマーカを貼付し，姿勢回転行列$\boldsymbol{R}_i$²を複数フレーム分，計算した後に，そのキャリブレーションはどのように行えばよいでしょう？

精度を気にしないなら，複数のデータではなくワンショットだけ計測するという手もありますが，精度を上げたいならやはり平均化する必要があるでしょう．通常ベクトルは２つのマーカの座標の引き算で計算できますが，剛体の姿勢は最低限３つのマーカが必要で，いくらか複雑な計算を行うことで姿勢回転行列を計算します．その複数の計算過程は，単にベクトルを計算する以上に誤差が発生するので，できるだけ精度を上げることが重要です³．

そこで，姿勢回転行列のキャリブレーションを

$$
\bar{\boldsymbol{R}} = \frac{\sum_{i=1}^n \boldsymbol{R}_i}{n}
$$

のように，単純に加算しその数で除すればよいでしょうか．答えはノーです．

ベクトルならその計算でよいのですが，回転行列は互いに直交する単位ベクトルを並べた直交行列という性質があります．平均化した回転行列が回転行列となるためには，この直交性を保つ必要があります．

そこで，「そもそも回転行列とは何か」，「行列における直交とな何か？」を簡単に述べます．

そもそも回転行列とは？

バイオメカニクスにおける３次元空間の回転行列の導入は，オイラー角，すなわち３つの座標軸による回転

$$
\begin{bmatrix}
\cos\alpha & -\sin\alpha & 0 \\
\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\cos\beta & 0 & \sin\beta \\
0 & 1 & 0 \\
-\sin\beta & 0 & \cos\beta
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\gamma & -\sin\gamma \\
0 & \sin\gamma & \cos\gamma
\end{bmatrix}
$$
という方も多いのではないでしょうか？ここでは，あまり深入りしませんが，回転をパラメータで表すことは，バイオメカニクスでは忘れたほうが良いです．回転は，この後，説明するように直交する単位ベクトルを並べて表現するほうが，精度，数理的な理解という意味でメリットが多いでしょう．

角度パラメータによる回転行列の表現は，回転の意味を直感的にはわかりやすい側面もあります，数理的な回転行列の理解をするためには，直交行列としての回転行列の意味を考えることも必要となりますので，まずはその直交性との関連について簡単にまとめます．

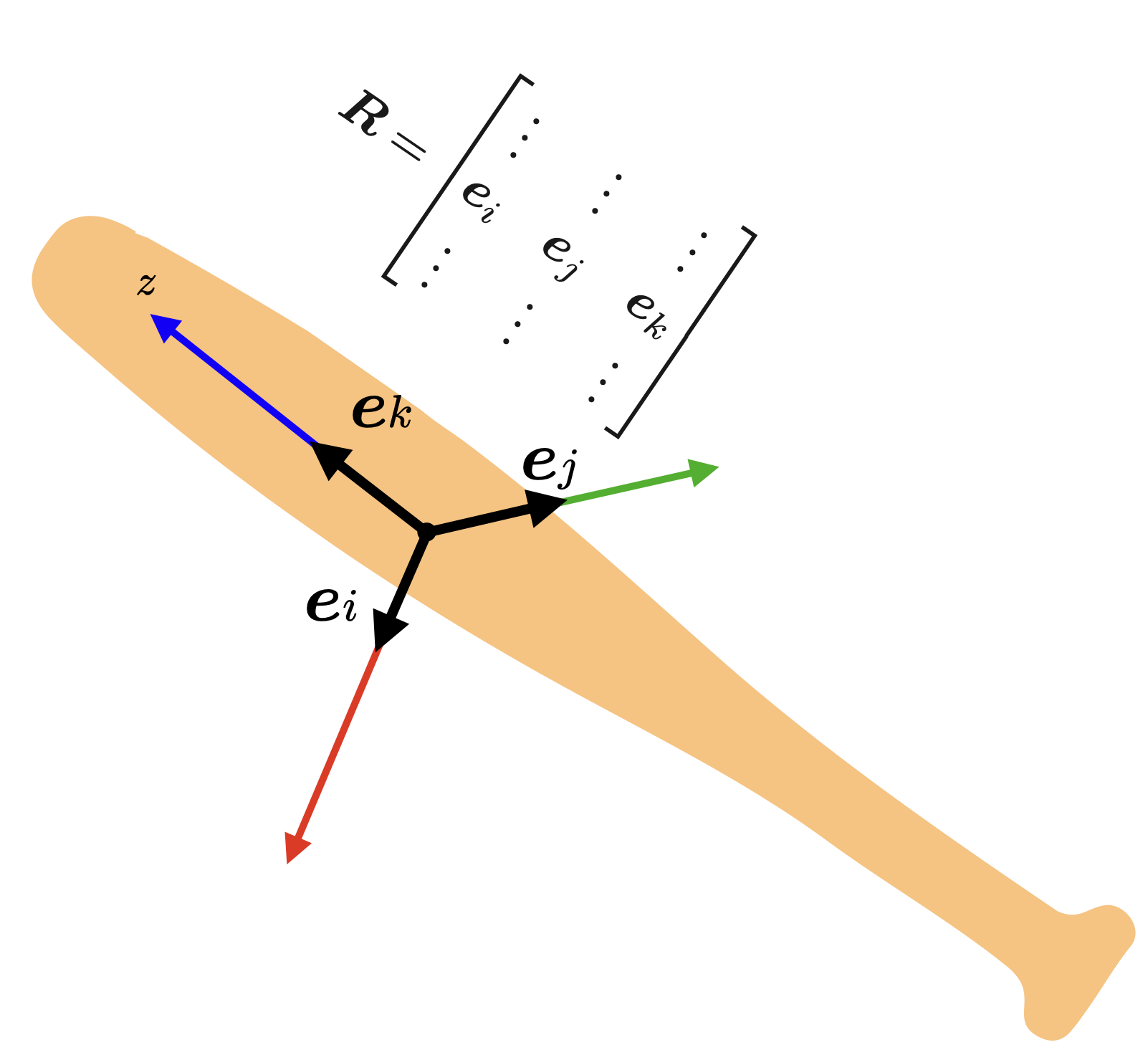
図３：正規直交基底

図３のようにバットに固定した座標系を考えます．これらの$xyz$座標軸に固定された単位ベクトルを$\boldsymbol{e}_i, \boldsymbol{e}_j, \boldsymbol{e}_z$を正規直交基底と呼びます．基底とは（３次元空間で）ベクトルを表現するために最低限必要な独立した要素のベクトルを意味します．正規は大きさ１，直交は各基底が直交していることを示しています．図３のようにバットに固定した座標系を考え，各$x$軸，$y$軸，$z$軸に，原点を始点とする単位ベクトル$\boldsymbol{e}_i, \boldsymbol{e}_j, \boldsymbol{e}_z$はりつけたものが正規直交基底です．この正規直交基底を並べた行列

$$
\boldsymbol{R} = \begin{bmatrix}
\vdots & \vdots & \vdots \\
\boldsymbol{e}_i & \boldsymbol{e}_j & \boldsymbol{e}_z \\
\vdots & \vdots & \vdots
\end{bmatrix}
$$

をこのバットの姿勢を表す姿勢回転行列として考えます．

この回転行列は

$$
\boldsymbol{R}^{-1} = \boldsymbol{R}^{T}
$$
のように転置行列が逆行列となる性質を持ち，これを直交行列と呼びます．ここで$\boldsymbol{R}^T$のように上付きで$T$の記号をつけた行列が転置行列です．

$$
\boldsymbol{A} = \begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{bmatrix}, \quad
\boldsymbol{A}^T = \begin{bmatrix}
a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
a_{13} & a_{23} & a_{33}
\end{bmatrix}
$$
のように対角成分（$a_{ii}$）はそのままで，非対角成分（$a_{ij}, i\ne j$）を入れ替えた行列が対角行列です．

このことは，回転の逆変換を計算する際，簡単に転置するだけですみます．回転行列の逆行列を計算するために通常の逆行列の計算を行ってはいけないことを示しています．同じ結果を得られるという意味で誤りではありませんが，明らかに無駄な計算です．

このような性質を持つことがわかれば，次のことも容易にわかります．

$$
\begin{aligned}
\boldsymbol{R}^T \boldsymbol{R} &= \begin{bmatrix} \boldsymbol{e}_x^T\ \\ \boldsymbol{e}_y^T \\ \boldsymbol{e}_z^T \end{bmatrix}
\begin{bmatrix}\boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z \end{bmatrix}
\\
&=\begin{bmatrix}
\boldsymbol{e}_x^T \boldsymbol{e}_x & \boldsymbol{e}_x^T \boldsymbol{e}_y & \boldsymbol{e}_x^T \boldsymbol{e}_z \\
\boldsymbol{e}_y^T \boldsymbol{e}_x & \boldsymbol{e}_y^T \boldsymbol{e}_y & \boldsymbol{e}_y^T \boldsymbol{e}_z \\
\boldsymbol{e}_z^T \boldsymbol{e}_x & \boldsymbol{e}_z^T \boldsymbol{e}_y & \boldsymbol{e}_z^T \boldsymbol{e}_z
\end{bmatrix}
\\
&= \begin{bmatrix} 1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix} = \boldsymbol{E}
\end{aligned}
$$

ここで$\boldsymbol{E}$は単位行列を表します．回転と逆回転を掛け算するともとに戻ることを示しています．

また，回転行列の転置と回転行列の積は，各基底ベクトル同士の内積（例えば，$\boldsymbol{e}_x^T \boldsymbol{e}_y$）で記述されていますが，直交する単位ベクトルの積は$0$ですから，非対角項が$0$となることを示しています．

つまり，図３の正規直交基底を順番に並べた回転行列$\boldsymbol{R}$は，直交行列（つまり$\boldsymbol{R}^T \boldsymbol{R} = \boldsymbol{E}$）の性質を満たします．

なお，行列$\boldsymbol{R}$が回転行列であるためには，さらに$|\boldsymbol{R}|>0$を満たす必要がありますが，これはまたどこかで述べることとしますが，鏡映（鏡で反転させる変換）を行う変換行列も直交行列となるためです．

先程も示しましたが，回転行列は

$$
\boldsymbol{R} = \begin{bmatrix}
\vdots & \vdots & \vdots \\
\boldsymbol{e}_i & \boldsymbol{e}_j & \boldsymbol{e}_k \\
\vdots & \vdots & \vdots
\end{bmatrix}
$$
のような構成（横に並べてもよい）になりますが，各基底ベクトルは

$$
\boldsymbol{e}_i^T \boldsymbol{e}_j = 0, i\ne j
$$
のように互いに直交し，

$$
|\boldsymbol{e}_i| = 1
$$

のように大きさが$1$となる性質を持っています．

過去の記事「動かして学ぶバイオメカニクス#10　〜角速度ベクトル〜」などにも記述していますのでご参照ください．

回転行列の平均化

複数の直交行列である回転行列を先に示した式のように平均化したときに，行列を構成するそれぞれの基底ベクトルの大きさが１で，互いに直交するという保証はありません．

そこで，平均化したあとに，平均化した行列を回転行列に修正する必要があります．

ここでは，特異値分解を用いた一般的な方法を述べます．この計算は最適化を行って導きます．証明は簡単ですが若干長いので，どのように計算を行うかだけを示します．

原理を知りたい方は，このあとに引用する文献や資料をご覧になってください．

特異値分解

特異値分解は，英語でSingular Value Decomposition (SVD)と呼びます．この分解は，数値計算ではいろいろなところで用いられます．固有値や主成分分析（PCA）と密接に関係します．シナジーの計算で使用する方もいます．今回のように正方行列でも，そうでない場合も計算できます．

特異値分解を理解したい方は，まずは，下記の特異値分解のWikiの図をご覧になるとよいでしょう．

Wikiより

行列の分解方法にはいくつもの方法がありますが，特異値分解は有用で最も強力に数値計算で使用される分解方法の一つです．

特異値分解は行列$\boldsymbol{M}$を

$$
\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^T
$$

のように特別な３つの行列$\boldsymbol{U}, \boldsymbol{\Sigma}, \boldsymbol{V}$に分解します．

このうち$\boldsymbol{U}, \boldsymbol{V}$は直交行列です．Wikiの図の$\boldsymbol{V}^{*}$と$\boldsymbol{U}$の回転に相当します．Wikiの${}^*$はここでの転置記号${}^T$に相当します．これは，回転行列と想像すればわかりやすいでしょう．

行列$\boldsymbol{\Sigma}$は

$$
\boldsymbol{\Sigma} =
\begin{bmatrix}
\sigma_1 & 0 & 0 & \cdots \\
0 & \sigma_1 & 0 & \cdots \\
0 & 0 & \sigma_3 & \cdots \\
\vdots & \vdots & \vdots & \ddots
\end{bmatrix}
$$
のような対角行列となります．$\sigma_i$は，特異値と呼び，各成分を伸縮する役割があります．固有値とほぼ同じ役割です．

つまりWikiの図と照らし合わせると，特異値分解は行列を３つの，回転$\boldsymbol{U}$→伸縮$\boldsymbol{\Sigma}$→回転$\boldsymbol{V}$を行う変換に分解します．Singular Spectrum Analysis (SSA) というフィルタリングも，時系列を行列に埋め込んで特異値分解（SVD）を行う方法です．あるシナジー解析では，この特異値（伸縮）を活用しますが，ここでは，平均化した行列を特異値分解し，直交行列である$\boldsymbol{U}, \boldsymbol{V}$を活用します．

つまり，平均化した回転行列$\bar{\boldsymbol{R}}$を

$$
\bar{\boldsymbol{R}} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^T
$$

のように特異値分解し，

$$
\hat{\boldsymbol{R}} = \boldsymbol{U} \boldsymbol{V}^T
$$

を計算すると，最適に回転行列として補正できます．

ここで述べる最適化とは，$\bar{\boldsymbol{R}}$は回転（直交）行列ではないので，「$\bar{\boldsymbol{R}}$に最も近い回転行列を最小化」になります．つまり，

$$
J = || \bar{\boldsymbol{R}} - \boldsymbol{R} ||^2_F
$$
を最小化する問題に置き換えると，プロクルステス問題（Procrustes problem）として知られている問題になります．ここで$||~||_F$はフロベニウスノルムを意味します．フロベニウスノルムが行列の「大きさ」を表すノルムの一つで，

　　　　　　　　　　　　　　

のように計算します⁴．

$\boldsymbol{U}, \boldsymbol{V}$は直交行列で，異なる直交行列の積も直交行列なので，$\hat{\boldsymbol{R}}$も直交行列となります．回転行列と置き換えて考えれば，回転行列の積も回転行列になることから，ここで証明は行わないですが，少なくともこれが回転行列になることは直感的に理解できるかと思います．

証明は現・名古屋工業大学の玉木先生の姿勢推定と回転行列をご覧になるとよいでしょう．長いですが，基本的な線形代数で容易に理解できます．

また特異値分解については書籍「線形代数の半歩先-データサイエンス・機械学習に挑む前の30話-」にとてもわかりやすく書いてあります．

Pythonコード

ChatGPTが書いてくれたコード（筆者が書いても，実質，同じコードになりますが，残念ながらあまり良いエンジニアではないので，ChatGPTのほうがきれいです）に少し手を加えて，示します．

ちなみに「複数の回転行列データの平均を計算するPythonコードを教えて下さい」とCurosrのエディタ内で，ChatGPTにコマンドKで質問をしただけです．

import numpy as np
def average_rotation_matrices(matrices):
    """
    複数の3x3回転行列の平均をSVDを使って計算する。
    引数:
        matrices: shape (N, 3, 3) のnumpy配列。N個の回転行列。
    戻り値:
        平均回転行列 (3x3 numpy配列)
    """
    assert matrices.ndim == 3 and matrices.shape[1:] == (3, 3), "各回転行列は 3x3 の形で与えてください。"

    # 行列の平均をとる
    M = np.mean(matrices, axis=0)

    # SVDを実行
    U, _, Vt = np.linalg.svd(M)

    # 平均回転行列
    R_avg = U @ Vt

    # 行列式が負なら反射行列なので修正
    if np.linalg.det(R_avg) < 0:
        U[:, -1] *= -1
        R_avg = U @ Vt

    return R_avg

このコードの最後のif文は，念の為，鏡映となることを防ぐためのコードです．よぽど，データが暴れていない限りは，鏡映とはならないでしょう．そこまで暴れるようではキャリブレーションが成り立つ状況とは言えません．

この程度であればChatGPTは完璧です．恐るべし．

参考コード

ChatGPTによる「モーションキャプチャ用の３つの反射マーカを剛体に貼付し，その位置座標からその剛体の姿勢回転行列を計算するPythonコード」

import numpy as np

def compute_rotation_from_three_markers(Q):
    """
    Q: shape (3, 3) → 各行がマーカーの世界座標（q1, q2, q3）
    戻り値: 3x3の回転行列 R
    """

    q1, q2, q3 = Q

    # x軸方向（q2 - q1）
    x_axis = q2 - q1
    x_axis /= np.linalg.norm(x_axis)

    # 仮想z軸（q2 - q1）と（q3 - q1）の外積（法線ベクトル）
    z_axis = np.cross(x_axis, q3 - q1)
    z_axis /= np.linalg.norm(z_axis)

    # y軸（z軸 × x軸）で右手系を作る
    y_axis = np.cross(z_axis, x_axis)
    y_axis /= np.linalg.norm(y_axis)

    # 回転行列を構築（列ベクトルとして）
    R = np.column_stack((x_axis, y_axis, z_axis))

    return R

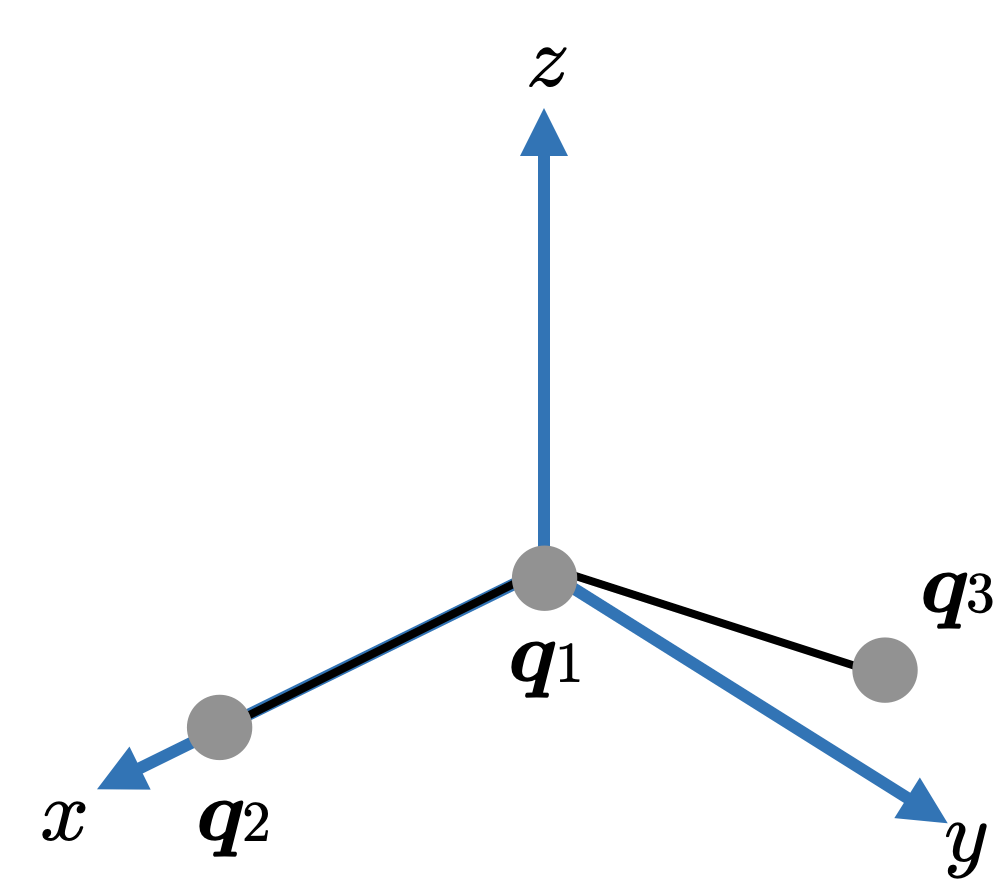
図５：マーカq1, q2, q3と座標軸の関係
「q1 を原点」「q2-q1 をx軸」「q1,q2,q3が構成する平面の法線をz軸」
　とするローカル座標系とみなした姿勢

1. モーションキャプチャの誤差を最も簡単に，かつ的確に精度を検証したければ，この「２つのマーカ間距離の変動」を調べるとよいでしょう．２点間距離は計測環境によって変化します．カメラと被写体が近ければ分解能が上がり変動は小さくなるでしょう．計測する場所を変えれば，それは変化しますし，たとえ同じ場所でも「２つのマーカの向きを変えるだけ」で精度が変わることもあります．複数のカメラで計測する以上，誤差の現れ方はとても複雑です． ↩

2. ChatGPTに「モーションキャプチャ用の３つの反射マーカを剛体に貼付し，その位置座標からその剛体の姿勢回転行列を計算する方法をPythonで教えて下さい．」と問うと，この脚注の上に示した参考コードを返してくれました．説明図を要求したところ正確でないので，筆者が作成しましました． ↩

3. 剛体に３つ，または４つなどの複数のマーカを貼付し，剛体の姿勢回転行列を定める方法はいずれNumerical Recipes in Biomechanicsという記事に書いていく予定です．それまでは過去に記述した動かして学ぶバイオメカニクス#9　〜身体各部の座標系〜などを参照ください． ↩

4. 行列の各成分の２乗和で，行列の全成分を一列に並べてベクトルとみなしたときのベクトルの長さの二乗（L2ノルム）と考えると良いでしょう． ↩