検査者の信頼性を評価する方法：級内相関係数について

はじめに

複数の評価者が同じ対象を評価した際の一致度や信頼性を測るための指標として、級内相関係数（Intraclass Correlation Coefficient：ICC）が利用されます。例えば、M-1グランプリの審査員が漫才グループのパフォーマンスを評価する場合、審査員間で評価がどれだけ一貫しているか、また評価の信頼性がどれだけ高いかを判別することができます。

本記事では、Rを用いたICCの分析例を紹介します。

利用するデータ

どうせならいつぞやのM-1グランプリの結果を題材にして分析しようと思ったのですが、思ったより露骨な結果が出たので、別のデータを使います。
今回はサンプルデータを生成してICCの分析方法を紹介します。
シチュエーションとしてはM-1グランプリを想定し、10組の漫才グループ(a~j)に対して、7人の審査員(A~G)が評価を行うというものです。
また、審査員の一人である審査員Bは、評価に偏りがあるものとします。

# ライブラリ読み込み
library(dplyr)
library(GGally)
library(purrr)

# ランダムシード設定
set.seed(42)

# 漫才グループ10組の真の点数を生成
true_score <- rnorm(n=10, mean=60, sd=10) |> round(digits = 0)

# 審査員ごとの評価にバラツつきを設定
adjustments <- rnorm(n=7, mean=0, sd=5) |> round(digits = 0)

# 真の点数をベースに、審査員ごとの点数を生成
score_data <- map_dfc(adjustments, ~ true_score + .x) |> 
  set_names(paste0("judge_", LETTERS[1:7])) |> 
  as.data.frame()
rownames(score_data) <- paste0("group_", letters[1:10])

# 各点数にランダムなノイズを追加し、さらに審査員Bに大きなノイズを追加
# 点数は整数にしておく
score_data <- score_data |> 
  mutate(across(everything(), ~. + rnorm(n(), mean=0, sd=5))) |> 
  mutate(judge_B =  judge_B + rnorm(n(), mean=0, sd=10)) |> 
  mutate(across(everything(), ~ round(., digits = 0)))

# 生成されたデータの表示
print(score_data)

生成されたデータは以下のようなマトリックスです。

        judge_A judge_B judge_C judge_D judge_E judge_F judge_G
group_a      68      74      63      80      73      82      75
group_b      49      77      35      51      38      62      49
group_c      78      80      57      66      64      71      58
group_d      71      93      60      67      63      64      73
group_e      62      74      55      59      64      67      64
group_f      65      82      56      66      61      65      58
group_g      88      97      64      77      81      73      73
group_h      75      61      45      58      54      59      52
group_i      85      74      75      80      86      86      82
group_j      65      55      48      61      60      66      57

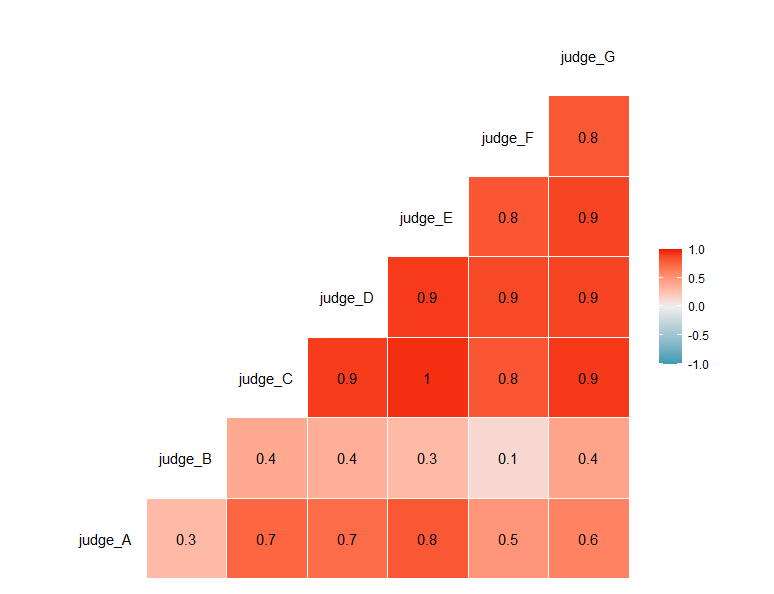
審査員間での相関も見ておきます。

# 審査員間の相関行列を計算して可視化
ggcorr(score_data, label = TRUE)

全体的に審査員同士で相関がありますが、審査員Bだけ相関が低いデータとなっています。

ICCの実施

ここからICCを使用して審査員の信頼性を評価していきます。
ICCには複数の種類がありますが、今回はICC(3)を使用します。似た手法としてICC(2)とICC(3)がありますが、それぞれの違いは評価の一般化の可否にあります。ICC(2)はランダムに選ばれた評価者の結果を、同じ特性を持つ他の評価者にも一般化するために使用されます。一方、ICC(3)は特定の評価者のみに焦点を当て、その評価者の信頼性を評価するために使用されます。

今回は、評価者の評価を一般化することに対して興味がなく、各審査員の評価の一貫性を測定することが目的であるため、ICC(3)を使用します。

※ ICCごとの利用ガイドラインや数理面について詳しく知りたい方はこちらの論文がお勧めです
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4913118/pdf/main.pdf

RではpsychライブラリのICC()で結果を得られます。

# ICCの結果確認
library(psych)
ICC(score_data)

Call: ICC(x = score_data)

Intraclass correlation coefficients 
                         type  ICC    F df1 df2       p lower bound upper bound
Single_raters_absolute   ICC1 0.48  7.5   9  60 2.7e-07        0.28        0.74
Single_random_raters     ICC2 0.50 13.9   9  54 3.2e-11        0.28        0.75
Single_fixed_raters      ICC3 0.65 13.9   9  54 3.2e-11        0.45        0.84
Average_raters_absolute ICC1k 0.87  7.5   9  60 2.7e-07        0.73        0.95
Average_random_raters   ICC2k 0.87 13.9   9  54 3.2e-11        0.73        0.96
Average_fixed_raters    ICC3k 0.93 13.9   9  54 3.2e-11        0.85        0.97

 Number of subjects = 10     Number of Judges =  7
See the help file for a discussion of the other 4 McGraw and Wong estimates,

この結果から以下のようにICC(3)の結果のみ取り出します。

# 全体のICC(3)を計算
whole_icc <- ICC(score_data)$results %>% 
  filter(type == "ICC3") %>% 
  pull(ICC)

print(whole_icc)

結果

[1] 0.6474741

審査員別の信頼性を評価する

ICCは0から1の範囲の値をとり、1に近いほど評価者間の評価の信頼性が高いことを示します。言い換えると、信頼性の低い評価者がいなくなると、全体のICCの数値は高くなります。そこで、評価者を順に1人ずつ除外してICCを計算し、各評価者が全体の信頼性にどのように影響しているかを確認します。

# 審査員を1人ずつ減らしてICC(3)を計算
judges <- colnames(score_data)
for (judge in judges) {
  ICC_res_tmp <- score_data %>% 
    select(- judge) %>% 
    ICC()
  ICC_res_tmp <- ICC_res_tmp$results %>% 
    filter(type == "ICC3") %>% 
    pull(ICC)
  
  ICC_score <- append(ICC_score, ICC_res_tmp)
}

# 各審査員のICC(3)スコアをデータフレームにまとめる
ICC_res <- data.frame(審判 = judges, ICC_score = ICC_score)

# 各審査員のICC(3)スコアを棒グラフで可視化し、全体のICC(3)を破線で表示
ggplot(ICC_res) +
  geom_bar(aes(x = 審判, y = ICC_score), stat = "identity") +
  geom_hline(yintercept = whole_icc, linetype = "dashed", color = "red", size = 1) +
  coord_flip() +
  xlab("") +
  theme(text = element_text(size = 12))

審査員を1人ずつ除外してICCを計算した結果がこちらです。例えば、judge_Aはその審査員を除外した時のICC(3)の値を示しています。
赤線は審査員全員のICCの値です。

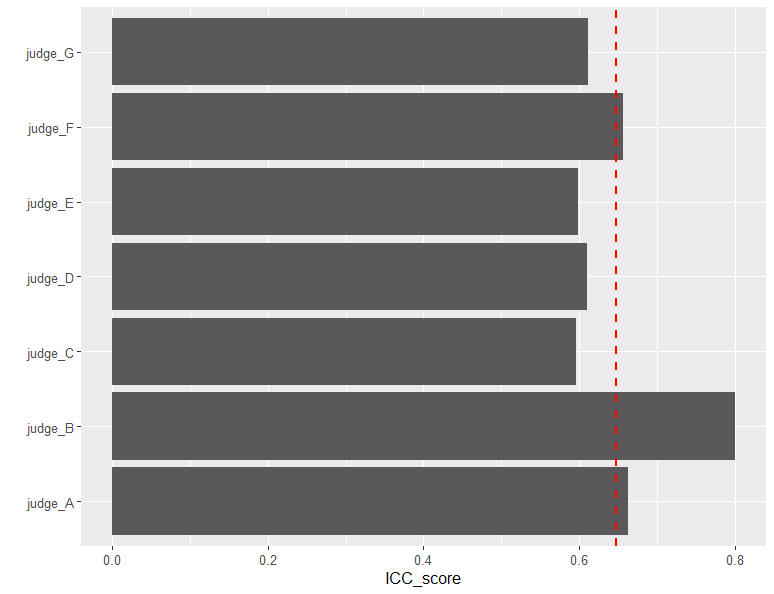
元々、審査員Bに大きなノイズを乗せたデータを生成していましたが、審査員Bを除外した時のICCが高くなっています。
つまり、審査員Bは信頼性の低い審査員といえます。
一方、審査員C、D、E、Gを除外した場合はICCの値が低下しているため、これらの審査員は信頼性が高いと判断できます。

おわりに

今回はICCを用いて、M-1グランプリのような審査員が漫才グループに対して審査することを想定しましたが、例えば実務を想定すると、複数の検査機器の信頼性を評価する場合にも有用です。
検査機器の信頼性評価にはICC(2)を使用し、特定の年数が経過した後に信頼性が低下する場合、その年数を閾値として設定することで、信頼性の一般化を判断することも可能です。
数理的な面も含めてさらに詳しく知りたい方は、こちらの論文も見てください。ICC1, ICC2, ICC3のそれぞれのガイドラインについて言及されています。
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4913118/pdf/main.pdf