形式言語理論における３つの『密』概念

• 6/17 更新 (自然密度を強化した「密度」の導入)
• 8/ 7 更新 (タイトル画像を挿入 (フォントは昭和書体さんの「陽炎書体」))

はじめに

形式言語理論は語(文字列)の集合，すなわち言語，を対象にさまざまな方向から解析する学問です．
プログラミングの世界においても正規表現や構文解析，さらにはモデル検査など，様々なところで形式言語理論の成果の恩恵が潜んでいます．

言語の素朴な性質としてその大きさ --あるいは「如何に密か」-- を測る概念はいくつかあるのですが，本稿では流行りに乗って３つの「密」概念を紹介したいと思います．ざっくりいうとそれぞれ確率的・位相的・組合せ的な「密」の尺度となっています．形式言語理論の三密に慣れ親しんでみてください(実世界では三密は避けて！)．

以下，文字の集合として大文字$A$を，$A$上の語全体の集合を$A^*$，$A$上の長さ$n$の語全体の集合を$A^n$と記します．
また，集合$S$に対して $\#(S)$ で$S$の要素数を表すこととします．
例えば$\#(A^n) = \#(A)^n$が成り立ち，$A = \{a,b\}$ の場合は$ \#(A^n) = 2^n$となります．

その１：確率的な「密」

ランダムに生成した語がことごとく言語 $L$ に属するとき，$L$ は「大きい」あるいは「密である」という素朴な直感があります．
長さ$n$のランダムに生成した語が $L$ に所属する確率は

\frac{\text{長さ$n$の$L$に属する語の総数}}{\text{長さ $n$ の語の総数}} = \frac{\#(L \cap A^n)}{\#(A^n)}

と素朴に表せますが，この確率の $n$ に対する極限を取った値を言語$L$の自然密度(natuarl density)と呼び $\delta(L)$ で表します

\delta(L) = \lim_{n \rightarrow \infty} \frac{\#(L \cap A^n)}{\#(A^n)}

例えば正規表現 $aa (a|b)^* $ (あるいは$A = \{a,b\}$のとき単純に $aa A^* $ とも書きます) に(完全)マッチする語の全体は「先頭が $aa$ である $A = \{a,b\}$ 上の語の全体」となります．
先頭の2文字は $aa, ab, ba, bb$ の4種類なので，$\delta(aa (a|b)^*) = 1/4$ であることがわかります．
また，いわゆる無限の猿定理 は比喩的に

「猿がタイプライターの鍵盤をいつまでもランダムに叩きつづければ、ウィリアム・シェイクスピアの作品を打ち出す」 (Wikipediaより)

と表現される定理ですが，自然密度を使うと

• 定理(無限の猿)：任意の語 $w$ について $\delta( A^* w A^* ) = 1$ が成り立つ．

と形式的に簡潔に言い表すことができます(非形式的な比喩表現も素敵ですが)．
$ A^* w A^* $つまり「$w$ を部分語として含む語全体」という形の言語がとても大きい(ほとんど全ての語を含む)ということを言っているのが無限の猿定理です．

自然密度は単純な分数の極限なので計算しやすいですが，言語によっては極限が収束しない場合もあります．例えば $(AA)^* = \{ w \in A^* \mid \text{$w$の長さは偶数}\}$の用な言語の場合

\frac{\#((AA)^* \cap A^n)}{\#(A^n)} = \begin{cases}
1 & n\text{が偶数}\\
0 & n\text{が奇数}
\end{cases}

となり収束しません．とはいえ感覚的には「長さが偶数か否か」は気持ち的には確率$1/2$になってほしいでしょう．その気持を素朴に形式化したのが，自然密度をより収束しやすい形に変形したの密度$\delta^*$という概念になります

\delta^*(L) = \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k = 0}^{n-1} \frac{\#(L \cap A^k)}{\#(A^k)}

こうすると$\delta((AA)^* )$は収束しませんが，$\delta^* ((AA)^* ) = 1/2$が成り立ちます．
言語 $L$ の自然密度が収束する場合は必ず $\delta(L) = \delta^* (L)$ が成り立つため，密度は自然密度を自然に拡張した概念となっています．自然密度の方が計算が楽なので，自然密度が収束する場合は$\delta^*(L)$よりも$\delta(L)$を計算したほうが良いでしょう．

さて，無限の猿定理に話を戻します．
言語$L$がある語$w$に対して$A^* w A^* \subseteq L$となっている場合，無限の猿定理より $A^* w A^* $ はとても大きいので，それを含む$L$もとても大きはずです．実際，この場合には$\delta(L) = 1$が素朴に成り立ちます．
補集合の視点から見ると，$A^* w A^* \subseteq L$となっているときには$L$の補集合$\overline{L}$では$\overline{L} \cap A^* w A^* = \emptyset$となっています．
一般に，言語 $L$ に対して $L \cap A^* w A^* = \emptyset$ となるような語を$L$の禁句と呼びます．禁句という言葉を用いると，無限の猿定理は

• 定理(無限の猿)：言語 $L$ が禁句を持つ場合は $\delta( L ) = 0$ が成り立つ．よって $\delta^*(L) = 0$も成り立つ．

と言い換える事ができます．$\delta^* ( L ) = 0$ となるような言語は直感的には「まったくすかすかな言語」なわけですから，極端に小さな言語です．このような言語を零(null)な言語と呼ぶこととします．逆に零でない言語を非零(non-null)と呼ぶこととしましょう．

形式言語理論における最初の密概念はこの「非零」な言語になります．「ある程度スカスカでない言語」はある程度は密であると素朴に考えられるでしょう．$ A^* w A^* $ のように自然密度が1であるような言語は密な言語のなかでも極端に密な存在です．$aa (a|b)^*$ で表現される言語はそこまで密ではないものの，スカスカとは言い難いでしょう．

その２：位相的な「密」

次の「密」概念はすでに紹介した「禁句」を使って簡潔に言い表すことができます．
ずばり，禁句を一切持たない(すなわち任意の語を部分語として含む)言語のことを稠密(dense)であると言い，こちらが2つめの位相的な「密」概念となります．

これをなぜ「位相的」と呼ぶのでしょうか？その点を説明していきたいと思います．
位相空間論において位相空間$X$の部分集合$S$が$X$において稠密であるとは，$X$の任意の元$x$についてその近傍と$S$が交わりを持つことを言います．同値な定義として「$S$の閉包($S$を含む最小の閉集合)が$X$となる」という言い換えがありますが，これは言語の場合において直感的には「$L$の部分語全体の集合 $ \{ v \mid uvw \in L \text{ for some } u,w \}$ が $A^* $ となる」すなわち $L$ が稠密であるということに対応します．実際，$A^* $という空間に$A^* w A^* $あるいは空集合を開基として考えれば$A^*$に位相が入り言語 $L$ が「禁句を持たない」という意味で稠密であることと $L$ が位相の意味で稠密であることは一致します．

無限の猿定理より，禁句を持つ言語は密度$0$なので，位相的な意味で「密」でない言語は確率的な意味でも「密」でないことがわかります．
しかし，その逆は一般には成り立ちません．
例えば「$a$と$b$の出現回数が等しい語全体」= $ \{ \varepsilon, ab, ba, aabb, abab, abba, baba, bbaa, aaabbb, \ldots \} $ は禁句を持ちませんが密度は$0$すなわち零言語となります．

一方，正規表現で表現できる語の集合，つまり正規言語について2つの「密」概念が一致することが知られています．

• 定理(S. 2015)： 任意の正規言語 $L$ について，「$L$が非零である」と「$L$が稠密である」は同値．

その３：組合せ的な「密」

任意の語$w \in A^* $が言語 $L$ の要素のたかだか $k$ 個の連接で表現できるとき，$L$ を基(basis)と呼びます．また，そのような最小の $k$の値を基$L$の位数と呼びます．

例えば簡単な例として言語 $L_k = \{ w \in A^* \mid |w| = 1 \mod k \} = $「長さが$\mod k$で1の語全体」を考えると，これは位数$k$の基となります．
この言語$L_k$は稠密かつ非零な言語です．自然密度は収束しません($1$と$0$を振動する)が，なんにせよ密度は$0$にはなりません．

一般に稠密でない言語$L$は基にはなりえません．

• 定理：稠密でない言語$L$について，$L$は基にならない．さらに，任意の$k$に対して$L^k$は零となる．

なぜかと言うと，稠密でない$L$は定義より$A^* w A^* \cap L = \emptyset$となる語$w$が存在しますが，その場合任意の$k \geq 1$に対して $L^k = \{ w_1 w_2 \cdots w_k \mid w_i \in L \text{ for all } i \}$も$w^k$を禁句として持ち稠密になりません．
というのも，$L^k$が$w' = x w^k z$となる語$w'$を含んでいると仮定すると，$w'$の任意の$k$個の分割$w' = w_1 w_2 \cdots w_k$について少なくとも1つの$w_i$が$w$を部分語に含むはずで$L$に属するある語が$w$を含むこととなり，$L$が$w$を禁句に持つことと矛盾します．
そのため無限の猿定理より$L^k$は零言語となり，その有限和である「$L$の要素のたかだか$k$個の連接」$= \{\varepsilon\} \cup L \cup L^2 \cup \cdots \cup L^k$も密度が零の零言語となります．全ての語の全体$A^* $は密度1で当然零言語ではないため，「$L$の要素のたかだか$k$個の連接」が$A^*$になることはありません．

この定理は言語が位相的には「密」でないと(稠密でないと)基にはなりえないことを言っています．
その一方，実は確率的には「密」でない言語(零言語)は基になる場合があります．

定理：密度0の基が存在する．

証明は加法的整数論の結果を使うことで簡単に示せます．
例えば言語として$L_{sq} = \{ w \in A^* \mid |w| = n^2 \text{ for some } n \in \mathbb{N} \}$すなわち「長さがある数の二乗になる語の全体」を考えると，四平方定理より任意の自然数$n \in \mathbb{N}$(0を含む)はたかだか4つの平方数の和であるため，$L_{sq}$は位数4の基となります．

\frac{\#(L_{sq} \cap A^n)}{\#(A^n)} = \begin{cases}
1 & n \text{が平方数}\\
0 & \text{それ以外}
\end{cases}

が成り立つため，$L_{sq}$は自然密度を持ちません．その一方，「$n$未満の平方数の個数」は $\sqrt{n}+1$以下である¹ため，

\frac{1}{n} \sum_{k = 0}^{n-1} \frac{\#(L_{sq} \cap A^k)}{\#(A^k)} \leq \frac{\sqrt{n}+1}{n} = \frac{1}{\sqrt{n}} + \frac{1}{n}

が成り立ち，その極限 $\delta^* (L_{sq})$は$0$に収束します．すなわち$L_{sq}$は密度$0$の零言語です．

逆に，非零であれば必ず基になるかと言うとそんなことはありません．例えば$a A^* b$($a$で始まって$b$で終わる語全体)のような正規言語が単純な反例となります．
先に述べたとおり，正規言語に限ると非零と稠密という概念は一致するため次の定理が成り立ちます．

• 基となる正規言語は必ず非零．

すなわち$L_{sq}$のような例は必ず正規言語の外の世界で起こるということです．

まとめ

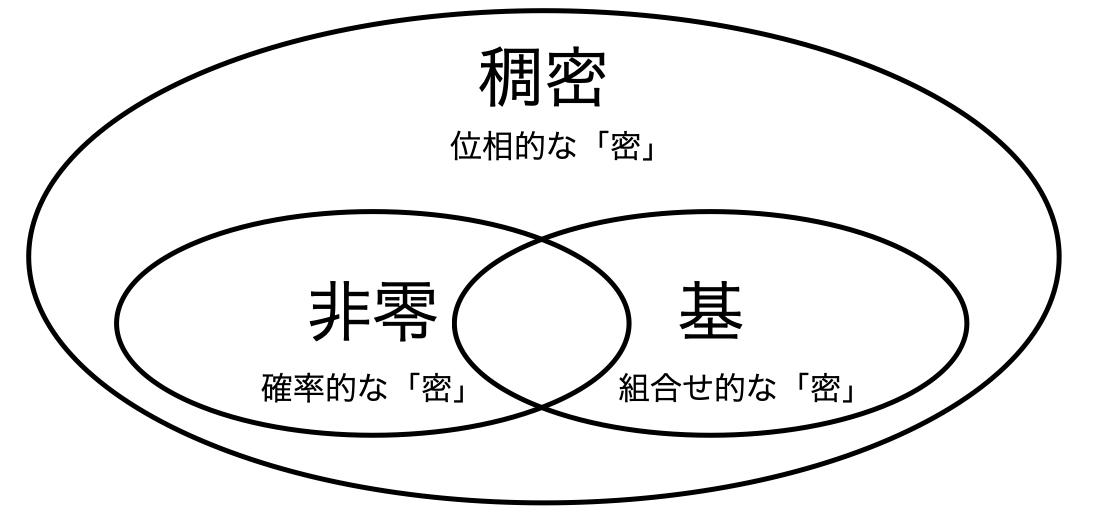
３つの「密」概念の関係はそれぞれ以下の図のような包含関係となっています．

非零という「密」概念は稠密という「密」概念に真に包含されます(すなわち任意の言語について「非零ならば稠密」が成り立つが逆は成り立たない)．
その一方，正規言語の世界に限ると両者は完全に一致します．形式言語理論の世界ではしばしばこういった現象が起こります．
意味的に異なる概念が乱立する世界も面白いですが，個人的には「一見異なるように見えるが一致する概念」が好きなことが多く，正規言語の世界ではたびたびそういった現象が垣間見れて楽しいです．

稠密という概念については符号理論の文脈から昔からいろいろ研究されていたようです．興味のある方は文献²を読まれると良いかもしれません．言語の自然密度についても文献²でよく議論されています．
先の定理(S. 2015)の証明は拙著サーベイ³を御覧ください．

基という３つ目の「密」概念はもともと加法的整数論における加法的な基を本稿のために私が勝手に形式言語版に拡張した概念です．
形式言語理論においては基という概念は(ちゃんとサーベイしてませんが私の知る限りは)特に研究対象になっていないようです．そもそも加法的な基ですらいろいろな難問揃いなのに，その形式言語版の拡張で有意義な理論的結果が得られるかどうかは良くわかっていません⁴．

1. $0 = 0^2$も平方数としてカウントしています． ↩

2. Berstel et al: Codes and Automata ↩ ↩²

3. 新屋良磨：オートマトン理論再考 ↩

4. 加法的整数論勉強したい... ↩