この記事について
これは Supership Advent Calendar 2018 16日目です。
この記事では、広告/デジタルマーケティング系の企業に務めるデータサイエンティスト/データアナリスト向けに、以下の項目を記述します。
- ポアソン分布に従う事象
- カウント値Nに対する統計的ゆらぎ
- 単純な比の統計ゆらぎ (e.g. 男女比, リフト値, etc.)
- 全体に対する割合の統計的ゆらぎ (e.g. CTR, CVR, 10代男性の割合, etc.)
できるだけ数式の意味や使い方について詳しく記述するようにしており、厳密な数学的証明などは書いてません。
はじめに
どうも。sinoue1106です。大学院博士後期課程で博士号を取得後、2018年4月から(いちおう)新卒で広告系企業のデータサイエンティストとなったものです。大学院の時の専門は天体物理学で、放射線検出器作って、宇宙に打ち上げて、観測したデータを分析して、論文書く、みたいなことしてました。入社してからの分析業務で、大学院時代で培った統計学/放射線計測学の知識が役に立つことがあったので、この記事を書くことにしました。
インターネット広告/デジタルマーケティングの業務で出てくる数字は、確率的に変動するものが多いです。でてきた値がどのくらいの範囲で確率的にゆらぎうるのか、以下を読めば計算できるようになります。
ポアソン分布に従う事象
離散的な自然現象(0回、1回、2回...と発生する現象)の発生確率はポアソン分布に従います
(ポアソン分布の詳しい説明はWikipediaをご覧ください)。
以下は、ポアソン分布に従う事象の例です。
- ある交差点を通過する1時間あたりの車両数。
- 単位時間あたりの放射線の計数値
- 1立方光年あたりの恒星の数
- 1分間のWebサーバへのアクセス数
- 1日に受け取る電子メールの件数
- 広告配信におけるimpression, clickの数
広告/マーケティング系の企業で扱う数字は、ポアソン分布に従う場合が多いです。
カウント数に対する統計的ゆらぎ
ポアソン分布に従う事象をカウントしたら$N$でした。
このカウント数$N$に対する統計的ゆらぎ(統計誤差)は
\sigma_N = \sqrt[]{N}\ \ \ \ \ \ \ \ \ \cdots(1)
で計算できます。これは、68%の値でゆらぐ範囲です。
(数学的な証明は、ここがわかりやすいです)
例えば、ある期間アンケートを実施し回答してくれた20代男性の数が10,000人だった場合、$\sigma_N = \sqrt[]{10,000}=100$です。同じ条件で、再びアンケートを取った時、68%の確率で9,900~10,100人の範囲内になるといえます。
また、カウント数に対するゆらぎの相対値(相対誤差)は
\frac{\sigma_N}{N}=\frac{1}{\sqrt[]{N}}
と表されます。これは、得られた計測値に対して、10倍小さくして正確な議論がしたければ、100倍のVolumnが必要なことを示します。
ただし、式(1)の適用は、ポアソン分布が正規分布に近似できる時に限ります。$N$が10,20以下の時、この事象が従うポアソンの確率分布を正規分布を近似できないので、式(1)を適用できないので、注意しましょう。
誤差(ゆらぎ)の伝播則
ある値を複数個計測できたら、それらを演算したい時があります。たとえば、あるアンケートを実施して、男性、女性の数が$N_{\rm M}$、$N_{\rm W}$だったとき、これらの数字の統計的ゆらぎは式(1)で求められますが、男女比$R=N_{\rm M}/N_{\rm W}$の値につく統計ゆらぎはどう計算されるでしょうか。
zという量がxとyによって計算される、つまり、
z = f(x, y)
のような関係にある場合、$z$の誤差$\sigma_z$は、$x$、$y$の誤差$\sigma_x$、$\sigma_y$, $x$と$y$の共分散$\sigma_{xy}$を用いて、
\sigma_z = \sqrt[]{\left(\frac{\partial z}{\partial x}\sigma_x\right)^2 + \left(\frac{\partial z}{\partial y}\sigma_y\right)^2 + 2\sigma_{xy}\left(\frac{\partial z}{\partial x}\right) \left(\frac{\partial z}{\partial y}\right)}\ \ \ \ \ \ \cdots(2)
と表されます。
$x$と$y$が独立な場合(相関していない場合)、ルート内の第三項は0となるので、
\sigma_z = \sqrt[]{\left(\frac{\partial z}{\partial x}\sigma_x\right)^2 + \left(\frac{\partial z}{\partial y}\sigma_y\right)^2}\ \ \ \ \ \ \cdots(3)
と表されます。
誤差の伝播則について、もっと詳しく知りたい方は、このqiita記事とかを参照してください。
単純な比の統計的ゆらぎ
ここでいう「単純な比」というのは、分母と分子にくる量が独立な関係(相関していない関係)にある場合の比を意味してます。例えば
- ある集団の男女比
- Aという広告配信のCTRと, Bという広告配信のCTRの比
などです。
式(3)を適用すると、$r=f(x,y)=x/y$の統計ゆらぎは、
\sigma_r=r\ \sqrt[]{\left(\frac{\sigma_x}{x}\right)^2 + \left(\frac{\sigma_y}{y}\right)^2}
と計算できます。
(例題1)
ある広告をclickした人の数が、男性$N_{\rm m}=4000$、 女性$N_{\rm w}=8000$だった時、それぞれの統計誤差は、$\sigma_{N_{\rm m}}=\sqrt[]{4000}\simeq63.2$、$\sigma_{N_{\rm m}}=\sqrt[]{8000}\simeq89.4$程度です。よって、ある広告をclickした男女比$r=N_{\rm m}/N_{\rm w}=0.5$につく統計誤差は
\sigma_r=0.5\ \sqrt[]{\left(\frac{63.2}{4,000}\right)^2 + \left(\frac{89.4}{8,000}\right)^2}
\simeq0.01
程度になります。($r=0.50\pm0.01$)
0.49~0.51が68%の確率でゆらぎうる範囲ということになります。
(例題2)
ある商品の購買者の年代別の割合とその誤差が、group Aと全体で以下の表となる。
| 10代 | 20代 | 30代 | 40代 | 50代 | 60代 | ||
|---|---|---|---|---|---|---|---|
| group A | 割合(%) | 9 | 19 | 25 | 19 | 11 | 17 |
| 誤差(%) | 2 | 3 | 3 | 3 | 2 | 3 | |
| 全体 | 割合(%) | 11.1 | 15.1 | 19.7 | 23.6 | 18.0 | 12.5 |
| 誤差(%) | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
(※ 順番が前後しますが、全体に対する割合の誤差の求め方については、次節で説明します)
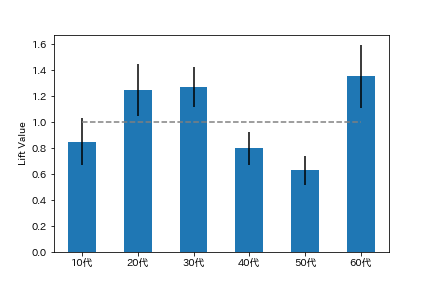
この時、リフト値とその統計的ゆらぎを可視化したい場合、以下のようになる。
import pandas as pd
from math import sqrt
import matplotlib.pyplot as plt
#%matplotlib inline # jupyter-notebook環境の場合、アンコメント
# テーブルの数値
list_A_val = [9.4, 18.8, 25.0, 18.8, 11.3, 16.9]
list_A_err = [2, 3, 3, 3, 2, 3]
list_all_val = [11.1, 15.1, 19.7, 23.6, 18.0, 12.5]
list_all_err = [0.2, 0.2, 0.2, 0.2, 0.2, 0.2]
list_lift = list()
list_lift_err = list()
for A_val, A_err, all_val, all_err in zip(list_A_val, list_A_err, list_all_val, list_all_err):
lift = A_val/all_val # リフト値を計算
err = lift*sqrt((A_err/A_val)**2+(all_err/all_val)**2) # リフト値の誤差を計算
list_lift.append(lift)
list_lift_err.append(err)
ix = ['10代', '20代', '30代', '40代', '50代', '60代']
df_val = pd.DataFrame({'group A': list_lift}, index=ix)
df_err = pd.DataFrame({'group A': list_lift_err}, index=ix)
df_line = pd.DataFrame({'group A': [1, 1, 1, 1, 1, 1]}, index=ix) # 補助線
ax = df_val.plot.bar(yerr=df_err, legend=False)
df_line.plot(linestyle='--', legend=False, color='grey', ax=ax).set_ylabel("Lift Value")
plt.show()
リフト値が1(補助線)からどれだけリフトしているか、ゆらぎの範囲といっしょにわかりやすく可視化されました。
全体に対する割合の統計ゆらぎ
次に全体に対する割合の統計ゆらぎの計算方法です。具体的には、
- CTR (総impression中のclickの割合)
- CVR (全母数のうちのconversionの割合)
- ある集団の全体に対する10代の割合
などの統計的ゆらぎを計算したい場合です。
これは、$z=x+y$の関係にある時の、$r=x/z$の統計ゆらぎを求めることです。前節と同じ比の計算なのですが、このとき注意しないといけないのが、分母の$z$と分子の$x$が相関していることです。このような場合は、式(3)を適用してしまうと、共分散の項の分だけ間違えてしまいます。共分散を求めるのは少し面倒なのでなるべく式(2)ではなく式(3)を使いたいです。こういった場合は、相関していない数に置き換えて考えるとこの問題は避けられ、式(3)を適用できます。今回のケースだと
r=f(x,y)=\frac{x}{x+y}
として考えると、式(3)を適用でき、
\sigma_r=\frac{xy}{(x+y)^2}\sqrt[]{\left(\frac{\sigma_x}{x}\right)^2 + \left(\frac{\sigma_y}{y}\right)^2}
と計算できます。
(例題3)
ある広告配信を一定の期間実施した時、impression数が$N_{\rm i}=500000$, clickが$N_{\rm c}=400$だった時、それぞれの統計誤差は、$\sigma_{N_{\rm i}}=\sqrt[]{500000}\simeq707$、$\sigma_{N_{\rm m}}=\sqrt[]{400}\simeq20$程度です。よって、ある広告のclick率$r_{\rm c}=N_{\rm c}/N_{\rm i}=0.0008$につく統計誤差は
\sigma_{r_{\rm c}}=\frac{499600\cdot400}{(499600+400)^2}\ \sqrt[]{\left(\frac{707}{499600}\right)^2 + \left(\frac{20}{400}\right)^2}
\simeq0.00004
程度になります。($r_{\rm click}=0.00080\pm0.00004$)
0.00076~0.00084が68%の確率でゆらぎうる範囲ということになります。
(例題4)
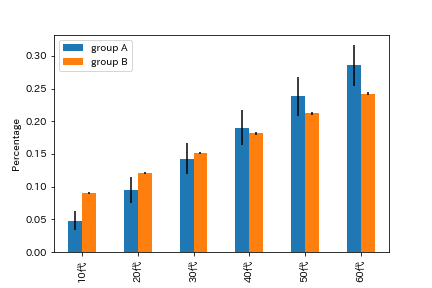
ある集計をした時、groupA, Bに含まれる人数が、年代別で以下だった。
| 10代 | 20代 | 30代 | 40代 | 50代 | 60代 | |
|---|---|---|---|---|---|---|
| group A | 10 | 20 | 30 | 40 | 50 | 60 |
| group B | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 |
各グループにおける年代の含有率とその統計的ゆらぎを可視化したければ、以下のようになる。
import pandas as pd
from math import sqrt
import matplotlib.pyplot as plt
#%matplotlib inline # jupyter-notebook環境の場合、アンコメント
# テーブルの数値
list_num_A = [10, 20, 30, 40, 50, 60]
list_num_B = [3000, 4000, 5000, 6000, 7000, 8000]
# リストを与えた時、各要素の全体に対する割合と統計誤差を返す関数を定義
def gen_frac_error(list_num):
list_frac = list()
list_error = list()
for num in list_num:
sum_num = sum(list_num)
num_not = sum_num - num # 対象の要素以外の合計
frac = num/sum_num # 全体に対する割合の計算
error = num*num_not/(num+num_not)**2*sqrt((sqrt(num)/num)**2 + (sqrt(num_not)/num_not)**2) # 誤差の計算
list_frac.append(frac)
list_error.append(error)
return list_frac, list_error
list_frac_A, list_error_A = gen_frac_error(list_num_A)
list_frac_B, list_error_B = gen_frac_error(list_num_B)
ix = ['10代', '20代', '30代', '40代', '50代', '60代']
df_data = pd.DataFrame({'group A': list_frac_A, 'group B': list_frac_B}, index=ix)
df_error = pd.DataFrame({'group A': list_error_A, 'group B': list_error_B}, index=ix)
df_data.plot.bar(yerr=df_error).set_ylabel("Percentage")
plt.show()
まとめ
- ポアソン分布に従う現象のカウント数$N$の統計ゆらぎは
\sigma_N = \sqrt[]{N}
- x,yが相関していない場合、$r=x/y$の関係にある統計ゆらぎは以下。男女比やリフト値などに適用しましょう。
\sigma_r=r\ \sqrt[]{\left(\frac{\sigma_x}{x}\right)^2 + \left(\frac{\sigma_y}{y}\right)^2}
- $z=x+y$の関係にある時の、$r=x/z$の統計ゆらぎは以下。CTR, CVR, 全体に対する10代の割合などに適用しましょう。
\sigma_r=\frac{xy}{(x+y)^2}\sqrt[]{\left(\frac{\sigma_x}{x}\right)^2 + \left(\frac{\sigma_y}{y}\right)^2}