はじめに
PRMLを参考にしながら、ベイズの定理を図示してみました。
ベイズの定理の式
任意の確率変数を$ X,Y $とすると、以下の式がなりたちます。
$$ P(Y | X) = \frac{P(X|Y)P(Y)}{P(X)} $$
ここで$P(Y|X)$はXが起こった時にYが起こる確率で、$P(X|Y)$はYが起こった時にXが起こる確率を表しています。
、、、とは言ったものの、なぜこの式が成り立つのかイメージしずらいですよね。(少なくとも私はそうでした...)
なので、なるべく図を用いてこの式を紐解いて行こうと思います。
それぞれの確率の図示
具体的な例として、以下のような黒い玉と白い玉が入っている赤箱、青箱、黄箱、緑箱がある状況を考えてみます。

これらの箱から玉を取り出す場合、どの箱を選ぶか、どの玉を選ぶか、という二つの選択が必要です。これらの二つの選択がそれぞれ確率変数$X,Y$とすると、以下のように表すことができます。
$$ X = {青箱,赤箱,黄箱,緑箱}$$
$$ Y = {黒玉,白玉} $$
この状況の中で、目を閉じて玉をどれかの箱から取り出したら、黒玉が出てきました。この時、選んだ箱が黄箱である確率$P(X=黄箱|Y=黒玉)$を求めてみましょう。
まず、確率変数$X,Y$の具体数ををまとめてみます。
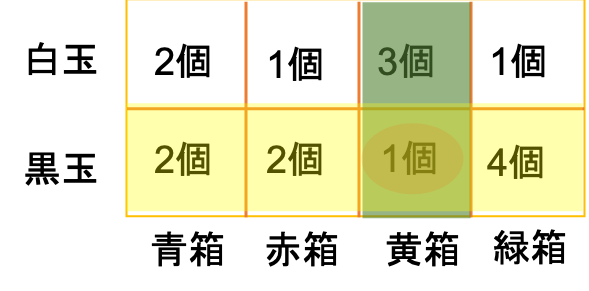
ここで、黄箱に含まれる玉の個数を緑の網かけ、黒玉の全数を黄色の網かけ、黄箱かつ黒玉を選ぶ個数を赤丸で表します。すると、黒玉を選んだ時に、黄箱である確率は以下のように表せます。
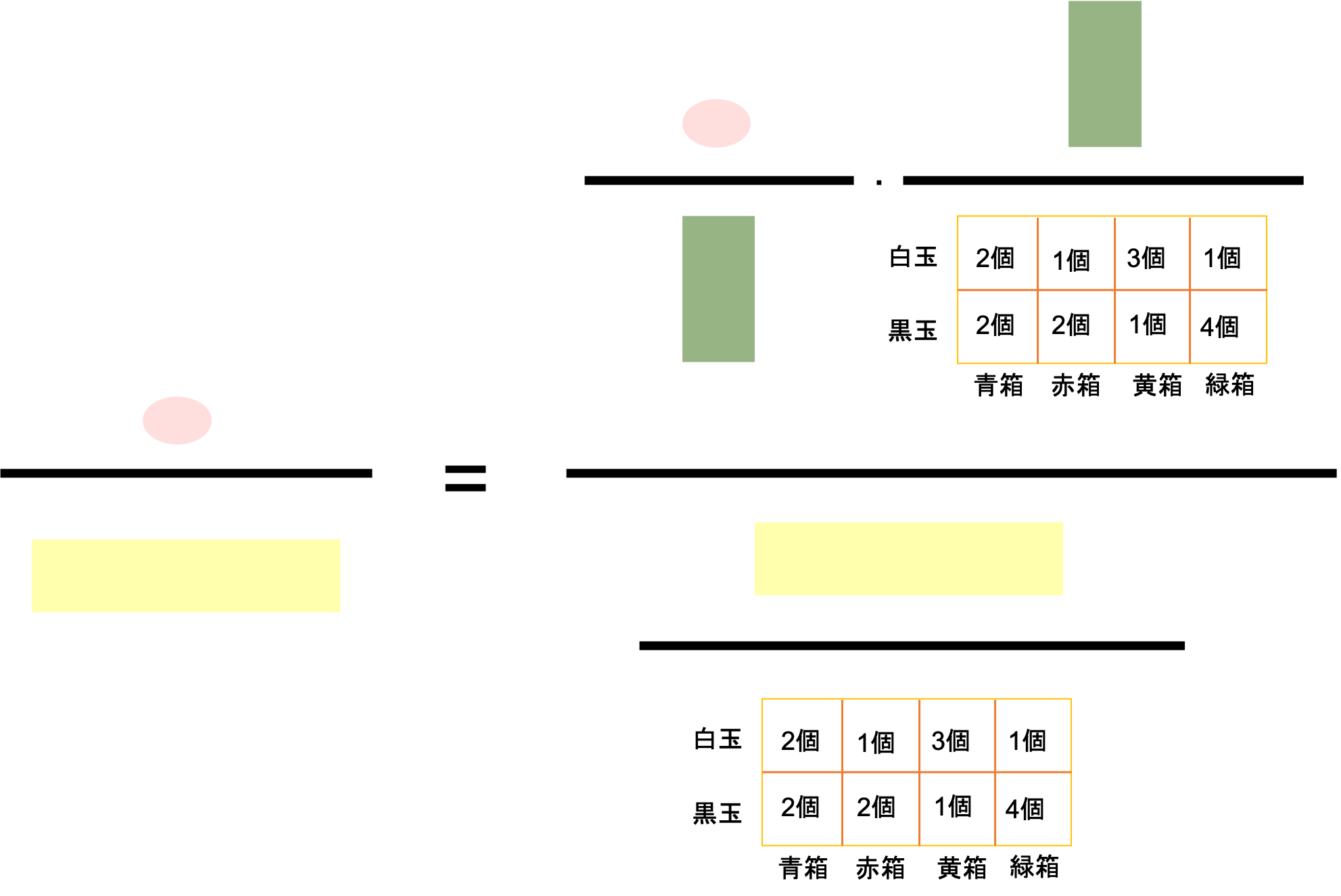
ここで、オレンジ色の格子は全ての玉の数となります。
上図を式で表すと以下のようになります。
$$ P(X=黄箱|Y=黒玉)=\frac{P(Y=黒玉|X=黄箱)P(X=黄箱)}{P(Y=黒玉)} $$
実際に計算すると以下のようになります。
$$ P(X=黄箱|Y=黒玉)=\frac{\frac{1}{4}\frac{4}{16}}{\frac{9}{16}}=\frac{1}{9}$$
終わり
最後の方が駆け足になってしまったので説明が雑になってしまいました。もっと研鑽します、、、