初めに

テキストの分析をたまにするのですが、編集距離を求める場面があります。
今回はその編集距離を自分で実装し、計算量を調べてみます。

編集距離(Levenshtein Distance)とは

Wikipediaより引用します

レーベンシュタイン距離（レーベンシュタインきょり、英: Levenshtein distance）は、二つの文字列がどの程度異なっているかを示す距離の一種である。編集距離（へんしゅうきょり、英: edit distance）とも呼ばれる。具体的には、1文字の挿入・削除・置換によって、一方の文字列をもう一方の文字列に変形するのに必要な手順の最小回数として定義される

まずはライブラリを利用してどんな感じか見てみましょう。
今回はjellyfishというPythonのライブラリをお借りし、jellyfishとsmellyfishの編集距離を計算してみます。

In [1]: import jellyfish

In [2]: jellyfish.levenshtein_distance(u'jellyfish', u'smellyfish')
Out[2]: 2

2という結果が出ました。これを手計算で検証しましょう。

上記の場合、jellyfishを、最短何手でsmellyfishに変換できるかを考えます。

jをmに置換
- このとき、jellyfish　→ mellyfish
先頭にsを挿入
- このとき、mellyfish　→ smellyfish

というわけで2手で変換ができ、ライブラリで計算した結果と一致しました。

編集距離の計算方法

編集距離は、DP（動的計画法）で計算されることが知られています。
まずは計算方法を説明します。

下記のサイトがとても分かりやすく、参考にさせて頂きました。

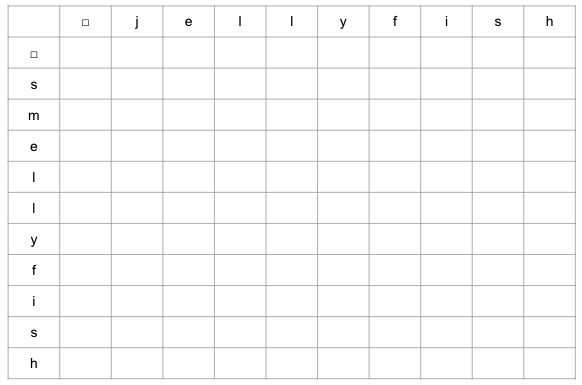
DPを使った計算方法

表を用意します。

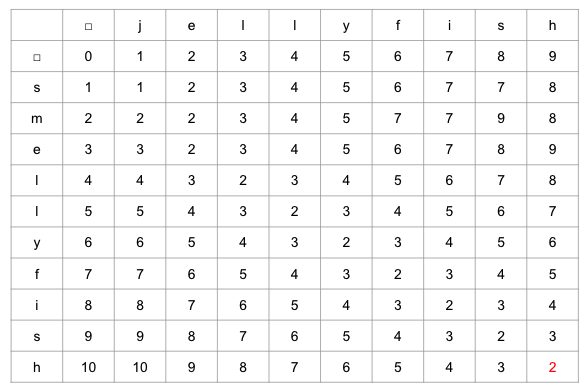
各マスには、対応する２つの部分文字列の編集距離を記載していきます。
1行目と1列目を埋めます。

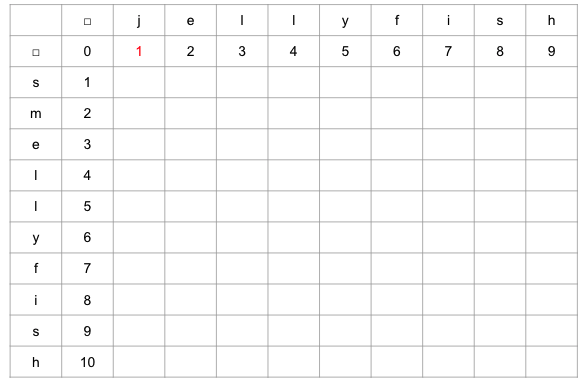
例えば、(行、列) = (□, j)の要素(赤文字部分)については、空文字□をjに変換するために必要な編集回数を入れます。空文字□をjに変換するためには、jを挿入すればいいため、その編集距離は1となります。他の部分も同様の計算で埋めていきます。
残ったマスの編集距離を、上、左から記載していきます。

下記３つの候補の最小値を、マスに入れます。
- 着目しているマスの、上のマスの編集距離＋１
- 着目しているマスの、左のマスの編集距離＋１
- 着目しているマスの、左上のマスの編集距離＋c
  - ただし、比較している行と列の文字が等しい場合はc=0, 異なる場合はc=1
DPでは計算量を減らすために、各文字における編集距離の最小値のみを保持し、次の文字の計算を行います。

ここはもう少し具体的に書かないと分かりづらいと思うため、「なぜDPだと計算量が減るのか」で詳しく説明します。

記載した結果は下記となります。右下の赤文字部分がjellyfishとsmellyfishの編集距離を表しており、2となります。この値は、ライブラリで計算した結果と一致しました。

なぜDPだと計算量が減るのか

一言で言うと、「各文字における編集距離の最小値のみを保持するから」です。
とは言ってもよく分からないと思うため、まずは全探索でjellyfishとsmellyfishの編集距離を求める場合を考えます。

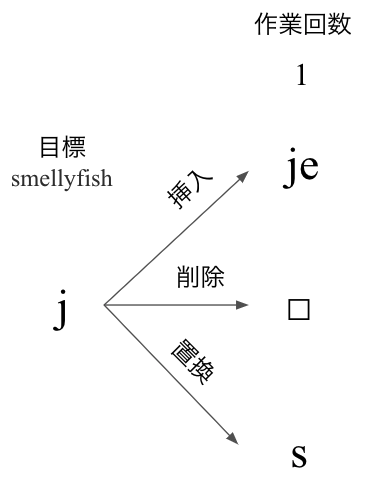
まずjellyfishのjについて考えます。可能な動作は挿入・削除・置換の３つあります。
図にすると下記のようなイメージになります。
(本来は何を挿入すべきか、何に置換すべきかについての話もありますが、今回は簡略化のため無視しています。)

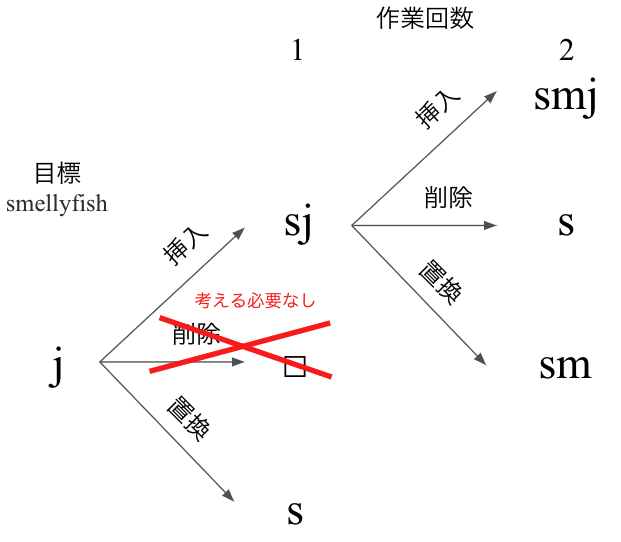
次に、挿入を行ったsjについて、更に挿入・削除・置換を行った場合を図示します。

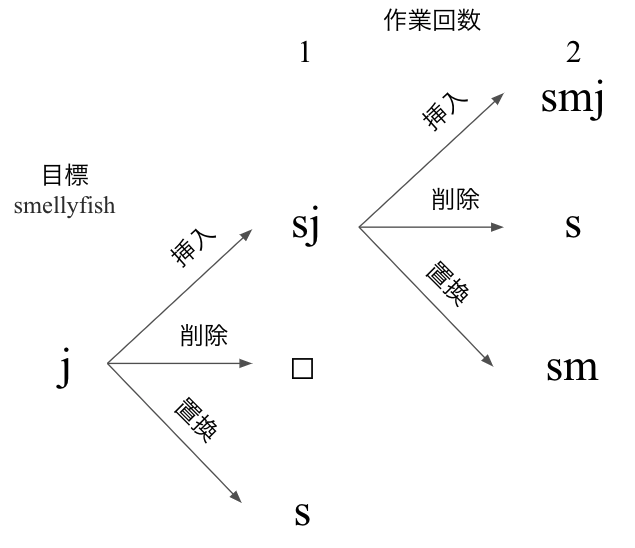
全探索の場合、これを継続することで全てのパターンを網羅し、最終的にsmellyfishへと変換できたパターンのうち、編集距離が最小のものを出力します。

計算量は、挿入・削除・置換という３つの作業を文字数分だけ行うため、文字数をnとした場合、O(3 ** n)となります。

ただ、明らかに考えなくて良いパターンがありますね。例えば、最初にjを削除した場合を考える必要はありません。何故なら、目標の文字に近づけるためには、挿入 or 置換の方が一文字分作業を減らすことができるためです。

つまり、各作業回数の中で、「目標とする文字への変換へと最も近い」＝「編集距離が最も小さい」パターンのみを計算すれば最終的な答えが求まることが分かります。

上記の考えを実現したのがDPです。

Pythonでの実装

上記に記載した内容をそのまま実装しています。
対象の二つの文字列は、それぞれs,tとして実装しています。

if __name__ == "__main__":
    s = input()
    t = input()

    inf = float("inf")

    # 文字の長さに、最初の空白文字の長さを加算する
    s_l = len(s) + 1
    t_l = len(t) + 1

    # テーブルを作成
    dp = [[inf] * s_l for _ in range(t_l)]

    # 1行目を埋める
    dp[0] = [i for i in range(s_l)]

    # 1列目を埋める
    for j in range(t_l):
        dp[j][0] = j

    # 2行2列目以降を埋める
    for i in range(1, t_l):
        for j in range(1, s_l):
            left = dp[i][j - 1] + 1
            upp = dp[i - 1][j] + 1
            if s[j - 1] == t[i - 1]:
                left_upp = dp[i - 1][j - 1]
            else:
                left_upp = dp[i - 1][j - 1] + 1

            dp[i][j] = min(left, upp, left_upp)

    # t_l, s_lは文字の長さのため、インデックスに変換するために-1を行う
    print(dp[t_l - 1][s_l - 1])

AIZU ONLINE JUDGEの編集距離の問題でACだったため、おそらく問題ないコードなのだと思います。

計算量

この方法での計算量は、二つの文字列の長さをそれぞれm, nとおくと、
下記の二重forループの部分でm×nの計算を行なっているため、O(mn)となります。

    for i in range(1, t_l):
        for j in range(1, s_l):

あんまり早くないですね。
より早く解く方法については下記の記事が参考になりそうでした。

おまけ　計算量の可視化

Pythonコードの計算量を何かしらの形で数値化したいなぁと考えていたところ、cProfileによる方法を教わりました。

cProfileで、今回のコードの計算時間を算出してみましょう。

❯ python -m cProfile -s tottime 1.py
2
         99 function calls in 0.000 seconds

   Ordered by: internal time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.000    0.000    0.000    0.000 1.py:2(main)
        1    0.000    0.000    0.000    0.000 {built-in method builtins.print}
       90    0.000    0.000    0.000    0.000 {built-in method builtins.min}
        1    0.000    0.000    0.000    0.000 1.py:2(<module>)
        1    0.000    0.000    0.000    0.000 1.py:13(<listcomp>)
        1    0.000    0.000    0.000    0.000 {built-in method builtins.exec}
        1    0.000    0.000    0.000    0.000 1.py:16(<listcomp>)
        2    0.000    0.000    0.000    0.000 {built-in method builtins.len}
        1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

上記のncalls(関数が何回呼ばれているか)列を見ると、minが90回呼ばれていることが分かります。minは２重forループの中の関数のため、やはり２重forループがボトルネックになりそうだなということが分かりました。

最後に

普段ライブラリとして使っているものを、自分で実装すると理解が深まって楽しいです。もし誤っている点があったら教えてもらえると助かります。

編集距離(Levenshtein Distance)の計算方法・計算量を考える

初めに