Go to Qiita Advent Calendar 2024 Top
LoginSignup
15
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@simonritchie

1次元のセルラー・オートマトンをPythonで試す

Posted at

TL;DR

  • セルラーオートマトンの計算モデルの説明について触れます。
  • 1次元のセルラーオートマトンの実装をPythonで進めて動かしてみます。
  • 過程で必要になる知識なども、忘れているものなどがあるので調べつつまとめます。

主な参考文献

また、上記書籍のgithubのリポジトリのコードもMITライセンスなので参照・利用させていただきますmm

※本記事では割愛した説明なども山ほどあるので、ALife関係の詳細は書籍をお買い求めください。

セルラー・オートマトンとは

格子状のセルと単純な規則による、離散的計算モデルである。計算可能性理論、数学、物理学、複雑適応系、数理生物学、微小構造モデリングなどの研究で利用される。非常に単純化されたモデルであるが、生命現象、結晶の成長、乱流といった複雑な自然現象を模した、驚くほどに豊かな結果を与えてくれる。
セル・オートマトン - Wikipedia

  • セル・オートマトンとも呼ばれます。
  • 自然界の模様（e.g., : 貝殻の模様）などで見られるような模様を生成します。
  • グリッド上でのデータを参照して、次の段階のデータが決まります（その連続で、結果として模様が生成される）。
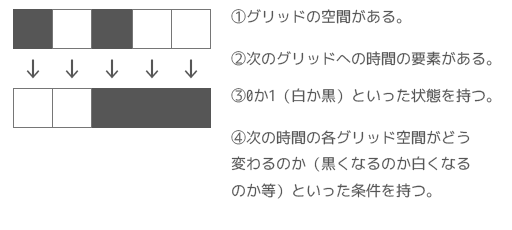
  • セルラー・オートマトンにはいくつも種類や条件がありますが、共通して以下のような条件を満たしています。
    1. グリッドの空間がある : 線としての1次元、面としての2次元、立体としての3次元のそれぞれのセルラー・オートマトンがあります。各次元とも、グリッドを参照して計算が実行されます。
    2. 時間が絡んでくる : 現在の状態を加味して、次の状態を生み出して・・・といったように、時間的な要因が絡んできます。
    3. グリッドの各セルが状態を持つ : 次の時間の結果を左右するパラメーターを、各セルが持ちます。
    4. 状態を加味して次の時間にどうなるか、の条件を持つ : 現在の各セルが○○の条件なので、次のセルは××になる、といったような条件を持ちます。

20190809_1.png

※普通色だと0が黒、1が白なイメージが強いですが、本記事の図なとではgithubのコードに合わせて1を黒、0を白として設定していきます。

今回の実装は、参考文献に合わせて以下のように対応します。

  • グリッド空間 : 1次元のセルラーオートマトンを対象とします。
  • 状態 : 0か1かの2値で扱います。
  • 条件 : 両隣と自身のセルの状態を参照して、次のセルの状態を決定します。

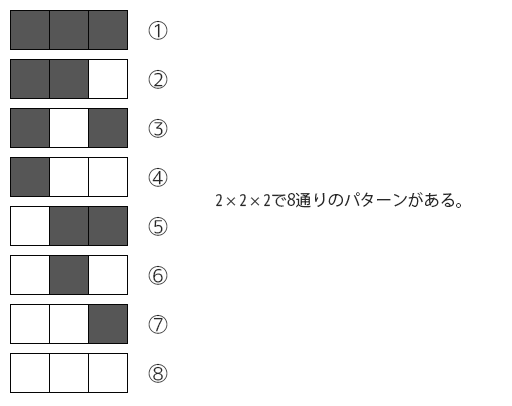
2値で3つのセルを参照するので、8つの組み合わせができる

0か1の2値で、左右と中央の3つのセルを参照して次の時間のセルの状態を決定するので、8つのパターンが存在します（$2^3$件のパターン）。

20190809_4.png

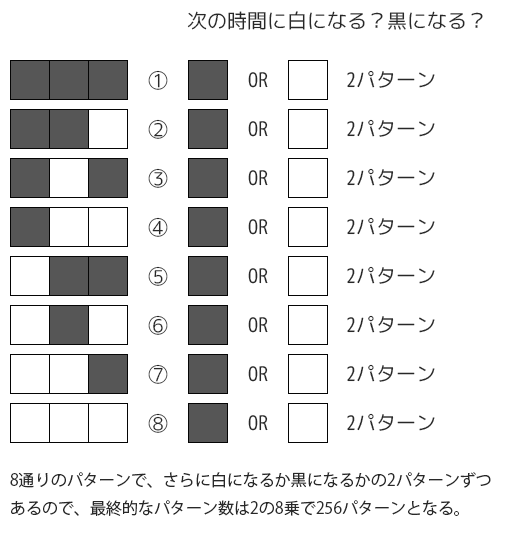
8個のパターンで、次の時間にそれぞれ黒か白（1か0）のどちらになるので、256パターンある

前述の8つのパターンで、それぞれ次の時間が黒になるのか白になるのかのパターン数を調べると、$2^8 = 256$パターン存在します。

201908016_1.png

1次元のセルラー・オートマトンを体系的に研究したスティーブン・ウルフラムさん（1980年ごろ）によると、この256パターンを、0～255の範囲で「ルール0」～「ルール255」と呼ぶそうです。（30番目のルールであれば「ルール29」といった具合に）

この各ルールで、生成される模様が異なったり、傾向によってクラスターが分けられたりしています。

Pythonで動かしてみる

以下のようなものをPythonで書いて作ってみます。

  • 1行ずつ更新がされる。
  • 最初は全て0で初期化し、その後に1番上の行の真ん中のみ1にする（その1の部分をトリガーにその後の反応が起きるようにする）。
  • 各行で、現在の値に応じて次の時間が0か1かに変化するようにします。

使う環境

ビットシフトを思い出す＆調べる

別の言語ではビットシフトなどを昔使っていた時期もありますが、長いこと使わない生活をしていたのと、Pythonでは使ったことがないため、調べつつ復習しておきます（今回、各ルールを反映するために使用します）。

参考 : Python ビット演算 超入門

今回使うのは、前述の8パターンでそれぞれが0になるのか1になるのかという値です。

たとえば、00001111といったような値になります。

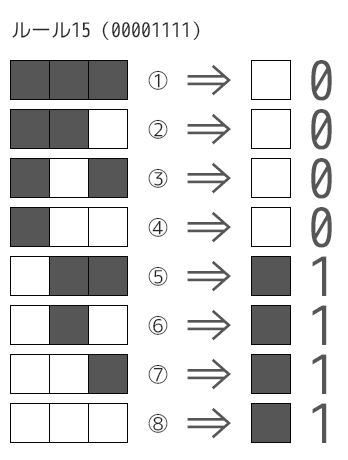
どうやらPythonでは先頭に0bと付けることで、2進数で表現することができるようです。先ほどの00001111を例に挙げると、15になります。

0b00001111

15

これがウルフラムさんの研究で言うところのルール15になります。

20190816_2.png

※2進数で、1111と表現しても同様に15になりますが、今回は8パターンに合わせて8つの数値で00001111といったように表現します。

0b1111

15

00000000で0、00000001で1、0b00000010で2、0b00000011で3...と増えていきます。

0b00000000

0

0b00000001

1

0b00000010

2

0b00000011

3

最後となるルール255は、8つの数字が全て1のケースとなります。

0b11111111

255

また、10進数などを2進数にしたい場合には、binでキャストすると変換してくれます。

bin(15)

'0b1111'

2進数の数値を左にずらす（ビットシフトの左シフト）処理は、Pythonでは元の数字 << ずらす桁数と書くと表現できます。
以下のように1 << 0とすると、1が左に0動く（0なので値そのまま）となります。

bin(1 << 0)

'0b1'

1 << 1とすると、1が左に1桁分移動するので、0b10になります。 同様に、1 << 2とすれば2桁分移動して0b100となります。

bin(1 << 1)

'0b10'

bin(1 << 2)

'0b100'

右方向に移動させる右シフトは、逆に>>の記号を使って表現します。

bin(15 >> 0)

'0b1111'

bin(15 >> 1)

'0b111'

ルール番号に応じた、次の時間の値を求めるには？

現在の3つの値（左・中央・右）の値（0か1か）と、算出したいルール（例えばルール15であれば00001111）を求めるにはどうすればいいのでしょうか？

まずは3つの値から、0～7までの番号を算出するコードを考えます。
left、center、rightという三つの変数を用意し、それぞれが0か1を取るようにします。

left = 0
center = 0
right = 0

これらの変数を、8パターンを表現するには$2^3$が必要なので、2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * rightという計算をすると、0～7までの8パターンが表現できます（2進数で表すと0b000～0b111までが表現できます）。

left = 0
center = 0
right = 0

2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right

0

left = 0
center = 0
right = 1

2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right

1

left = 0
center = 1
right = 0

2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right

2

...

left = 1
center = 1
right = 1

2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right

7

ルール1であれば0b00000001となり、ルール15であれば0b00001111、ルール16であれば0b00010000となります。算出するにはこれらの値を右端（1桁目）から見ていって、対象の値が0なのか1なのかを確認すればいいことが分かります。
つまり、前述の0～7までの値分を右シフトして、残った値の1桁目が0なのか1なのかで判定すれば求めることができます。
ルール1であれば0で右シフトすれば1、1～7で右シフトすれば0となり、ルール15であれば0～3で右シフトすれば1、4～7で右シフトすれば0となり、ルール16であれば4で右シフトした時のみ1、それ以外は0となるといった具合です。

1桁目の値が0なのか1なのかの算出に、論理積を使います。右辺の値を1桁の1で設定すれば、左辺も1桁目の値が参照されて0か1かの算出がされます。
1桁目のみで計算されるので、掛け算と同じような挙動になります。左辺と右辺が両方1になるなる時のみ結果が1となり、それ以外のバターンは全て0になります。

両辺とも0のケース :

0b0 & 0b0

0

左辺のみ1のケース :

0b1 & 0b0

0

右辺のみ1のケース :

0b0 & 0b1

0

両辺とも1のケース :

0b1 & 0b1

1

左辺の1桁目が0の場合（10） :

0b10 & 0b1

0

左辺の1桁目が1の場合（11） :

0b11 & 0b1

1

前述の左中央右の0と1の値から8パターンを算出する計算と、論理積で期待していた結果が得られます。
たとえば、ルール15（0b00001111）であれば、0～3が1、4～7が0となる結果が得られます。

(15 >> 0) & 1

1

(15 >> 1) & 1

1

(15 >> 2) & 1

1

(15 >> 3) & 1

(15 >> 4) & 1

0

...

(15 >> 7) & 1

0

他の、たとえばルール16（0b00010000）でも試してみましょう。4桁分右シフトした時のみ1となり、他は0になります。

(16 >> 4) & 1

1

(16 >> 0) & 1

0

(16 >> 7) & 1

0

この辺りは、（書籍のコードを初見で見た時に）非理系出身の身からすると少し頭が混乱しますね・・・
（自分で整理すると理解できる・・）

これで必要なビットシフトの復習や調査ができたので、コードの内容に本格的に入っていきます。

実装を進める

一部、可視化用に利用するため、githubのリポジトリをクローンしておきます。alifebook_libパッケージ以下を利用します。

まずは必要なモジュールのimportと可視化用のオブジェクトを用意しておきます。

import numpy as np

from alifebook_lib.visualizers import ArrayVisualizer

visualizer = ArrayVisualizer()

可視化用のウインドウが立ち上がります。

20190817_1.png

続いて可視化領域のサイズを指定します。今回は600x600ピクセルの領域に描画していきます。

SPACE_SIZE = 600

試すルール番号を定義します。今回はルール30を使います。

RULE = 30

セルラー・オートマトンの状態のベクトルを初期化します。現在の状態と、次の状態を保持する必要があるので、それぞれstateとnext_stateという名前で扱います。
サイズは、可視化領域の1行分を扱うので、SPACE_SIZEの600のベクトルとなります。

state = np.zeros(shape=SPACE_SIZE, dtype=np.int8)
next_state = np.zeros(shape=SPACE_SIZE, dtype=np.int8)

このままだと全て値が0ですが、初期値として最初の状態の真ん中のみ1に調整します。こうすることで、一番上の真ん中部分から反応が生まれてきます。

state[len(state) // 2] = 1

続いて、現在の状態が次の時間にどのような状態になるのかの計算をループで実行します。
ビットシフト関係の節で触れたように、左・中央・右の値を取得します。

while True:
    for i in range(SPACE_SIZE):
        left = state[i - 1]
        center = state[i]
        right = state[(i + 1) % SPACE_SIZE]

中央のインデックスが0の時、左のインデックスは-1となりますが、-1のインデックスは最後のインデックスが参照される（今回はベクトルの右端の数値が参照される）ため問題ありません。

右の方は、中央のインデックスが右端の場合（599）にそのままだと600でインデックスを超えてしまうので、剰余を求めることで、そういったケースには左端になるようにしてあります。

続いて、前述のビットシフトなどの節の計算を使って、0～7のパターンのインデックスを算出する計算と、右シフトと論理積で次の時間の状態を算出・設定する処理を追加します。

        pattern_index = 2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right
        
        next_state[i] = RULE >> pattern_index & 1

そして、1行分の計算（SPACE_SIZE件数分のループ）が1回終わったら、次の時間の状態の計算結果を現在の状態のベクトルに持ってきて、可視化の状態を更新して終わりです。

    state[:] = next_state[:]
    visualizer.update(1 - state)

色は0が黒、1が白ですが、今回は逆（1が黒）で扱うので、1 - stateとして0が1、1が0になるようにしてあります。

コード全体

import numpy as np

from alifebook_lib.visualizers import ArrayVisualizer

visualizer = ArrayVisualizer()

SPACE_SIZE = 600
RULE = 30

state = np.zeros(shape=SPACE_SIZE, dtype=np.int8)
next_state = np.zeros(shape=SPACE_SIZE, dtype=np.int8)
state[len(state) // 2] = 1

while True:
    for i in range(SPACE_SIZE):
        left = state[i - 1]
        center = state[i]
        right = state[(i + 1) % SPACE_SIZE]
        
        pattern_index = 2 ** 2 * left + 2 ** 1 * center + 2 ** 0 * right
        
        next_state[i] = RULE >> pattern_index & 1
    
    state[:] = next_state[:]
    visualizer.update(1 - state)

完成です！
実行してみると、wikipediaのページのサンプルにあるような、以下のような模様が生成されます。

20190817_2 102.png

アニメーションで見てみると、初期値の真っ黒な状態から、while文のループで次の状態が更新され続け、且つ可視化のモジュールで1回更新するたびに更新箇所が1行下がるので、段々上から模様が生成されていることが分かります（縮小したので小さくて潰れていますが・・・）。

20190817_3.gif

参考文献まとめ

15
7
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
15
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?