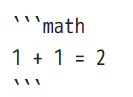Qiitaなどに数式のメモを取ったり写経したりする際に、よく忘れるのでメモ。(この記号LaTeXだとどう書くんだっけ・・といった具合に)
理系出身ではないため、間違っている点、改善した方がいい点などは、弱めにマサカリ投げていただけますと幸いです。
※重いのでデスクトップなどでの閲覧をお勧めします。(数式表示まで恐らく少しかかります)
※Chrome以外では表示が崩れているかもしれません。記事閲覧の際にはChrome推奨です。
Qiita上でLaTeXを使う際には
1 + 1 = 2
もしくは文章中(インライン)で差し込みたい場合には、$記号で囲みます。$A^2$といった感じに文章中に記載すると、$A^2$のように表示されます。
下付き文字などは、時々インラインでうまく認識してくれない時があるので、記号の前に\のエスケープ記号を置いたりします。$A\_2$といった具合です。
ガンマ記号
ハイパーパラメーターなどで出てきます。\gammaと記載します。
\textrm{exp}
(- \gamma || x - \ell ||^2)
\textrm{exp}
(- \gamma || x - \ell ||^2)
大文字の方も、ガンマ分布関係のガンマ関数云々で出てきたりします。
\Gammaと記載します。
\frac
{β^α x^{α - 1}e^{-βx}}
{\Gamma (α)}
エル(リットルの)記号
そのまま、ℓと記述してもいいですが、コマンドで記述する際には\ellと記載します。サンプルは前述したガンマ記号の個所をご確認ください。
エプシロン記号
こちらも、ハイパーパラメーターなどで使われます。(Scikit-LearnのSVMでは、道幅的なパラメーターに、LinearSVR(epsilon=1.5)といった具合で使われたり等)
\epsilonと書くと、$\epsilon$といったように表示されます。
ゼータ記号
そのままζと書いてもいいですが、コマンドで書く際には\zetaと書くと$\zeta$となります。
ミュー記号
平均などを表すために使われたりします。(meanのmに由来するのでしょうか?)
ミューと入力して直接μと書くか、コマンドでは\muと書くと$\mu$と表示されます。
シグマ記号
色々使われますが、例えば標準偏差(standard deviation)であったり、シグモイド関数を表す際などに使われます。σと直接書くか、コマンドの場合は\sigmaと書くと$\sigma$と表示されます。
ニュー記号
νと直接書くか、\nuとコマンドでは書くと$\nu$となります。
ラムダ記号
直接λと記載するか、\lambdaと記載すると$\lambda$と表示されます。
タウ記号
直接τと記載するか、\tauと記載すると$\tau$と表示されます。
時系列関係なんかで見たりします。
オメガ記号
小文字の場合は\omega、大文字の場合は\Omegaと記述すると、それぞれ$\omega$、$\Omega$となります。
E[R_T] =
\Omega (\textrm{log}(T))
E[R_T] =
\Omega (\textrm{log}(T))
ファイ記号
直接Φと書くか、コマンドで\phiとすると$\phi$と表示されます。
デルタ記号
δと直接書くか、コマンドで\deltaと書くと$\delta$と表示されます。大文字で\Deltaと書くと、$\Delta$となり、\nablaの逆のような記号になります。
varが付く、似た記号
書籍で出てきた際など、varが付かないものと似ていて結構混乱します。且つ、よく忘れます。意味合い的には、varが付かない記号と近い用途で使われたり、ケースバイケースな感じでしょうか?(参考 : \varepsilon vs. \epsilon)
- \varepsilon : $\varepsilon$
- \vartheta : $\vartheta$
- \varpi : $\varpi$
- \varsigma : $\varsigma$
- \varphi : $\varphi$
上付き文字
^ 記号を使います。1文字を超える場合には、{}で囲みます。
x^{(1)}
x^{(1)}
下付き文字
_ 記号を使います。上付き文字同様、1文字を超える場合には{}で囲みます。
n_{p - 1}
n_{p - 1}
分数
\frac{分子}{分母} と記載します。(分数 = fraction)
\frac{1}{m}
\frac{1}{m}
平方根
\sqrt{内容}と記載します。(平方根 = square root)
\sqrt{2}
\sqrt{2}
総和
for文の記述と、内容をすべてプラスしていくイメージ。
\sum_{下限}^{上限}のフォーマットで記載します。
\sum^m_{i = 1}
(h(x^{(i)}) - y^{(i)})^2
\sum^m_{i = 1}
(h(x^{(i)}) - y^{(i)})^2
総乗
for文の記述と、内容をすべて乗算していくイメージ。
総和と大体記述方法は同じで、\sumの代わりに\prod_{下限}^{上限}と記述します。(product)
1文字だけの場合には{}の括弧は省略可です。
\prod_{i = 0}^{n}
x_i
\prod_{i = 0}^{n}
x_i
改行
通常の改行だと改行してくれないので、\\といったように、エスケープ記号を二つ並べます。
100\\
200
100\\
200
スペースを入れる
LaTeXだと、通常はスペースや改行を入れても無視されますが、レイアウト的にスペースを入れたい場合にはエスケープとスペースで\ といったように記述します。
通常は スペースが無視されます。
通常は スペースが無視されます。
スペースを入れたい場合には、\ \ \ \ \ エスケープとスペースを入れます。
スペースを入れたい場合には、\ \ \ \ \ エスケープとスペースを入れます。
ベクトル / 行列の書き方
複数の要素を並べたりしたい場合には、\begin{array}{c}内容\end{array}といった書き方をします。例えば100と200の2つの要素を縦に並べる場合は、
\begin{array}{c}
100\\
200
\end{array}
\begin{array}{c}
100\\
200
\end{array}
といった記述になります。
cの部分は、整列設定(左揃えなのか、中央揃えなのかetc)となり、lが左揃え(left)、cが中央揃え(center)、rが右揃え(right)になります。
複数記述することで、必要な列数を定義します。3列であれば、cccといった具合です。
列の区切りは&で記述します。
\begin{array}{ccc}
100 & 200 & 300\\
400 & 500 & 600
\end{array}
\begin{array}{ccc}
100 & 200 & 300\\
400 & 500 & 600
\end{array}
最後に、左右の括弧を記述して完了です。括弧は、beginとendの外側に、\left( 内容 \right) といったように記述します。leftやrightの後の部分には必要な(や{などの記号を配置します。
Qiitaで{を指定する際には、エスケープを置いて\{といった具合に記述します。
\left(
\begin{array}{ccc}
100 & 200 & 300\\
400 & 500 & 600
\end{array}
\right)
\left\{
\begin{array}{ccc}
100 & 200 & 300\\
400 & 500 & 600
\end{array}
\right\}
縦の三点リーダ
ベクトル / 行列内などでよく見かけます。
\vdots と記載します。
\left(
\begin{array}{c}
(x^{(1)})^T\\
\vdots\\
(x^{(1000)})^T\\
\end{array}
\right)
\left(
\begin{array}{c}
(x^{(1)})^T\\
\vdots\\
(x^{(1000)})^T\\
\end{array}
\right)
要素の上に^記号
\hat{要素}と記載します。
\hat{y}^{(i)} = h(x^{(i)})
\hat{y}^{(i)} = h(x^{(i)})
たとえばyに近い要素だけど、ちょっとyとは違うもの、といったものに使われたりするようです。($y$は出力値、$\hat{y}$は推論値といった具合に)
要素の上にドット記号
こちらも、^記号に近いですが、対象の要素に近いけど、少し条件が付く、といった場合などに使われるようです。\dot{要素}と書きます。
\dot{x}^{(i)}
\dot{x}^{(i)}
要素の上に横線
\overline{要素}と記載します。
\overline{R}_T =
E[R_T]
\overline{R}_T =
E[R_T]
要素の上に波線
\tilde{要素}とすると、$\tilde{a}$といった表示になります。要素が複数文字で長い場合などには、\widetildeと記載すると、$\widetilde{ab}$といった具合に長くなります。
要素の上に矢印
右向きの場合には、\overrightarrow{要素}、左向きの場合には\overleftarrow{要素}と記述します。
伝播方向の表現などで使われているようです。
\overrightarrow{h}(t)
\overrightarrow{h}(t)
\overleftarrow{h}(t)
\overleftarrow{h}(t)
ローマン体でのテキストの記述
場合によっては、デフォルトのフォントよりも、ローマン体などの方が読みやすかったり、書籍での表示に近いものになるケースもあります。
たとえば、$precision$よりも$\textrm{precision}$の方が読みやすいよね、といった具合です。
\textrm{内容}と記載します。通常LaTeXではスペースなどは無視されますが、\textrm内の内容部分ではスペースなどが効くようになります。
また、内部に他のLaTeXコマンドの記述をしても反映されません。
2 × \frac
{\textrm{precision} × \textrm{recall}}
{\textrm{precision} + \textrm{recall}}
2 × \frac
{\textrm{precision} × \textrm{recall}}
{\textrm{precision} + \textrm{recall}}
偏微分記号
勾配云々の話で出てきます。
\partialと記述します。(偏微分=partial derivative)
\frac
{\partial}
{\partial θ_j}
\frac
{\partial}
{\partial θ_j}
逆三角形記号
こちらも勾配云々の話で出てきたりします。\nablaと記載します。
\nabla_θ \textrm{MSE}(θ)
\nabla_θ \textrm{MSE}(θ)
学習率記号
学習率などでの小さな値の$\eta$記号は、\etaと記述します。
語源的に縮小辞云々のものに由来して、小さい値に使われるのでしょうか?よく把握していません。
指小辞の場合は、「小さい」「親近感がある」「かわいい」などのような意味を本来の言葉に加える働きがあります。
...
–ete/-eta
この指小辞は、カタルーニャ語、やバレンシア語、アラゴン語など、まだスペインで話され続けている言語から来たと考えられています。
スペイン語でよく使われる指小辞、-ito,-itaとは?
\eta \nabla_θMSE(θ)
\eta \nabla_θMSE(θ)
※コメントでご指摘いただきました!ありがとうございますmm
いえ, この\etaはギリシア文字のエータ(Η, η)を意味します。
普通のギリシア文字なので, 特別な記号というわけではないです。
左側のみ括弧を記述したい
\left、\rightで括弧を記述する際に、\rightの方を省略するとエラーになってしまいます。
そのため、右側の括弧を省略したい場合にはドットを記載し、\right.といったように書きます。
\left\{
\begin{array}{lll}
-1 & \textrm{if} & θ_i < 0\\
0 & \textrm{if} & θ_i = 0\\
+1 & \textrm{if} & θ_i > 0
\end{array}
\right.
\left\{
\begin{array}{lll}
-1 & \textrm{if} & θ_i < 0\\
0 & \textrm{if} & θ_i = 0\\
+1 & \textrm{if} & θ_i > 0
\end{array}
\right.
要素の下に小さな要素を配置したい
\underset{下の要素}{上の要素}と記載します。
\underset{k}{\textrm{argmax}}
\underset{k}{\textrm{argmax}}
近似記号
\approxと記載します。(近似 = approximation)
\textrm{exp}
(-0.3 × 1^2)
\approx 0.30
\textrm{exp}
(-0.3 × 1^2)
\approx 0.30
~記号が使われることもあるようです。コマンドでは\simと記載します。
(similarに由来すると思われます。)
なお、この記号は他にも色々使われたりするそうですが、確率などの方面では、$X \sim 〇〇$といった書き方が出てきた場合は、Xは〇〇の分布、といった扱いになることが多いようです。参考 : What does ∼ mean in math and statistics?
\underset
{x \sim P_{\textrm{data}}(x)}
{\mathbb{E}}
\underset
{x \sim P_{\textrm{data}}(x)}
{\mathbb{E}}
比例記号
AはBに比例する、という意味の記号の$\propto$には、\proptoと記述します。proportional(=比例した)に由来します。
\frac
{P(X|A)P(A)}
{P(X)}
\propto
P(X|A)P(A)
\frac
{P(X|A)P(A)}
{P(X)}
\propto
P(X|A)P(A)
定義
AをBとして定義する、といった際には:=記号を使います。
p := Wx + b
要素ごとの乗算 / 除算
行列などでの要素ごと(element-wise)の乗算(アダマール積 / Hadamard product)は、\otimesと書き、除算は\oslashと書きます。(それぞれ、$\otimes$、$\oslash$となります)
それぞれ〇としてo、それに加えて掛け算なのでtimes、除算なのでslashという意味に捉えると覚えやすいかもしれません?
書籍によっては乗算のものは、\circで$\circ$が使われたり、\odotで$\odot$などが使われたりします。
中抜き文字
\mathbb{内容}と記載します。bbは、黒板ボールド(中抜き文字, blackboard bold)に由来します。
V(s) = \mathbb{E}[G|S_t = s]
V(s) = \mathbb{E}[G|S_t = s]
集合
直接∈と記載するか、コマンドでは\inと記載すると$\in$という表示になります。逆向きの記号は\niと記載します($\ni$)。inの逆だからniといった具合でしょうか。
否定は\notinと記載します($\notin$)。
\eta \in \{1, 2\}
\eta \in \{1, 2\}
カリグラフィー文字
$\mathcal{L}$、$\mathcal{Z}$、$\mathcal{S}$といった文字を表示する際には、\mathcal{記号}と記載します。(calはcalligraphicに由来します)
\mathcal{L}_D =
\mathcal{L}(x) - k_t \mathcal{L}(G(z_D))
\ \ \ \textrm{for}\ θ_D
\mathcal{L}_D =
\mathcal{L}(x) - k_t \mathcal{L}(G(z_D))
\ \ \ \textrm{for}\ θ_D
数式番号の表示
右端に数式番号などを表示したい場合には、\tag{番号}と記載します。たとえば、第5章での8番目の数式として表したい場合に、以下のように記述します。
\tag{5.8}
h_(1) = \sigma (W_x + b)
\tag{5.8}
h_(1) = \sigma (W_x + b)
要素を境界線で囲む
\fbox{要素}と記載します。なお、この括弧内の要素では各コマンドなどが使われず、そのまま表示されます。$\fbox{A_1}$といったように、下付き文字などを指定してもそのままの文字で表示されます。
コマンドを使いたい場合は、下記のように括弧内でさらに要素を$記号で囲みます。
\fbox{$f(1) ... f{(\tau)}$}
\fbox{$f(1) ... f{(\tau)}$}
数式参考
- Hands-On Machine Learning with Scikit-Learn and TensorFlow
- Deep Learning (Adaptive Computation and Machine Learning)
- Deep Reinforcement Learning Hands-On
- Pythonで体験するベイズ推論
- Learning Generative Adversarial Networks
- 詳解 ディープラーニング
他の既読本も振り返ろうと思ったけど、力尽きたよ!
おまけ
Jupyter上では、SymPyなども併用すると幸せになれるかもしれない・・