TL;DR
ALife(人工生命)の分野で出てきた、自然界にあるようなパターン(模様)もしくは微生物の細胞分裂のような動きが作られていく「自己組織化」なるものを、Gray-Scottと呼ばれるモデルを使ってPythonで計算してアニメーションさせて遊びます。以下の画像みたいなアニメーションです。
主な参考文献
また、上記書籍のgithubのリポジトリのコードもMITライセンスなので参照・利用させていただきますmm
※本記事では割愛した説明なども山ほどあるので、ALife関係の詳細は書籍をお買い求めください。
自己組織化とは
きっちりと設計図を用意しなくても、時間経過とともに与えられた条件に応じて構造が決まっていくことを言うそうです。
(なんとなくルールベース ⇔ 強化学習的な関係に近いと思いました)
今回は自己組織化を踏まえつつ、自然界にあるようなパターンが時間経過と共に形成されていくものを作ります(たとえば、自然界のひび割れの模様や、深海魚の模様に近いものを)。
Gray-Scottモデルとは
科学者のGrayさんとScottさんが1983年に発表した論文に名前は由来するようです。
対象論文 : Autocatalytic reactions in the isothermal, continuous stirred tank reactor: Isolas and other forms of multistability
反応拡散系というモデルの一つに該当します。
反応拡散系(はんのうかくさんけい、英: reaction-diffusion system)とは、空間に分布された一種あるいは複数種の物質の濃度が、物質がお互いに変化し合うような局所的な化学反応と、空間全体に物質が広がる拡散の、二つのプロセスの影響によって変化する様子を数理モデル化したものである。
反応拡散系 - Wikipedia より。
2つの物質UとV(式などは後述)がお互いに「反応」し、また時間経過として拡散していく形で表現されます。
Gray-Scottモデルの反応の流れと式
- 物質Uが一定の補充率(feed rate)で追加されます。
- 2つのVがUを一つ消化して、3つのVに変化(反応)します。式で表すと以下のようになります。
U + 2V → 3V
- 物質Vは一定の減量率(kill rate)で取り除かれます。取り除かれた状態をP(これ以上反応しないので、不活性物質と呼ばれます)とすると、式は以下のようになります。
V → P
バクテリアVが餌Uを食べながら増殖していく過程を想像するとわかりやすいかもしれません.
Turingパターンでメリークリスマス
Uが食べられて、Vが増えていくという感じですかね。以下の実際のUの濃度を可視化のアニメーションでも、増殖するようなイメージで広がっていっているのが分かります(以降Uの濃度をu、Vの濃度をvと表記します)。

Uの濃度uとVの濃度vの増減量の式
時間経過によるUの濃度uの増減量($\frac{\partial u}{\partial t}$)とVの濃度vの増減量($\frac{\partial v}{\partial t}$)は以下の式で表されます。
\tag{1}
\frac{\partial u}{\partial t}
= Du \Delta u - uv^2 + f(1 - u)
\tag{2}
\frac{\partial v}{\partial t}
= Dv \Delta v + uv^2 - v(f + k)
それぞれの式は「拡散(Diffusion)」部分と「反応(Reaction)」部分と「流入(Inflow)(式(1))」もしくは「流出(Outflow)(式(2))」の3つの項から構成されています。
- $Du$と$Dv$は拡散定数と呼ばれる値で、濃度uとvがそれぞれどのくらいの速さで拡散するのかの一定の値です。基本的にuの方が早く拡散するように、$Du$のほうが大きい値が設定されます。
- $\Delta u$と$\Delta v$は、濃度uとvの各地点における周辺との濃度差を無くすための表現で、ラプラシアンと呼ばれるようです。濃度が濃い箇所は薄くなるように周辺に拡散し、逆に薄い箇所には周囲から流入する形となります。可視化のアニメーションを見ても、段々と濃度が薄い(白い領域)に全体的にバランスよく拡散していくのが分かります。

一言で言うと, その物質の濃度の差が無くなる方向に拡散するときの強さのようなものです.
ちなみに, 熱伝導方程式も同じ形で書けます.
Turingパターンでメリークリスマス
- 前述の$Du \Delta u$と$Dv \Delta v$の部分が、「拡散(Diffusion)」の項に該当します。
- $- uv^2$と$+ uv^2$の部分は反応速度の項となります。
- $U + 2V → 3V$の物質の反応の式における、Vの生成速度を$uv^2$という式が表し、それぞれ式(1)と式(2)でプラスマイナスの符号が異なるのはUがVに変化することによって濃度uが減る(式(1))のとvが増える(式(2)) という点を表現しています。
- 式(1)の$+ f(1 - u)$は物質Uの流入(Inflow)による補充(feed)を表します。
- 濃度uが低いほどUの流入は多くなり、逆に濃度が濃いほど流入は少なくなります。最大濃度1になった時点で流入が止まります。
- 式(2)の$- v(f + k)$は流出(Outflow)による減量(kill)を表します。
- 濃度vが高いほどたくさん流出し、vが0になると流出が止まります。
これらの計算によって、「反応してVが増えて」「Uが減り」、そして「Uが減ることによって濃度が低くなるのでUが流入し」、「ラプラシアンによって周囲とバランスが取られ」、「拡散によって中央から段々広がっていく」という、前述の可視化の画像のようなアニメーションになります。
Pythonで実装してみる
非理系のエンジニアの身からすると、数式よりもプログラムを書いていたほうが理解ができるので、実装していきす。
なお、行列の可視化(前述のアニメーション画像など)はgithubにあるMatrixVisualizerを使わせていただきます(後述するfrom alifebook_lib.visualizers部分)。
また、書籍のコードで言うとgray_scott.pyが該当します。
使った環境
- Windows
- Python 3.6.8 :: Anaconda, Inc.
- NumPy==1.14.5
- Vispy==0.5.3
- 前述の書籍のgithubのコード
- Jupyter notebook
まずは初期化する
githubのコードを落としてきた(importができる)状態で、進めていきます。
import os
import sys
import numpy as np
from alifebook_lib.visualizers import MatrixVisualizer
MatrixVisualizerは前述した通り、行列のアニメーションの可視化として利用します。
以下のように初期化すると、可視化用に新しいウインドウが起動します(初期表示では真っ白です)。
続いて、グリッド数(実質行列のサイズ)のSPACE_GRID_SIZE、シミュレーションする1つ辺りの空間サイズのパラメーターのdx、シミュレーションで何ステップごとに表示を更新するのかのVISUALIZATION_STEPを定義します。
SPACE_GRID_SIZEはピクセル的なところ、VISUALIZATION_STEPはフレームレート的なところに絡んできます。基本的にこの辺りは変えなくて良さそうなのでこの値のまま進めていきます。
続いて濃度uとvの拡散係数の定数である$Du$や$Dv$を定義します。前述の通り、uの拡散係数のほうが大きいほうが好ましいそうなのでそちらを大きくします。
SPACE_GRID_SIZE = 256
VISUALIZATION_STEP = 8
dx = 0.01
Du = 2e-5
Dv = 1e-5
次は補充(feed)のパラメーターであるfと減量(kill)のパラメーターのkを定義します。
これらはハイパーパラメーターのようなもので、うまいこと設定すると良い感じのアニメーションになりますし、組み合わせによっては微妙なアニメーションになります。この値の組み合わせ次第でアニメーションが大きく変わってきます。
今回は以下の模様の生成結果になる組み合わせでfとkを設定します。

f = 0.022
k = 0.051
※他にも、うまいことアニメーションしてくれる値の組み合わせの一例として、f=0.04, k=0.06とかf=0.035, k=0.065とか、f=0.012, k=0.05とかがあるようです。
次は濃度のuとvを初期化します。NumPyでuを1(ones)で埋めて、vを0(zeros)で埋めます。
行列サイズは事前に定義したSPACE_GRID_SIZE(実質ピクセル数的な値)を設定します。
u = np.ones(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
v = np.zeros(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
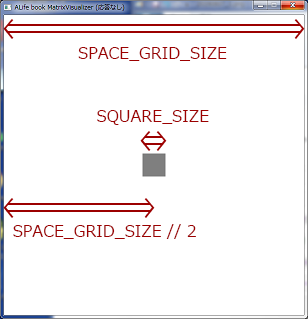
これだけだと反応が起きてくれないので、uとvの行列の真ん中に正方形を描きます。こうすることで、真ん中から反応が始まり、拡散によって周囲に広がっていきます。
四角の一辺のサイズはSQUARE_SIZEとして定義します。uとvで対象の四角をそれぞれ0.5と0.25のグレーで埋めます(0が黒、1が白の領域になります)。
square_start = SPACE_GRID_SIZE // 2 - SQUARE_SIZE // 2
square_end = SPACE_GRID_SIZE // 2 + SQUARE_SIZE // 2
u[square_start:square_end, square_start:square_end] = 0.5
v[square_start:square_end, square_start:square_end] = 0.25
visualizerのupdateメソッドで行列を指定すると、その行列の内容を確認できます。uとvの表示を確認してみましょう。
visualizer.update(matrix=u)
白い領域(ones)にグレーの正方形がSQUARE_SIZEのサイズで中央にあるのが分かります。
visualizer.update(matrix=v)
vの方は黒い領域(zeros)にグレーの正方形があるのが分かります。
各計算を図で表すと以下のようになります。
ラプラシアンの計算
続いてラプラシアンの計算の実装です。
そもそもラプラシアンってなんだ・・・という感じですが、Wikipediaによると、
数学におけるラプラス作用素(ラプラスさようそ、英: Laplace operator)あるいはラプラシアン(英: Laplacian)は、ユークリッド空間上の函数の勾配の発散として与えられる微分作用素である。
ラプラス作用素 - Wikipedia
とのことです。いまいちピンと来ませんが、温度が低いところと高いところで混ざっていく(冷水が段々温くなる的な)とか、今回みたいな濃度の高い領域から低いところに拡散していくような計算、ということで考えることにしました(数学者ではないので厳密な理解は出来ていなくてもとりあえずはいいでしょうということで・・)。
周辺へ流入したり、逆に流出したりをNumPyで書く必要がありますが、それにはroll関数を使います。roll関数を知らず、初見の際に「rolling的に移動平均関係か?」と思いましたが、そんなことはなく行列を特定の軸方向に対して回転させる計算となります。
3x3小さい行列でroll関数を少し試してみましょう。
arr = np.arange(0, 9)
arr = arr.reshape((3, 3))
arr
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
roll関数には、a引数に行列、shift引数に回転量、axis引数に行方向もしくは列方向を指定します。
たとえば、axis=0, shift=1と設定すれば下方向に値がスライドします。末端の位置にあった値は一番上に戻ってきます。
# 行列の値が ↓ ↓ ↓ という方向に移動する。
np.roll(a=arr, shift=1, axis=0)
array([[6, 7, 8],
[0, 1, 2],
[3, 4, 5]])
shiftで-1などの負の値を設定すれば、逆の方向に移動します。たとえば、axis=0, shift=-1と指定すれば、上方向に行列の値が移動します。
# 行列の値が ↑↑↑ という方向に移動する。
np.roll(a=arr, shift=-1, axis=0)
array([[3, 4, 5],
[6, 7, 8],
[0, 1, 2]])
axisが1のときは列方向に移動するだけで内容は一緒です。shiftが正なら右方向、負なら左方向に値が動きます。
np.roll(a=arr, shift=1, axis=1)
array([[2, 0, 1],
[5, 3, 4],
[8, 6, 7]])
よって、濃度uの流入量(Inflow)の各方向からの各値のラプラシアンの値の計算は以下のようになります。
u_inflow_from_top = np.roll(a=u, shift=1, axis=0)
u_inflow_from_bottom = np.roll(a=u, shift=-1, axis=0)
u_inflow_from_left = np.roll(a=u, shift=1, axis=1)
u_inflow_from_right = np.roll(a=u, shift=-1, axis=1)
そして、流入とは逆に四方向に流出(Outflow)していく計算も必要になりますが、そちらは- 4 * uという計算になります。
u_outflow = 4 * u
最後に、一度に空間サイズのパラメーター(どのくらい大きいサイズでシミュレーションするかの値)であるdxの2乗で除算する/ (dx * dx)でラプラシアンの計算は完成です(空間のサイズによって、物質の移動量の総和が変わるので計算上必要になります)。
上記を踏まえ、ラプラシアンの値は以下のようになります。
laplacian_u = (u_inflow_from_top + u_inflow_from_bottom
+ u_inflow_from_left + u_inflow_from_right
- u_outflow) / (dx * dx)
vもuと同様の計算になります。
v_inflow_from_top = np.roll(a=v, shift=1, axis=0)
v_inflow_from_bottom = np.roll(a=v, shift=-1, axis=0)
v_inflow_from_left = np.roll(a=v, shift=1, axis=1)
v_inflow_from_right = np.roll(a=v, shift=-1, axis=1)
v_outflow = 4 * v
laplacian_v = (v_inflow_from_top + v_inflow_from_bottom
+ v_inflow_from_left + v_inflow_from_right
- v_outflow) / (dx * dx)
拡散の計算
ラプラシアンの計算が書けたので、拡散部分の計算に移ります。式(1)と式(2)でいうと、$Du\Delta u$と$Dv\Delta v$の箇所です。$\Delta u$と$\Delta v$はラプラシアンの値なので既に計算済みです。また、$Du$と$Dv$は拡散関係の定数値なので、単純に定数とラプラシアンを乗算するだけです。計算された増減量をuとvに加えていきます。
du_lap = Du * laplacian_u
dv_lap = Dv * laplacian_v
u += du_lap
v += dv_lap
これで拡散の計算は終わりですが、この計算を拡散中は繰り返し実行する(ステップを繰り返す)必要があるので、while文を設定し、さらに一度に更新する量の定義であるVISUALIZATION_STEP回数分更新を一度に実行します。
(VISUALIZATION_STEP回数分拡散の更新がされたら、visualizerの可視化の内容も更新しています)
# 濃度uとvの初期化処理。
u = np.ones(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
v = np.zeros(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
square_start = SPACE_GRID_SIZE // 2 - SQUARE_SIZE // 2
square_end = SPACE_GRID_SIZE // 2 + SQUARE_SIZE // 2
u[square_start:square_end, square_start:square_end] = 0.5
v[square_start:square_end, square_start:square_end] = 0.25
while True:
for i in range(VISUALIZATION_STEP):
# uのラプラシアンの算出。
u_inflow_from_top = np.roll(a=u, shift=1, axis=0)
u_inflow_from_bottom = np.roll(a=u, shift=-1, axis=0)
u_inflow_from_left = np.roll(a=u, shift=1, axis=1)
u_inflow_from_right = np.roll(a=u, shift=-1, axis=1)
u_outflow = 4 * u
laplacian_u = (u_inflow_from_top + u_inflow_from_bottom
+ u_inflow_from_left + u_inflow_from_right
- u_outflow) / (dx * dx)
# vのラプラシアンの算出。
v_inflow_from_top = np.roll(a=v, shift=1, axis=0)
v_inflow_from_bottom = np.roll(a=v, shift=-1, axis=0)
v_inflow_from_left = np.roll(a=v, shift=1, axis=1)
v_inflow_from_right = np.roll(a=v, shift=-1, axis=1)
v_outflow = 4 * v
laplacian_v = (v_inflow_from_top + v_inflow_from_bottom
+ v_inflow_from_left + v_inflow_from_right
- v_outflow) / (dx * dx)
# 拡散の増減値を加える計算。
du_lap = Du * laplacian_u
dv_lap = Dv * laplacian_v
u += du_lap
v += dv_lap
# `VISUALIZATION_STEP`回分拡散の更新が終わったら可視化を更新する。
visualizer.update(matrix=u)
※止める際にはinterrupt the kernrlなどで止めてください。
可視化されるものを眺めていると、以下のように初期値の正方形が(フォトショップなどのガウスぼかしを反映するように)拡散していくさまが確認できます。
この時点だと拡散のみで反応と流入の計算をしていないので、周囲に広がって薄くなるだけのアニメーションとなっています。
反応と流入・流出の計算
反応と流入・流出の計算を加えて、$\frac{\partial u}{\partial t}$と$\frac{\partial v}{\partial t}$の値を算出していきます。
式(1)における$uv^2 + f(1 - u)$と式(2)における$uv^2 - v(f + k)$の部分です。
といっても、fとkは固定の値なので、特に難しい計算ではありません。前述のdu_lapなどの変数部分の計算を以下のように書き換えるだけです($\frac{\partial u}{\partial t}$などはpartial_uとpartial_vという変数名にしました)。
...
partial_u = Du * laplacian_u - u * v * v + f * (1.0 - u)
partial_v = Dv * laplacian_v + u * v * v - v * (f + k)
u += partial_u
v += partial_v
...
これで完成です!
可視化してみると、以下のように模様が生まれます。
後は、kとfの値を変えたりすると、記事の最初に載せたような細胞分裂するようなアニメーションだったり、色々な変化が楽しめます。
コード全体
import os
import sys
import numpy as np
from alifebook_lib.visualizers import MatrixVisualizer
visualizer = MatrixVisualizer()
SPACE_GRID_SIZE = 256
VISUALIZATION_STEP = 8
dx = 0.01
Du = 2e-5
Dv = 1e-5
f = 0.022
k = 0.051
SQUARE_SIZE = 20
u = np.ones(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
v = np.zeros(shape=(SPACE_GRID_SIZE, SPACE_GRID_SIZE))
square_start = SPACE_GRID_SIZE // 2 - SQUARE_SIZE // 2
square_end = SPACE_GRID_SIZE // 2 + SQUARE_SIZE // 2
u[square_start:square_end, square_start:square_end] = 0.5
v[square_start:square_end, square_start:square_end] = 0.25
while True:
for i in range(VISUALIZATION_STEP):
# uのラプラシアンの算出。
u_inflow_from_top = np.roll(a=u, shift=1, axis=0)
u_inflow_from_bottom = np.roll(a=u, shift=-1, axis=0)
u_inflow_from_left = np.roll(a=u, shift=1, axis=1)
u_inflow_from_right = np.roll(a=u, shift=-1, axis=1)
u_outflow = 4 * u
laplacian_u = (u_inflow_from_top + u_inflow_from_bottom
+ u_inflow_from_left + u_inflow_from_right
- u_outflow) / (dx * dx)
# vのラプラシアンの算出。
v_inflow_from_top = np.roll(a=v, shift=1, axis=0)
v_inflow_from_bottom = np.roll(a=v, shift=-1, axis=0)
v_inflow_from_left = np.roll(a=v, shift=1, axis=1)
v_inflow_from_right = np.roll(a=v, shift=-1, axis=1)
v_outflow = 4 * v
laplacian_v = (v_inflow_from_top + v_inflow_from_bottom
+ v_inflow_from_left + v_inflow_from_right
- v_outflow) / (dx * dx)
# 拡散の増減値を加える計算。
partial_u = Du * laplacian_u - u * v * v + f * (1.0 - u)
partial_v = Dv * laplacian_v + u * v * v - v * (f + k)
u += partial_u
v += partial_v
# `VISUALIZATION_STEP`回分拡散の更新が終わったら可視化を更新する。
visualizer.update(matrix=u)
余談と感想
- 例の如く理系の人間ではないので、理解が微妙な点などのマサカリなどは弱めだと幸いです・・!
- なんだか、昔wonderflとかのフラッシュサイトの作品とか、PixelBenderとかのシェーダー関係のツールを触っていた頃を思い出して、とても楽しかったです
 (言語などが変わってもなんだか似たようなことをしている・・)
(言語などが変わってもなんだか似たようなことをしている・・)