TL;DR
- オートポイエーシスのうち、特にシンプルで簡単なSCLモデルをPythonで試します。
- 以下のようなアニメーションのものを作ります。
主な参考文献
また、上記書籍のgithubのリポジトリのコードもMITライセンスなので参照・利用させていただきますmm
※本記事では割愛した説明なども山ほどあるので、ALife関係の詳細は書籍をお買い求めください。
オートポイエーシスとは
オートポイエーシス (autopoiesis) は、1970年代初頭、チリの生物学者ウンベルト・マトゥラーナとフランシスコ・バレーラにより、「生命の有機構成 (organization) とは何か」という本質的問いを見定めるものとして提唱された、最先端のシステム論である。
...
特に細胞の代謝系や神経系に注目した彼らは、物質の種類を越えたシステムそのものとしての本質的な特性を、円環的な構成と自己による境界決定に認めた。
...
なお、オートポイエーシスという語はギリシャ語で自己製作 (ギリシャ語で auto, αυτό は自己、poiēsis, ποίησις は製作・生産・創作) を意味する造語であり、日本語ではしばしば自己創出、自己産出とも書かれる。
...
生命の究極の原理と目されるオートポイエーシスのコード化可能性についての議論は、社会へのAI応用が進むにつれて現実的な課題になりつつ有り、人工知能においては生命の脳の構造をコンピュータ上に複写するだけでは自律性として不十分か否か,人工生命においては、真に自律的な人工生命はソフトウェア化可能か否かという課題に関わって来ている[2]。
オートポイエーシス - Wikipedia
例えば、細胞が自らを生成し、細胞膜を使って維持できるものなどが一例として該当します。
SCLモデルとは
オートポイエーシスのモデルの一つで、概念を理解するための簡単な例です。
「個の双発とは何か?」という問いに対し、SCLモデルは、「自己の存在を決定するのはそれ自体の構成するプロセスによってである」というひとつの理解の仕方を提示しています。
作って動かすALife ―実装を通した人工生命モデル理論入門 P58より引用
オートポイエーシスは、「真の自律性をコード化することは可能か?」といった観点から哲学的に様々な議論が行われている最中であるが、1974年の提唱者らの研究によれば、少なくともSCLモデルとしてコード化し、シミュレーションを行うことは可能とされている[1]。
オートポイエーシス - Wikipedia
プログラムで組んでみると、前出のアニメーションのように、各要素が反応しながら、膜を作ったりと反応していくモデルになります。
それぞれ、以下の頭文字にモデルの名前が由来します。
S : Substrate(基質)
辞書を引くと以下のようになっています。
《生化学》基質◆酵素が媒介して生化学反応を起こさせる物質。
substrateとは
今回のモデルだと、他の要素を触媒として、膜を生成したりします。
アニメーションの中では、水色の○が該当します。
C : Catalyst(触媒)
基質(Substrate)が膜に変化する際に触媒となる要素です。
アニメーションの中では紫の○が該当します。
L : Link(膜)
基質(S)が触媒(C)を使って生成される膜です。
細胞膜のように、触媒要素を囲んだりもします(触媒要素が動かなくなる)。
隣接する膜同士で連結したり、基質(S)を吸収したり、放出したり、さらには連結を解除したり基質に戻ったりも反応の中で発生します。
アニメーションの中では青い四角や四角同士を連結する線が該当します。
発生する反応・変化
基質から膜への変化
2つの基質(S)と1つの触媒(C)が反応して、一つの膜(L)と1つの触媒(C)に変化します。
式で表すと以下のようになります。
\tag{式1}
2S + C → L + C
英語ではproduction(算出)という単語で以降のコードなどで扱います。
膜から基質への変化
1つの膜(L)が2つの基質に変化します。この変化には触媒(C)は不要です。
式で表すと以下のようになります。
\tag{式2}
L → 2S
英語ではdisintegration(崩壊)という単語で以降のコードなどで扱います。
膜の結合
2つの膜(L)同士が結合します。アニメーションでは、四角同士が線で繋がっている状態です。
英語ではbonding(結合)という単語で以降のコードなどで扱います。
膜の結合の崩壊
連結している(bonding)2つの膜(L)の連結が解除されます。
英語ではbond decay(結合の崩壊)という単語で以降のコードなどで扱います。
膜による基質の吸収
膜(L)が基質(S)を吸収します。
膜と基質が合体したような状態になります。
英語ではこの変化自体をabsorption(吸収)、変化後の要素をLINK_SUBSTRATEという単語で以降のコードでなどで表記します。
膜による基質の放出
基質を吸収した膜(LINK_SUBSTRATE)が基質(S)を放出する変化です。
近傍の空いている領域に放出します。
英語ではemission(放出)という単語で以降のコードなどで表記します。
Pythonでの実装
使う環境
- Windows
- Python 3.6.8
- NumPy==1.14.5
- Vispy==0.5.3
- JupyterLab(及びjupyterlab-lsp)
-
前述の書籍のgithubのコード
- ※事前にcloneしてimportできるようにしておきます。可視化でalifebook_lib以下のモジュールを利用します。
初期設定や可視化ライブラリの挙動の確認
まずは必要なモジュールをimportします。
書籍のコードでSCLVisualizerという、SCLモデルのための可視化のモジュールが用意されているので利用します。
from typing import Dict, List
import numpy as np
from alifebook_lib.visualizers import SCLVisualizer
visualizer = SCLVisualizer()
空間のサイズを指定します。今回は縦横16x16のグリッド空間を使います。
SPACE_SIZE = 16
続いて粒子(分子)関係のクラスなどを用意します。今回、1つの基質(S)や触媒(C)、膜(L)などを分子1つ分として扱います(以降では、基質分子や膜分子などとも表記していきます)。
それぞれの種別も定数で定義しておきます。
分子が1つも無いグリッドの箇所は種別値としてはHOLE(空)として扱います。
TYPE_NAME_SUBSTRATE = 'SUBSTRATE'
TYPE_NAME_CATALYST = 'CATALYST'
TYPE_NAME_LINK = 'LINK'
TYPE_NAME_LINK_SUBSTRATE = 'LINK_SUBSTRATE'
TYPE_NAME_HOLE = 'HOLE'
TYPE_NAME_LIST = [
TYPE_NAME_SUBSTRATE,
TYPE_NAME_CATALYST,
TYPE_NAME_LINK,
TYPE_NAME_LINK_SUBSTRATE,
TYPE_NAME_HOLE,
]
class Bond:
"""
膜分子の結合情報単体を扱うクラス。
Attributes
----------
to_x : int
結合先のX座標。
to_y : int
結合先のY座標。
"""
def __init__(self, to_x: int, to_y: int):
self.to_x = to_x
self.to_y = to_y
Bondクラスは、膜(L)の結合先の情報のみを扱います。
class Particle:
"""
分子1つ分のオブジェクトを生成するクラス。
Attributes
----------
type_name : str
分子の種別値名。
is_disintegrated : bool
崩壊済みかどうか。膜分子のみ設定される。もしTrueの場合、
基質(S)分子が放出可能(近傍に空いているグリッドが2つ
存在する等)な場合に膜分子から基質への変化が実行される。
もし放出が出来ない条件(近傍に空いているグリッドが存在
しない等)の場合には、この真偽値は引き継がれ、次回の
タイミングで放出可能かどうかがチェックされる。
bonds : list of Bonds
膜の結合先の情報を格納したリスト。
"""
def __init__(
self, type_name_: str, is_disintegrated: bool, bonds: list):
self.type_name: str = type_name_
self.is_disintegrated: bool = is_disintegrated
self.bonds: List[Bond] = bonds
@property
def type_name(self) -> str:
return self._type_name
@type_name.setter
def type_name(self, value: str):
"""
種別値名。
Parameters
----------
value : str
設定する種別値名。
Raises
------
ValueError
定義されていない種別値が指定された場合。
"""
is_in = value in TYPE_NAME_LIST
if not is_in:
err_msg = '定義されていない種別値が指定されています : %s' \
% value
raise ValueError(err_msg)
self._type_name = value
Particleクラスは分子一つ分を扱います。基質(S)なのか触媒(C)なのか膜なのか(L)などの種別値や、崩壊済み(膜から基質に変化する状態)かどうかの真偽値、後は膜の場合の連結先の情報のリストを属性に持ちます。
可視化方面に関して、ライブラリモジュールの内容把握のために色々試してみます。
まず、前述の各クラスを可視化用のデータに変換するための関数を用意しておきます。
最初から可視化用のデータで扱えばいいのでは?という感じも少ししますが、補完が効いたりエラーハンドリングなどでミスを減らせそう(コード量も多くなりそう)なので、可視化用に変換の関数を挟むようにして進めます。
def to_visualizer_bonds(bonds: list) -> list:
"""
可視化で必要なフォーマットに、膜(L)の連結情報のリストを
変換する。
Parameters
----------
bonds : list of bond
変換対象のリスト。
Returns
-------
visualizer_bonds : list of dicts
可視化用のフォーマットに変換された連結情報のリスト。
"""
visualizer_bonds = []
bond: Bond
for bond in bonds:
bond_tuple = (bond.to_y, bond.to_x)
visualizer_bonds.append(bond_tuple)
return visualizer_bonds
to_visualizer_bonds関数は、膜(L)の連結情報を可視化用のフォーマットに変換します。
可視化にはy座標とx座標を格納するtupleを格納したリストが必要となります。
def to_visualizer_arr_from_particles(particles: np.array) -> np.array:
"""
分子の行列のデータを、可視化で必要なフォーマットに変換する。
Parameters
----------
particles : np.array
変換対象の分子のオブジェクトを格納した2次元配列。
Returns
-------
visualiser_arr : np.array
変換された可視化用の配列。
"""
visualiser_arr = np.empty(shape=(SPACE_SIZE, SPACE_SIZE), dtype=object)
particle: Particle
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particle = particles[row, column]
visualiser_arr[row, column] = {
'type': particle.type_name,
'disintegrating_flag': particle.is_disintegrated,
'bonds': to_visualizer_bonds(bonds=particle.bonds),
}
return visualiser_arr
続いて、分子のオブジェクトを格納した行列を可視化用に変換する関数です。
クラスではなく辞書が必要で、ライブラリ側で辞書に以下のキーが必要なので設定しています。
- type : str
- disintegrating_flag : bool
- bonds : list of tuple
可視化のための準備が終わったので実際に試してみます。
分子の行列は、SPACE_SIZE × SPACE_SIZEのサイズで作る必要があります。
まずは全て気質分子(S)で初期化して可視化してみます(TYPE_NAME_SUBSTRATEを指定します)。
particles = np.empty(shape=(SPACE_SIZE, SPACE_SIZE), dtype=object)
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_SUBSTRATE, is_disintegrated=False, bonds=[])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
SPACE_SIZE分のグリッド(16 x 16)に水色の○(基質分子)が配置されました。
空の際の表示の確認のため、下半分にTYPE_NAME_HOLEを指定してみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
if row <= SPACE_SIZE // 2 - 1:
particles[row, column] = Particle(
type_name_=TYPE_NAME_SUBSTRATE, is_disintegrated=False, bonds=[])
else:
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように、TYPE_NAME_HOLEを指定した箇所は何も表示されなくなります。
左上の位置に触媒分子(C)を1つ設定し、可視化してみます。
particles[0, 0] = Particle(
type_name_=TYPE_NAME_CATALYST, is_disintegrated=False,
bonds=[])
以下のように、基質分子よりも少し大きめの紫の○が追加になります。
触媒分子は、基質分子よりも大分少ない数が配置されるので、目立つ感じになっています。
続いて膜分子です。一番上の行の2列目、3列目に設定してみます。
particles[0, 1] = Particle(
type_name_=TYPE_NAME_LINK, is_disintegrated=False, bonds=[])
particles[0, 2] = Particle(
type_name_=TYPE_NAME_LINK, is_disintegrated=False, bonds=[])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように青い□で表示されます。
膜の連結(bond)設定をしてみます。連結する膜分子同士で、両方に連結先をbonds引数に設定します。
particles[0, 1] = Particle(
type_name_=TYPE_NAME_LINK, is_disintegrated=False,
bonds=[Bond(to_x=2, to_y=0)])
particles[0, 2] = Particle(
type_name_=TYPE_NAME_LINK, is_disintegrated=False,
bonds=[Bond(to_x=1, to_y=0)])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように□の間に線が設定され、□-□みたいな表示になりました。
可視化の最後の確認として、基質を吸収した膜分子(LINK_SUBSTRATE)の表示を確認してみます。
最初の列の4列目([0, 3])に設定します。
particles[0, 3] = Particle(
type_name_=TYPE_NAME_LINK_SUBSTRATE, is_disintegrated=False,
bonds=[])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
青い□(膜)の中に水色の○(基質)がある形です。そのままで分かりやすいですね。
近傍の話と実装
計算の過程で周囲のグリッドを参照します。
そのため、ノイマン近傍の取得処理とムーア近傍の取得処理に絡んだ関数を用意しておきます。
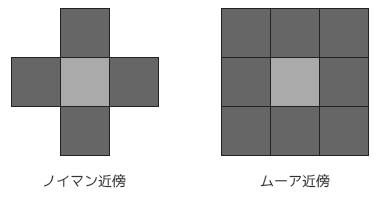
ノイマン(neumann)近傍は、対象のセルの上下左右の4つのセルのことを言います。
ムーア(moore)近傍は、ノイマン近傍に追加して、斜めの領域を含めた8つのセルのことを言います。
まずはノイマン近傍の4つの座標を格納したリストを取得する関数を用意します。
def get_neumann_neighborhood_list(x, y):
"""
指定された座標のノイマン近傍の4つの座標を格納したリストを取得する。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
neumann_neighborhood_list : list of tuple
ノイマン近傍の4つの座標を格納したリスト。右・左・下・上の順番で
格納される。
"""
neumann_neighborhood_list = [
((x + 1) % SPACE_SIZE, y),
((x - 1) % SPACE_SIZE, y),
(x, (y + 1) % SPACE_SIZE),
(x, (y - 1) % SPACE_SIZE),
]
return neumann_neighborhood_list
以下のような返却値が返されます。
get_neumann_neighborhood_list(x=5, y=3)
[(6, 3), (4, 3), (5, 4), (5, 2)]
(余談ですが、剰余ってマイナスでも動作するのですね・・・(今更))
ノイマン近傍のうちの1つの座標をランダムに選択する関数を追加します。
def get_random_neumann_neighborhood(x, y):
"""
指定された座標のノイマン近傍のうち、ランダムに1つの座標を返す。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
neumann_x : int
算出されたノイマン近傍のx座標。
neumann_y : int
算出されたノイマン近傍のy座標。
"""
neumann_neighborhood_list = get_neumann_neighborhood_list(x=x, y=y)
random_index = np.random.randint(
low=0,
high=len(neumann_neighborhood_list))
neumann_x = neumann_neighborhood_list[random_index][0]
neumann_y = neumann_neighborhood_list[random_index][1]
return neumann_x, neumann_y
以下のように、実行の度にランダムなノイマン近傍が選択されます。
get_random_neumann_neighborhood(x=5, y=3)
(5, 4)
get_random_neumann_neighborhood(x=5, y=3)
(4, 3)
ムーア近傍の8つの座標のリストを取得する関数も追加します。
def get_moore_neighborhood_list(x, y):
"""
指定された座標のムーア近傍の8つの座標を格納したリストを取得する。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_neighborhood_list : list of tuple
ムーア近傍の8つの座標を格納したリスト。左上・上・右上・左・中央・右・
左下・下・右下の順番に格納される。
"""
left_x = (x - 1) % SPACE_SIZE
right_x = (x + 1) % SPACE_SIZE
upper_y = (y - 1) % SPACE_SIZE
lower_y = (y + 1) % SPACE_SIZE
moore_neighborhood_list = [
(left_x, upper_y),
(x, upper_y),
(right_x, upper_y),
(left_x, y),
(right_x, y),
(left_x, lower_y),
(x, lower_y),
(right_x, lower_y),
]
return moore_neighborhood_list
以下のような値が返ってきます。
get_moore_neighborhood_list(x=3, y=5)
[(2, 4), (3, 4), (4, 4), (2, 5), (4, 5), (2, 6), (3, 6), (4, 6)]
ノイマン近傍同様、ムーア近傍にも同様に近傍の中からランダムに1つの座標を選択する関数を追加します。
def get_random_moore_neighborhood(x, y):
"""
指定された座標のムーア近傍のうち、ランダムに1つの座標を返す。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_x : int
算出されたムーア近傍のx座標。
moore_y : int
算出されたムーア近傍のy座標。
"""
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
random_index = np.random.randint(
low=0, high=len(moore_neighborhood_list))
moore_x = moore_neighborhood_list[random_index][0]
moore_y = moore_neighborhood_list[random_index][1]
return moore_x, moore_y
以下のような値が返ってきます。
get_random_moore_neighborhood(x=3, y=5)
(4, 6)
get_random_moore_neighborhood(x=3, y=5)
(3, 4)
次の関数として、ムーア近傍の中から座標を2つ取得する関数を追加します。
ただし、その2つの近傍は隣接する(ノイマン近傍内)という条件を設けます。
この関数は後述する計算で必要になります。
前述の条件だと、最初に選択された1つめのムーア近傍の座標に応じて3パターンの分岐が必要になります。
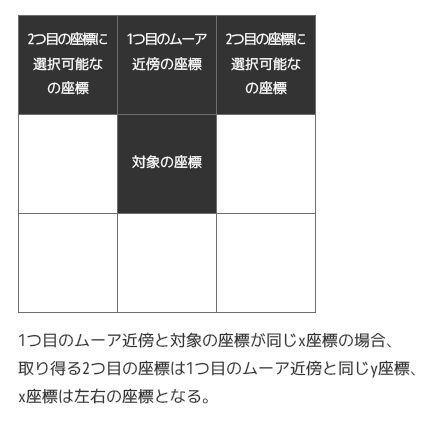
初見の時、関数のコードを読んでいて少し考えていたのですが、図にするとシンプルにさくっと理解できます。
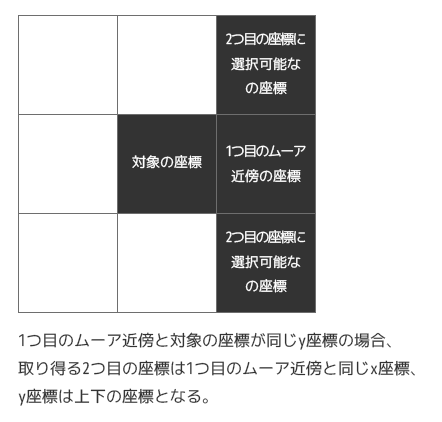
[1]. 1つ目のムーア近傍の座標が、対象の座標とx座標が一緒の場合 :
[2]. 1つ目のムーア近傍の座標が、対象の座標とy座標が一緒の場合 :
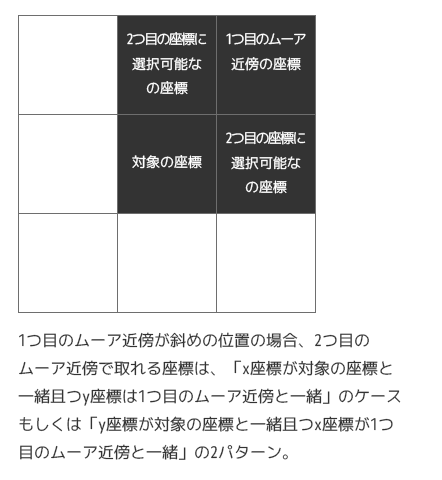
[3]. 前述の2つの条件に該当しない(1つ目のムーア近傍の座標が斜めの位置の)場合 :
def get_random_2_moore_neighborhood(x, y):
"""
指定された座標のムーア近傍のうち、ランダムに2つの座標を取得する。
2つの近傍の座標はそれぞれ隣接している座標の中から算出される。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_x_1 : int
1つ目のムーア近傍のx座標。
moore_y_1 : int
1つ目のムーア近傍のy座標。
moore_x_2 : int
2つ目のムーア近傍のx座標。
moore_y_2 : int
2つ目のムーア近傍のy座標。
"""
moore_x_1, moore_y_1 = get_random_moore_neighborhood(x=x, y=y)
if x == moore_x_1:
moore_x_2 = np.random.choice([
(moore_x_1 - 1) % SPACE_SIZE,
(moore_x_1 + 1) % SPACE_SIZE,
])
moore_y_2 = moore_y_1
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
if y == moore_y_1:
moore_x_2 = moore_x_1
moore_y_2 = np.random.choice([
(moore_y_1 - 1) % SPACE_SIZE,
(moore_y_1 + 1) % SPACE_SIZE,
])
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
choice = [(x, moore_y_1), (moore_x_1, y)]
random_index = np.random.randint(0, 2)
moore_x_2, moore_y_2 = choice[random_index]
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
上記の関数で以下のような値が返ります。
get_random_2_moore_neighborhood(x=3, y=5)
(2, 6, 2, 5)
get_random_2_moore_neighborhood(x=3, y=5)
(3, 4, 2, 4)
get_random_2_moore_neighborhood(x=3, y=5)
(4, 4, 4, 5)
続いて、対象の座標のムーア近傍の座標に隣接する2つの座標を取得する関数を用意します。
ムーア近傍に隣接する座標が返却されるので、最初に選択されたムーア近傍の座標自体は返却されません。
また、返却される2つの座標は最初に指定された座標のムーア近傍のリストからのみ選択されます。
結果的に、返却される2つの座標は、与えられた座標とムーア近傍の組み合わせで1つの座標のセットのみが存在します。
(前述の関数のように、ランダムに座標を選んだりはしません)
文章だけだとなんだか私の頭ではよく分からない・・・ので、こちらも図にしてみます(図にするととてもシンプル)。
この関数も、指定された座標と最初のムーア近傍の座標のxが一緒か、yが一緒か、もしくは両方とも違うかの3パターンが存在します。
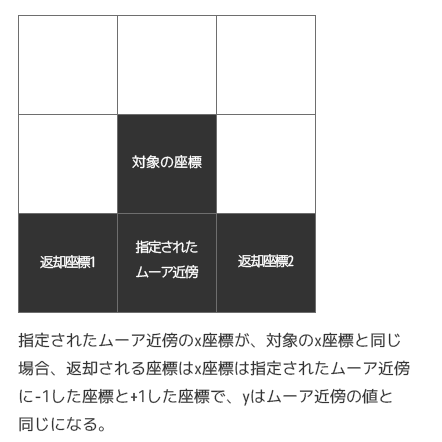
[1]. 指定されたムーア近傍のx座標が、対象の座標のx座標と一緒の場合 :
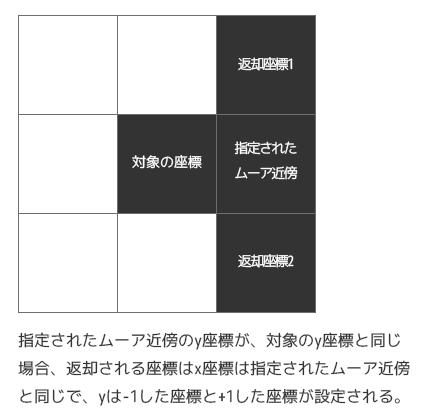
[2]. 指定されたムーア近傍のy座標が、対象の座標のy座標と一緒の場合 :
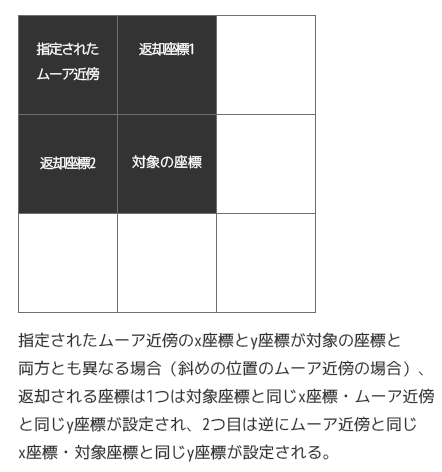
[3]. 指定されたムーア近傍のx座標とy座標の両方が、対象の座標のx座標とy座標両方と異なる場合(斜めのムーア近傍の座標の場合) :
def get_adjacent_2_moore_neighborhood(x, y, moore_x, moore_y):
"""
指定された対象座標とそのムーア近傍に隣接した2つの座標を取得する。
返却される2つの座標は、指定された座標のムーア近傍が設定される。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
moore_x : int
対象座標のムーア近傍のx座標。
moore_y : int
対象座標のムーア近傍のy座標。
Returns
-------
adjacent_x_1 : int
算出された1つ目のムーア近傍に隣接したx座標。
adjacent_y_1 : int
算出された1つ目のムーア近傍に隣接したy座標。
adjacent_x_2 : int
算出された2つ目のムーア近傍に隣接したx座標。
adjacent_y_2 : int
算出された2つ目のムーア近傍に隣接したy座標。
"""
if x == moore_x:
adjacent_x_1 = (moore_x - 1) % SPACE_SIZE
adjacent_y_1 = moore_y
adjacent_x_2 = (moore_x + 1) % SPACE_SIZE
adjacent_y_2 = moore_y
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
if y == moore_y:
adjacent_x_1 = moore_x
adjacent_y_1 = (moore_y - 1) % SPACE_SIZE
adjacent_x_2 = moore_x
adjacent_y_2 = (moore_y + 1) % SPACE_SIZE
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
adjacent_x_1 = x
adjacent_y_1 = moore_y
adjacent_x_2 = moore_x
adjacent_y_2 = y
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
実行すると以下のように返却値が返ってきます。
引数に応じて、返却される値は固定です。
get_adjacent_2_moore_neighborhood(x=3, y=5, moore_x=3, moore_y=6)
(2, 6, 4, 6)
get_adjacent_2_moore_neighborhood(x=3, y=5, moore_x=4, moore_y=5)
(4, 4, 4, 6)
get_adjacent_2_moore_neighborhood(x=3, y=5, moore_x=4, moore_y=6)
(3, 6, 4, 5)
各反応(変化)のための実装
ここからは、各分子などの反応(変化)部分のための実装を進めます。
まずは反応や変化で参照されるパラメーターを設定します。
要素(分子)の移動する / しないに影響するパラメーターとして、MOBILITY_FACTORという辞書で設定していきます。
この値が大きい要素ほど移動しやすくなります。
MOBILITY_FACTOR: Dict[str, float] = {
TYPE_NAME_HOLE: 0.1,
TYPE_NAME_SUBSTRATE: 0.1,
TYPE_NAME_CATALYST: 0.0001,
TYPE_NAME_LINK: 0.05,
TYPE_NAME_LINK_SUBSTRATE: 0.05,
}
計算が実際に発生する確率は、
\sqrt{座標1の分子のパラメーター × 座標2の分子のパラメーター}
で算出します。
例えば1つ目がHOLEで、2つ目がSUBSTRATEの場合は、
np.sqrt(MOBILITY_FACTOR[TYPE_NAME_HOLE] * MOBILITY_FACTOR[TYPE_NAME_SUBSTRATE])
で0.1(10%)となります($\sqrt{0.1 × 0.1} = 0.1$)。
結果として、基質はよく動きます。
逆に触媒(C)は上記の例ではあまり動かなくなります。CATALYSTとSUBSTRATEであれば、
np.sqrt(MOBILITY_FACTOR[TYPE_NAME_CATALYST] * MOBILITY_FACTOR[TYPE_NAME_SUBSTRATE])
で0.003162...となります($\sqrt{0.0001 × 0.1} = 0.003162...$)。
続いてproductionやbondingなどの各反応の起こりやすさの確率のパラメーターを設定します。
この値が大きいほど、後で実装する反応の処理が発生しやすくなります。
PROBABILITY_PRODUCTION = 0.95
PROBABILITY_DISINTEGRATION = 0.0005
PROBABILITY_BONDING_CHAIN_INITIATE = 0.3
PROBABILITY_BONDING_CHAIN_EXTEND = 0.3
PROBABILITY_BONDING_CHAIN_SPLICE = 0.9
PROBABILITY_BOND_DECAY = 0.0005
PROBABILITY_ABSORPTION = 0.5
PROBABILITY_EMISSION = 0.5
基質から膜への変化(production)などは起こりやすく、膜から基質への変化(disintegration)や膜同士の結合が無くなる変化(bond_decay)などは起こりづらい、といったところでしょうか。
実際には、各反応のための条件が揃っている上でさらに確率による評価がされるので、実際の確率はここで定義された値よりも低くなります。
また、確率評価用の関数も用意します。これは、与えられた確率に応じて、TrueもしくはFalseを返すだけの関数です。
def evaluate_probability(probability: float) -> bool:
"""
確率probabilityに応じて、TrueもしくはFalseを返す。
Parameters
----------
probability : float
評価対象の確率。
Returns
-------
bool
確率に応じた真偽値が設定される。
"""
return np.random.rand() < probability
例えば、確率に0.8を指定して大量に実行すれば、大数の法則的に大体8:2の割合でTrueとFalseが返ります。
true_num = 0
false_num = 0
for i in range(100000):
if evaluate_probability(probability=0.8):
true_num += 1
else:
false_num += 1
true_num
79944
false_num
20056
production(基質分子から膜分子への変化)の実装
2つの基質(S)と1つの触媒(C)によって、基質が膜(L)に変化する反応を実装します。
def production(particles: np.array, x: int, y: int):
"""
条件を満たした場合に、2つの基質分子(S)を1つの膜分子(L)に
変化させる。以下の条件で判定が実行される。
- 指定された座標の分子が触媒分子(C)であること。
- 指定された座標のランダムなムーア近傍を2つ選択し、それらの座標が
基質分子であること。
- ※2つのムーア近傍は隣接している必要がある。
- production発生確率を評価し、Trueが返却されること。
変化後として、以下のような変化が設定される。
- 1つ目のムーア近傍の座標は空(HOLE)になる。
- 2つ目のムーア近傍の座標は膜(L)になる。
Parameters
----------
particles : array-like
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_CATALYST:
return
moore_x_1, moore_y_1, moore_x_2, moore_y_2 = \
get_random_2_moore_neighborhood(x=x, y=y)
moore_particle_1: Particle = particles[moore_y_1, moore_x_1]
if moore_particle_1.type_name != TYPE_NAME_SUBSTRATE:
return
moore_particle_2: Particle = particles[moore_y_2, moore_x_2]
if moore_particle_2.type_name != TYPE_NAME_SUBSTRATE:
return
if not evaluate_probability(probability=PROBABILITY_PRODUCTION):
return
moore_particle_1.type_name = TYPE_NAME_HOLE
moore_particle_2.type_name = TYPE_NAME_LINK
試しに、手動で動かしてみます。
まずは変化が分かりやすいように全て基質分子(S)に更新してしまいます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_SUBSTRATE, is_disintegrated=False, bonds=[])
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
続いて、反応のためには触媒分子(C)が必要なので、任意の座標を触媒分子に更新します。
x = 2
y = 1
particles[y, x].type_name = TYPE_NAME_CATALYST
particle_data = to_visualizer_arr_from_particles(particles=particles)
visualizer.update(particle_data=particle_data)
その触媒分子(C)の座標に対して何度か手動でproductionの処理を流してみます。
反応が発生し、空(HOLE)の座標と膜(L)の座標が発生しました。
何度か実行してみると、まだ膜になれる(複数の基質分子が近傍に存在する)ため、膜がどんどん増えていきます。
確率による判定もされるので、反応しない時もあります。
最終的に上記のようになりました。まだ近傍に2つ基質が残っていますが、反応の際に「選択される2つのムーア近傍は隣接している必要がある」という条件があるため、これ以上は変化は発生しません。
emission(基質を含んだ膜の、基質の放出の反応)の実装
順番がリスト通りではないですが、disintegrationでemissionの反応を使ったりするので、先にこちらを実装します。
基質(S)を吸収している膜分子(LINK_SUBSTRATE)が、基質を空いている近傍に放出する反応となります。
反応後、LINK_SUBSTRATEはただの膜(LINK)になり、空いている近傍は基質分子(S)となります。
def emission(
particles: np.array, x: int, y: int,
probability: float=PROBABILITY_EMISSION):
"""
基質(S)を吸収した膜分子(LINK_SUBSTRATE)で、基質を放出する
反応を実行する。以下の条件を満たした場合に実行される。
- 対象の座標の分子が基質(S)を吸収した膜分子(LINK_SUBSTRATE)
であること。
- ランダムに選択したムーア近傍が、空(HOLE)であること。
- 指定された確率を評価して、Trueが返ること。
変化後として、以下のような変化が設定される。
- LINK_SUBSTRATE から膜(LINK)に変化する。
- 空(HOLE)の近傍座標は基質(S)に変化する。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_LINK_SUBSTRATE:
return
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_HOLE:
return
if not evaluate_probability(probability=probability):
return
particle.type_name = TYPE_NAME_LINK
moore_particle.type_name = TYPE_NAME_SUBSTRATE
引数にprobabilityを設けていますが、これは自然に実行される際に参照される、定数として定義されている確率以外にも、他の反応時に1.0の確率でemissionさせたりする必要があるためです。
手動で動かして試してみます。
まずは、近傍が空(HOLE)で且つ基質を吸収した膜分子(TYPE_NAME_LINK_SUBSTRATE)が必要なので、グリッドの各セルを一旦全て空にして1箇所のみTYPE_NAME_LINK_SUBSTRATEに変更して可視化してみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
x = 2
y = 1
particles[y, x].type_name = TYPE_NAME_LINK_SUBSTRATE
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
続いて、emissionの反応を実行して可視化してみます。
emission(particles=particles, x=x, y=y, probability=1.0)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
基質が外に出ました。問題なく動いていそうです。
bond_decay(膜の結合の消滅)の実装
こちらも順番通りではないのですが、disintegrationの反応で必要なので先に実装しておきます。
bond_decayは、膜分子(L)同士の結合(連結)が無くなる反応です。
一定確率で結合が消滅します。
def bond_decay(
particles: np.array, x: int, y: int,
probability: float=PROBABILITY_BOND_DECAY):
"""
膜分子(L)同士の結合を一定確率で消滅させる。以下の条件を満たす
場合に実行される。
- 対象座標の分子が膜(L)もしくは基質を吸収した膜(LINK_SUBSTRATE)
である。
- 与えられた確率を評価し、Trueが返ること。
変化後として、対象座標に設定されている結合設定(bonds)が空になる。
結合先の結合設定も同様に削除される。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
probability : float, default PROBABILITY_BOND_DECAY
反応の発生確率。
"""
particle: Particle = particles[y, x]
if particle.type_name not in (TYPE_NAME_LINK, TYPE_NAME_SUBSTRATE):
return
if not evaluate_probability(probability=probability):
return
bond: Bond
for bond in particle.bonds:
neighbor_particle: Particle = particles[bond.to_y, bond.to_x]
neighbor_bond: Bond
for neighbor_bond in neighbor_particle.bonds:
if neighbor_bond.to_x != x or neighbor_bond.to_y != y:
continue
# 結合先の膜分子側の結合情報を削除する。
neighbor_particle.bonds.remove(neighbor_bond)
break
particle.bonds = []
手動で動かしてみます。
まずは各分子を空(HOLE)にして、特定の3つの座標のみ膜分子(L)に変更し、bond_decayではそれぞれが結合している(bonds属性にデータが入っている)必要があるので、結合させておきます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
particle_1: Particle = particles[1, 1]
particle_2: Particle = particles[1, 2]
particle_3: Particle = particles[2, 2]
particle_1.type_name = TYPE_NAME_LINK
particle_2.type_name = TYPE_NAME_LINK
particle_3.type_name = TYPE_NAME_LINK
particle_1.bonds = [Bond(to_x=2, to_y=1)]
particle_2.bonds = [Bond(to_x=1, to_y=1), Bond(to_x=2, to_y=2)]
particle_3.bonds = [Bond(to_x=2, to_y=1)]
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
続いて、2つの座標に結合している座標の膜分子に対して、bond_decayを反映してみます。
bond_decay(particles=particles, x=2, y=1, probability=1.0)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
結合が無くなりました。
disintegration(膜分子から基質分子への変化)の実装
disintegrationはproduction(基質分子(S)から膜分子(L)への変化)の逆となる反応です。
1つの膜分子(L)から、2つの基質分子(S)に変化します。
また、膜分子は基質を吸収した状態(LINK_SUBSTRATE)である場合があります。
その場合には、吸収されている基質も一緒に放出されます(実質3つの基質に変化する時があります)。
他の膜分子と結合している際には、その結合も解除されます。
def disintegration(particles, x, y):
"""
膜分子(L)から2つの基質分子(S)に変化する反応を実行する。
以下の条件を満たした場合に実行される。
- 対象の座標が膜分子(L)もしくは基質を吸収した膜分子
(LINK_SUBSTRATE)である。
- 確率評価の結果Trueが返却された。
- 基質を吸収している場合には、放出済みである。
- ランダムに選択したムーア近傍の座標が空(HOLE)である。
変化後として、以下のような変化が設定される。
- 基質分子を吸収している場合には放出される(emission)。
- 対象座標は基質分子となり、ムーア近傍にも1つ基質分子が発生する。
- 結合している場合には結合は解除される(bond_decay)。
Notes
-----
基質の放出や2つの基質への変化の都合、条件によっては即時で
反応を発生させることができないケースがある(近傍が埋まっていて
放出ができない場合など)。
そのような場合には、反応が実施されるフラグ(is_disintegrated)
はTrueのままなので、繰り返し反応が完了するまで実行される。
(一度確率を評価してフラグがTrueになった場合は、その後は反応が
起きるまでずっと反応が試みられる)
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name in (TYPE_NAME_LINK, TYPE_NAME_LINK_SUBSTRATE):
if evaluate_probability(probability=PROBABILITY_DISINTEGRATION):
particle.is_disintegrated = True
if not particle.is_disintegrated:
return
# 基質分子を吸収している場合には放出する。
emission(particles=particles, x=x, y=y, probability=1.0)
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
# 基質の放出などが完了していない場合などには処理を行わない。
if particle.type_name != TYPE_NAME_LINK:
return
if moore_particle.type_name != TYPE_NAME_HOLE:
return
bond_decay(particles=particles, x=x, y=y, probability=1.0)
particle.type_name = TYPE_NAME_SUBSTRATE
moore_particle.type_name = TYPE_NAME_SUBSTRATE
particle.is_disintegrated = False
他と同様に手動で動かして確認してみます。まずはシンプルに膜分子(Link)を1つだけ配置された状態にして確認してみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
x = 2
y = 1
particles[y, x].type_name = TYPE_NAME_LINK
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
また、disintegrationの反応自体がかなり発生しづらい確率が設定されている(PROBABILITY_DISINTEGRATION = 0.0005)ので、確認のため一時的に高い確率を設定しておきます(後で直します)。
PROBABILITY_DISINTEGRATION = 1.0
反応を実行してみます。
disintegration(particles=particles, x=x, y=y)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
想定通り膜分子から、2つの基質に変化しました。
膜分子同士の結合も解除される挙動が正しいので、結合設定をしてみて試してみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
particle_1 = particles[1, 1]
particle_1.type_name = TYPE_NAME_LINK
particle_1.bonds = [Bond(to_x=2, to_y=1)]
particle_2 = particles[1, 2]
particle_2.type_name = TYPE_NAME_LINK
particle_2.bonds = [Bond(to_x=1, to_y=1)]
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
disintegration(particles=particles, x=2, y=1)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
結合も同時に消滅しているのが分かります。
続いて、周囲に空いているセルが無いケースを試して見ます。
disintegrationの反応では、基質を放出したりが必要になるため、周囲を囲まれていると反応が発生しません(空いている領域が出来たら早い段階で放出などがされる)。
下記のような状況は発生しませんが、分かりやすいように周囲を触媒分子(C)で囲んで試してみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
x = 2
y = 1
particles[y, x].type_name = TYPE_NAME_LINK_SUBSTRATE
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
moore_neighborhood: tuple
for moore_x, moore_y in moore_neighborhood_list:
moore_particle: Particle = particles[moore_y, moore_x]
moore_particle.type_name = TYPE_NAME_CATALYST
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
反応の関数を実行してみます。
disintegration(particles=particles, x=x, y=y)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
上記を何度実行しても、反応は起きずそのままの状態が続くことが分かります。
ある程度挙動の確認はできたので、最後に一時的に調整した確率を元に戻しておきます。
PROBABILITY_DISINTEGRATION = 0.0005
absorption(膜分子(L)による基質分子(S)の吸収)の実装
absorptionはemissionの逆の反応で、膜(L)が基質(S)を吸収する反応となります。
def absorption(particles: np.array, x: int, y: int):
"""
膜分子(L)が近傍に存在する基質分子(S)を吸収し、LINK_SUBSTRATE
に変化する反応を実行する。以下の条件を満たす場合に実行される。
- 対象座標が膜分子であること。
- ランダムに選択したムーア近傍の座標が、基質分子であること。
- 確率を評価してTrueが返ること。
変化後として、以下のような変化が設定される。
- 膜分子(L)はLINK_SUBSTRATEになる。
- 基質分子(S)は空(HOLE)になる。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_LINK:
return
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_SUBSTRATE:
return
if not evaluate_probability(probability=PROBABILITY_ABSORPTION):
return
particle.type_name = TYPE_NAME_LINK_SUBSTRATE
moore_particle.type_name = TYPE_NAME_HOLE
手動で試します。
反応が起きやすいように膜分子(L)の近傍を基質分子(S)で囲んだ状態を作ります。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
x = 2
y = 1
particles[y, x].type_name = TYPE_NAME_LINK
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
for moore_x, moore_y in moore_neighborhood_list:
moore_particle = particles[moore_y, moore_x]
moore_particle.type_name = TYPE_NAME_SUBSTRATE
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
反応の関数を呼び出してみます。確率的に反応してくれないケースもありますが、何度か実行すると反応してくれます。
absorption(particles=particles, x=x, y=y)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
近傍の基質が1つ消滅し、膜分子(L)からLINK_SUBSTRATEに変化しました。
bonding(膜同士の結合)の実装
最後の山場です。膜(L)同士の結合のbondingの実装をします。
結構条件が多く、コードも長めです(初見でさくっと写経した時は理解が及ばないところが出てきたので、細かく見ていこうと思います)。
以下のような条件があります。
- 膜分子(L)は結合を2つまで持てる。3つ目は持てない(1つ目の膜分子側でも、2つ目の膜分子側でも、どちらかが既に2つ結合を持っていれば結合はできない)。
- 2つの結合は、90度以上開いていないといけない。45度などでは結合はできない。
- 例えば、上と右上は45になってしまうので結合はできない。上と右であれば90度で結合できる。
- 結合が直交してはいけない。×印になるような結合はできない。
- 2つの膜分子同士の結合は、以下の三つの状態に応じて参照される確率が変化する。
- 2つの膜同士が結合を持っていない(最初の結合)の場合 -> PROBABILITY_BONDING_CHAIN_INITIATE を参照する。
- 2つの膜同士が1つずつ結合を持っている場合 -> PROBABILITY_BONDING_CHAIN_SPLICE を参照する。
- その他の場合 -> PROBABILITY_BONDING_CHAIN_EXTEND を参照する。
- ※SPLICEは
継ぎ合わせるなどの意味で設定されています。
- ムーア近傍に触媒分子(C)が存在しないこと。
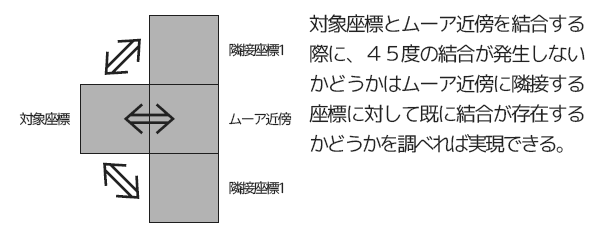
結合する際に、45度の結合になってしまうかどうかは以下のように、事前に実装したget_adjacent_2_moore_neighborhood関数で得られるムーア近傍の2つの隣接座標に対して既に結合していないかどうかを調べることでチェックできます。
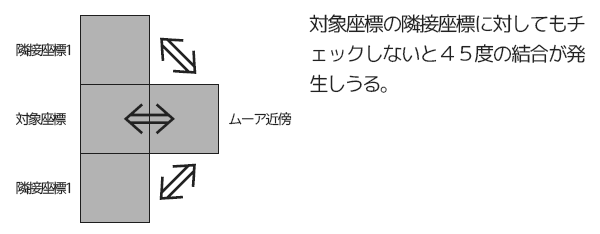
また、ムーア近傍の隣接座標だけではなく、逆に対象座標の隣接座標に対してムーア近傍からの結合が存在しないことを確認しないと、45度の結合が発生してしまうので条件に加えます。
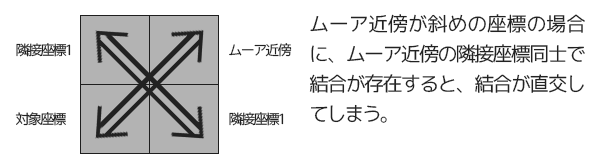
直交判定に関しては、ムーア近傍が斜めの場合にその隣接座標同士で結合がある場合は結合が直交してしまうため、結合できないようにします。
実装に移ります。条件が結構多いので、一部の処理を関数分割しており、複数の関数を利用しています。
def catalyst_exists_in_moore_neighborhoods(particles: np.array, x: int, y: int):
"""
ムーア近傍に触媒分子(C)が存在するかどうかの真偽値を取得する。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
exists : bool
存在する場合はTrueが設定される。
"""
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
for moore_x, moore_y in moore_neighborhood_list:
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_CATALYST:
continue
return True
return False
def get_bonding_probability(particle: Particle, moore_particle: Particle):
"""
対象座標の膜分子とムーア近傍の膜分子の結合状況に応じた対象の
結合の反応確率を取得する。
Parameters
----------
particle : Particle
対象座標の膜分子。
moore_particle : Particle
結合先のムーア近傍の膜分子。
Returns
-------
probability : float
結合状況に応じて算出された必要な反応確率。
"""
if len(particle.bonds) == 0 and len(moore_particle.bonds) == 0:
probability = PROBABILITY_BONDING_CHAIN_INITIATE
elif len(particle.bonds) == 1 and len(moore_particle.bonds) == 1:
probability = PROBABILITY_BONDING_CHAIN_SPLICE
else:
probability = PROBABILITY_BONDING_CHAIN_EXTEND
return probability
def bonding(particles: np.array, x: int, y: int):
"""
膜分子同士の結合処理の反応を実行する。
Notes
-----
条件は関数内のコメントを参照のこと。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
# 対象の座標の分子が膜分子(L)では無い場合は実行しない。
particle: Particle = particles[y, x]
if (particle.type_name != TYPE_NAME_LINK
and particle.type_name != TYPE_NAME_LINK_SUBSTRATE):
return
# ランダムに選択された近傍の分子が膜分子(L)では無い場合は実行しない。
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if (moore_particle.type_name != TYPE_NAME_LINK
and moore_particle.type_name != TYPE_NAME_LINK_SUBSTRATE):
return
# 既に結合先のムーア近傍に対しての結合がされている場合は実行しない。
bond: Bond
for bond in particle.bonds:
if bond.to_x == moore_x and bond.to_y == moore_y:
return
# 既に1つ目もしくは2つ目の膜分子が2つ結合を持っている場合は実行しない。
if len(particle.bonds) == 2 or len(moore_particle.bonds) == 2:
return
# ムーア近傍の隣接座標に対して結合が既に存在する場合は45度の結合になってしまうため
# 実行しない。
adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2 = \
get_adjacent_2_moore_neighborhood(
x=x, y=y, moore_x=moore_x, moore_y=moore_y)
for bond in particle.bonds:
if bond.to_x == adjacent_x_1 and bond.to_y == adjacent_y_1:
return
if bond.to_x == adjacent_x_2 and bond.to_y == adjacent_y_2:
return
# ムーア近傍の隣接座標同士が結合している場合には結合が直交してしまうので実行しない。
adjacent_1_particle: Particle = particles[adjacent_y_1, adjacent_x_1]
for bond in adjacent_1_particle.bonds:
if bond.to_x == adjacent_x_2 and bond.to_y == adjacent_y_2:
return
# ムーア近傍に触媒分子が存在する場合は実行しない。
catalyst_exists = catalyst_exists_in_moore_neighborhoods(
particles=particles, x=x, y=y)
if catalyst_exists:
return
# 対象座標とムーア座標のそれぞれの膜が持っている結合の数次第で発生確率を
# 分岐させる。
probability = get_bonding_probability(
particle=particle, moore_particle=moore_particle)
if not evaluate_probability(probability=probability):
return
# 結合設定を追加する。
particle.bonds.append(Bond(to_x=moore_x, to_y=moore_y))
moore_particle.bonds.append(Bond(to_x=x, to_y=y))
手動で動かして試します。3x3のサイズで、膜分子を配置して、真ん中の座標に対してどのような反応になるのかを見てみます。
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particles[row, column] = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
particles[1, 1].type_name = TYPE_NAME_LINK
moore_neighborhood_list = get_moore_neighborhood_list(x=1, y=1)
for moore_x, moore_y in moore_neighborhood_list:
moore_particle = particles[moore_y, moore_x]
moore_particle.type_name = TYPE_NAME_LINK
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように実行できます。反応確率が絡むので、反応しないときも多いですが何度も実行していると結合が発生してきます。
bonding(particles=particles, x=1, y=1)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
2個までしか結合しないため、これ以上は何度実行しても反応しなくなります。
また、何度かリセットして実行していても、結合角度がちゃんと45度にならないことが確認できます。
結構長くなりましたが、これで反応関係の実装は終わりです・・・!
初期化
反応の実装が終わったので、実際に動かすための初期化設定を進めます。
基質分子の配置
グリッド上の各セルに、 INITIAL_SUBSTRATE_DENSITY の確率で基質分子(S)を配置していきます。
確率を評価してFalseが返ってきたセルに関しては空(HOLE)の設定をします。
INITIAL_SUBSTRATE_DENSITY = 0.8
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
if evaluate_probability(probability=INITIAL_SUBSTRATE_DENSITY):
particle = Particle(
type_name_=TYPE_NAME_SUBSTRATE, is_disintegrated=False, bonds=[])
else:
particle = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
particles[row, column] = particle
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように基質が配置されました。
触媒分子の配置
続いて触媒分子(C)の配置を進めます。
今回は初期値を固定の値で持ち、3つ配置してみました。
class Position:
"""
座標情報を扱うクラス。
Attributes
----------
x : int
x座標。
y : int
y座標。
"""
def __init__(self, x, y):
self.x = x
self.y = y
INITIAL_CATALYST_POSITIONS = [
Position(x=4, y=4), Position(x=8, y=8), Position(x=12, y=12)]
position: Position
for position in INITIAL_CATALYST_POSITIONS:
particle = particles[position.y, position.x]
particle.type_name = TYPE_NAME_CATALYST
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のようになっています。
分子の移動の実装
続いて分子の移動のための実装を進めます。
以下のような形で対応します。
- while文の一度のループで移動できるのは1回のみ。
- 移動済みかどうかは
moved_arr変数で保持し、既にTrueであれば移動しないようにする。 - 移動先はノイマン近傍が対象となる。
- 事前に定義した
MOBILITY_FACTORの設定に応じて、分子の種類ごとに移動確率を算出して評価する。 - 移動先の分子と入れ替える形で移動を行う。そのため、移動先側の分子に対しても移動済みなどのフラグをチェックする。
- 移動済みかどうかは
while True:
# 分子の異動を実行する。
moved_arr = np.full(shape=particles.shape, fill_value=False, dtype=bool)
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
moved: bool = moved_arr[row, column]
particle: Particle = particles[row, column]
neumann_x, neumann_y = get_random_neumann_neighborhood(
x=column, y=row)
neumann_particle: Particle = particles[neumann_y, neumann_x]
neumann_moved: bool = moved_arr[neumann_y, neumann_x]
mobility_factor_probability = np.sqrt(
MOBILITY_FACTOR[particle.type_name]
* MOBILITY_FACTOR[neumann_particle.type_name])
if (not moved
and not neumann_moved
and len(particle.bonds) == 0
and len(neumann_particle.bonds) == 0
and evaluate_probability(
probability=mobility_factor_probability)):
particles[row, column] = neumann_particle
particles[neumann_y, neumann_x] = particle
moved_arr[row, column] = True
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
以下のように動きます。基質は数が多く確率的に頻繁に動くので分かりづらいですが、触媒のほうは隣接座標にゆっくり動いていることが分かります。
最後に、ループで各反応を実行する処理をwhile文の中に追加して完成です。
...
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
production(particles=particles, x=column, y=row)
disintegration(particles=particles, x=column, y=row)
bonding(particles=particles, x=column, y=row)
bond_decay(particles=particles, x=column, y=row)
absorption(particles=particles, x=column, y=row)
emission(particles=particles, x=column, y=row)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
コードは結構ボリュームがありましたが、完成して動くと楽しいですね・・。
最終コード全体
from typing import Dict, List
import numpy as np
from alifebook_lib.visualizers import SCLVisualizer
visualizer = SCLVisualizer()
SPACE_SIZE = 16
TYPE_NAME_SUBSTRATE = 'SUBSTRATE'
TYPE_NAME_CATALYST = 'CATALYST'
TYPE_NAME_LINK = 'LINK'
TYPE_NAME_LINK_SUBSTRATE = 'LINK_SUBSTRATE'
TYPE_NAME_HOLE = 'HOLE'
TYPE_NAME_LIST = [
TYPE_NAME_SUBSTRATE,
TYPE_NAME_CATALYST,
TYPE_NAME_LINK,
TYPE_NAME_LINK_SUBSTRATE,
TYPE_NAME_HOLE,
]
class Bond:
"""
膜分子の結合情報単体を扱うクラス。
Attributes
----------
to_x : int
結合先のX座標。
to_y : int
結合先のY座標。
"""
def __init__(self, to_x: int, to_y: int):
self.to_x = to_x
self.to_y = to_y
class Particle:
"""
分子1つ分のオブジェクトを生成するクラス。
Attributes
----------
type_name : str
分子の種別値名。
is_disintegrated : bool
崩壊済みかどうか。膜分子のみ設定される。もしTrueの場合、
基質(S)分子が放出可能(近傍に空いているグリッドが2つ
存在する等)な場合に膜分子から基質への変化が実行される。
もし放出が出来ない条件(近傍に空いているグリッドが存在
しない等)の場合には、この真偽値は引き継がれ、次回の
タイミングで放出可能かどうかがチェックされる。
bonds : list of Bonds
膜の結合先の情報を格納したリスト。
"""
def __init__(
self, type_name_: str, is_disintegrated: bool, bonds: list):
self.type_name: str = type_name_
self.is_disintegrated: bool = is_disintegrated
self.bonds: List[Bond] = bonds
@property
def type_name(self) -> str:
return self._type_name
@type_name.setter
def type_name(self, value: str):
"""
種別値名。
Parameters
----------
value : str
設定する種別値名。
Raises
------
ValueError
定義されていない種別値が指定された場合。
"""
is_in = value in TYPE_NAME_LIST
if not is_in:
err_msg = '定義されていない種別値が指定されています : %s' \
% value
raise ValueError(err_msg)
self._type_name = value
def to_visualizer_bonds(bonds: list) -> list:
"""
可視化で必要なフォーマットに、膜(L)の連結情報のリストを
変換する。
Parameters
----------
bonds : list of bond
変換対象のリスト。
Returns
-------
visualizer_bonds : list of dicts
可視化用のフォーマットに変換された連結情報のリスト。
"""
visualizer_bonds = []
bond: Bond
for bond in bonds:
bond_tuple = (bond.to_y, bond.to_x)
visualizer_bonds.append(bond_tuple)
return visualizer_bonds
def to_visualizer_arr_from_particles(particles: np.array) -> np.array:
"""
分子の行列のデータを、可視化で必要なフォーマットに変換する。
Parameters
----------
particles : np.array
変換対象の分子のオブジェクトを格納した2次元配列。
Returns
-------
visualiser_arr : np.array
変換された可視化用の配列。
"""
visualiser_arr = np.empty(shape=(SPACE_SIZE, SPACE_SIZE), dtype=object)
particle: Particle
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
particle = particles[row, column]
visualiser_arr[row, column] = {
'type': particle.type_name,
'disintegrating_flag': particle.is_disintegrated,
'bonds': to_visualizer_bonds(bonds=particle.bonds),
}
return visualiser_arr
def get_neumann_neighborhood_list(x, y):
"""
指定された座標のノイマン近傍の4つの座標を格納したリストを取得する。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
neumann_neighborhood_list : list of tuple
ノイマン近傍の4つの座標を格納したリスト。右・左・下・上の順番で
格納される。
"""
neumann_neighborhood_list = [
((x + 1) % SPACE_SIZE, y),
((x - 1) % SPACE_SIZE, y),
(x, (y + 1) % SPACE_SIZE),
(x, (y - 1) % SPACE_SIZE),
]
return neumann_neighborhood_list
def get_random_neumann_neighborhood(x, y):
"""
指定された座標のノイマン近傍のうち、ランダムに1つの座標を返す。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
neumann_x : int
算出されたノイマン近傍のx座標。
neumann_y : int
算出されたノイマン近傍のy座標。
"""
neumann_neighborhood_list = get_neumann_neighborhood_list(x=x, y=y)
random_index = np.random.randint(
low=0,
high=len(neumann_neighborhood_list))
neumann_x = neumann_neighborhood_list[random_index][0]
neumann_y = neumann_neighborhood_list[random_index][1]
return neumann_x, neumann_y
def get_moore_neighborhood_list(x, y):
"""
指定された座標のムーア近傍の8つの座標を格納したリストを取得する。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_neighborhood_list : list of tuple
ムーア近傍の8つの座標を格納したリスト。左上・上・右上・左・中央・右・
左下・下・右下の順番に格納される。
"""
left_x = (x - 1) % SPACE_SIZE
right_x = (x + 1) % SPACE_SIZE
upper_y = (y - 1) % SPACE_SIZE
lower_y = (y + 1) % SPACE_SIZE
moore_neighborhood_list = [
(left_x, upper_y),
(x, upper_y),
(right_x, upper_y),
(left_x, y),
(right_x, y),
(left_x, lower_y),
(x, lower_y),
(right_x, lower_y),
]
return moore_neighborhood_list
def get_random_moore_neighborhood(x, y):
"""
指定された座標のムーア近傍のうち、ランダムに1つの座標を返す。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_x : int
算出されたムーア近傍のx座標。
moore_y : int
算出されたムーア近傍のy座標。
"""
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
random_index = np.random.randint(
low=0, high=len(moore_neighborhood_list))
moore_x = moore_neighborhood_list[random_index][0]
moore_y = moore_neighborhood_list[random_index][1]
return moore_x, moore_y
def get_random_2_moore_neighborhood(x, y):
"""
指定された座標のムーア近傍のうち、ランダムに2つの座標を取得する。
2つの近傍の座標はそれぞれ隣接している座標の中から算出される。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
moore_x_1 : int
1つ目のムーア近傍のx座標。
moore_y_1 : int
1つ目のムーア近傍のy座標。
moore_x_2 : int
2つ目のムーア近傍のx座標。
moore_y_2 : int
2つ目のムーア近傍のy座標。
"""
moore_x_1, moore_y_1 = get_random_moore_neighborhood(x=x, y=y)
if x == moore_x_1:
moore_x_2 = np.random.choice([
(moore_x_1 - 1) % SPACE_SIZE,
(moore_x_1 + 1) % SPACE_SIZE,
])
moore_y_2 = moore_y_1
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
if y == moore_y_1:
moore_x_2 = moore_x_1
moore_y_2 = np.random.choice([
(moore_y_1 - 1) % SPACE_SIZE,
(moore_y_1 + 1) % SPACE_SIZE,
])
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
choice = [(x, moore_y_1), (moore_x_1, y)]
random_index = np.random.randint(0, 2)
moore_x_2, moore_y_2 = choice[random_index]
return moore_x_1, moore_y_1, moore_x_2, moore_y_2
def get_adjacent_2_moore_neighborhood(x, y, moore_x, moore_y):
"""
指定された対象座標とそのムーア近傍に隣接した2つの座標を取得する。
返却される2つの座標は、指定された座標のムーア近傍が設定される。
Parameters
----------
x : int
対象のx座標。
y : int
対象のy座標。
moore_x : int
対象座標のムーア近傍のx座標。
moore_y : int
対象座標のムーア近傍のy座標。
Returns
-------
adjacent_x_1 : int
算出された1つ目のムーア近傍に隣接したx座標。
adjacent_y_1 : int
算出された1つ目のムーア近傍に隣接したy座標。
adjacent_x_2 : int
算出された2つ目のムーア近傍に隣接したx座標。
adjacent_y_2 : int
算出された2つ目のムーア近傍に隣接したy座標。
"""
if x == moore_x:
adjacent_x_1 = (moore_x - 1) % SPACE_SIZE
adjacent_y_1 = moore_y
adjacent_x_2 = (moore_x + 1) % SPACE_SIZE
adjacent_y_2 = moore_y
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
if y == moore_y:
adjacent_x_1 = moore_x
adjacent_y_1 = (moore_y - 1) % SPACE_SIZE
adjacent_x_2 = moore_x
adjacent_y_2 = (moore_y + 1) % SPACE_SIZE
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
adjacent_x_1 = x
adjacent_y_1 = moore_y
adjacent_x_2 = moore_x
adjacent_y_2 = y
return adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2
MOBILITY_FACTOR: Dict[str, float] = {
TYPE_NAME_HOLE: 0.1,
TYPE_NAME_SUBSTRATE: 0.1,
TYPE_NAME_CATALYST: 0.0001,
TYPE_NAME_LINK: 0.05,
TYPE_NAME_LINK_SUBSTRATE: 0.05,
}
PROBABILITY_PRODUCTION = 0.95
PROBABILITY_DISINTEGRATION = 0.0005
PROBABILITY_BONDING_CHAIN_INITIATE = 0.3
PROBABILITY_BONDING_CHAIN_EXTEND = 0.3
PROBABILITY_BONDING_CHAIN_SPLICE = 0.9
PROBABILITY_BOND_DECAY = 0.0005
PROBABILITY_ABSORPTION = 0.5
PROBABILITY_EMISSION = 0.5
def evaluate_probability(probability: float) -> bool:
"""
確率probabilityに応じて、TrueもしくはFalseを返す。
Parameters
----------
probability : float
評価対象の確率。
Returns
-------
bool
確率に応じた真偽値が設定される。
"""
return np.random.rand() < probability
true_num = 0
false_num = 0
for i in range(100000):
if evaluate_probability(probability=0.8):
true_num += 1
else:
false_num += 1
def production(particles: np.array, x: int, y: int):
"""
条件を満たした場合に、2つの基質分子(S)を1つの膜分子(L)に
変化させる。以下の条件で判定が実行される。
- 指定された座標の分子が触媒分子(C)であること。
- 指定された座標のランダムなムーア近傍を2つ選択し、それらの座標が
基質分子であること。
- ※2つのムーア近傍は隣接している必要がある。
- production発生確率を評価し、Trueが返却されること。
変化後として、以下のような変化が設定される。
- 1つ目のムーア近傍の座標は空(HOLE)になる。
- 2つ目のムーア近傍の座標は膜(L)になる。
Parameters
----------
particles : array-like
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_CATALYST:
return
moore_x_1, moore_y_1, moore_x_2, moore_y_2 = \
get_random_2_moore_neighborhood(x=x, y=y)
moore_particle_1: Particle = particles[moore_y_1, moore_x_1]
if moore_particle_1.type_name != TYPE_NAME_SUBSTRATE:
return
moore_particle_2: Particle = particles[moore_y_2, moore_x_2]
if moore_particle_2.type_name != TYPE_NAME_SUBSTRATE:
return
if not evaluate_probability(probability=PROBABILITY_PRODUCTION):
return
moore_particle_1.type_name = TYPE_NAME_HOLE
moore_particle_2.type_name = TYPE_NAME_LINK
def emission(
particles: np.array, x: int, y: int,
probability: float=PROBABILITY_EMISSION):
"""
基質(S)を吸収した膜分子(LINK_SUBSTRATE)で、基質を放出する
反応を実行する。以下の条件を満たした場合に実行される。
- 対象の座標の分子が基質(S)を吸収した膜分子(LINK_SUBSTRATE)
であること。
- ランダムに選択したムーア近傍が、空(HOLE)であること。
- 指定された確率を評価して、Trueが返ること。
変化後として、以下のような変化が設定される。
- LINK_SUBSTRATE から膜(LINK)に変化する。
- 空(HOLE)の近傍座標は基質(S)に変化する。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_LINK_SUBSTRATE:
return
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_HOLE:
return
if not evaluate_probability(probability=probability):
return
particle.type_name = TYPE_NAME_LINK
moore_particle.type_name = TYPE_NAME_SUBSTRATE
def bond_decay(
particles: np.array, x: int, y: int,
probability: float=PROBABILITY_BOND_DECAY):
"""
膜分子(L)同士の結合を一定確率で消滅させる。以下の条件を満たす
場合に実行される。
- 対象座標の分子が膜(L)もしくは基質を吸収した膜(LINK_SUBSTRATE)
である。
- 与えられた確率を評価し、Trueが返ること。
変化後として、対象座標に設定されている結合設定(bonds)が空になる。
結合先の結合設定も同様に削除される。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
probability : float, default PROBABILITY_BOND_DECAY
反応の発生確率。
"""
particle: Particle = particles[y, x]
if particle.type_name not in (TYPE_NAME_LINK, TYPE_NAME_SUBSTRATE):
return
if not evaluate_probability(probability=probability):
return
bond: Bond
for bond in particle.bonds:
neighbor_particle: Particle = particles[bond.to_y, bond.to_x]
neighbor_bond: Bond
for neighbor_bond in neighbor_particle.bonds:
if neighbor_bond.to_x != x or neighbor_bond.to_y != y:
continue
# 結合先の膜分子側の結合情報を削除する。
neighbor_particle.bonds.remove(neighbor_bond)
break
particle.bonds = []
def disintegration(particles, x, y):
"""
膜分子(L)から2つの基質分子(S)に変化する反応を実行する。
以下の条件を満たした場合に実行される。
- 対象の座標が膜分子(L)もしくは基質を吸収した膜分子
(LINK_SUBSTRATE)である。
- 確率評価の結果Trueが返却された。
- 基質を吸収している場合には、放出済みである。
- ランダムに選択したムーア近傍の座標が空(HOLE)である。
変化後として、以下のような変化が設定される。
- 基質分子を吸収している場合には放出される(emission)。
- 対象座標は基質分子となり、ムーア近傍にも1つ基質分子が発生する。
- 結合している場合には結合は解除される(bond_decay)。
Notes
-----
基質の放出や2つの基質への変化の都合、条件によっては即時で
反応を発生させることができないケースがある(近傍が埋まっていて
放出ができない場合など)。
そのような場合には、反応が実施されるフラグ(is_disintegrated)
はTrueのままなので、繰り返し反応が完了するまで実行される。
(一度確率を評価してフラグがTrueになった場合は、その後は反応が
起きるまでずっと反応が試みられる)
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name in (TYPE_NAME_LINK, TYPE_NAME_LINK_SUBSTRATE):
if evaluate_probability(probability=PROBABILITY_DISINTEGRATION):
particle.is_disintegrated = True
if not particle.is_disintegrated:
return
# 基質分子を吸収している場合には放出する。
emission(particles=particles, x=x, y=y, probability=1.0)
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
# 基質の放出などが完了していない場合などには処理を行わない。
if particle.type_name != TYPE_NAME_LINK:
return
if moore_particle.type_name != TYPE_NAME_HOLE:
return
bond_decay(particles=particles, x=x, y=y, probability=1.0)
particle.type_name = TYPE_NAME_SUBSTRATE
moore_particle.type_name = TYPE_NAME_SUBSTRATE
particle.is_disintegrated = False
def absorption(particles: np.array, x: int, y: int):
"""
膜分子(L)が近傍に存在する基質分子(S)を吸収し、LINK_SUBSTRATE
に変化する反応を実行する。以下の条件を満たす場合に実行される。
- 対象座標が膜分子であること。
- ランダムに選択したムーア近傍の座標が、基質分子であること。
- 確率を評価してTrueが返ること。
変化後として、以下のような変化が設定される。
- 膜分子(L)はLINK_SUBSTRATEになる。
- 基質分子(S)は空(HOLE)になる。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
particle: Particle = particles[y, x]
if particle.type_name != TYPE_NAME_LINK:
return
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_SUBSTRATE:
return
if not evaluate_probability(probability=PROBABILITY_ABSORPTION):
return
particle.type_name = TYPE_NAME_LINK_SUBSTRATE
moore_particle.type_name = TYPE_NAME_HOLE
def catalyst_exists_in_moore_neighborhoods(particles: np.array, x: int, y: int):
"""
ムーア近傍に触媒分子(C)が存在するかどうかの真偽値を取得する。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
Returns
-------
exists : bool
存在する場合はTrueが設定される。
"""
moore_neighborhood_list = get_moore_neighborhood_list(x=x, y=y)
for moore_x, moore_y in moore_neighborhood_list:
moore_particle: Particle = particles[moore_y, moore_x]
if moore_particle.type_name != TYPE_NAME_CATALYST:
continue
return True
return False
def get_bonding_probability(particle: Particle, moore_particle: Particle):
"""
対象座標の膜分子とムーア近傍の膜分子の結合状況に応じた対象の
結合の反応確率を取得する。
Parameters
----------
particle : Particle
対象座標の膜分子。
moore_particle : Particle
結合先のムーア近傍の膜分子。
Returns
-------
probability : float
結合状況に応じて算出された必要な反応確率。
"""
if len(particle.bonds) == 0 and len(moore_particle.bonds) == 0:
probability = PROBABILITY_BONDING_CHAIN_INITIATE
elif len(particle.bonds) == 1 and len(moore_particle.bonds) == 1:
probability = PROBABILITY_BONDING_CHAIN_SPLICE
else:
probability = PROBABILITY_BONDING_CHAIN_EXTEND
return probability
def bonding(particles: np.array, x: int, y: int):
"""
膜分子同士の結合処理の反応を実行する。
Notes
-----
条件は関数内のコメントを参照のこと。
Parameters
----------
particles : array-like, default PROBABILITY_EMISSION
グリッドの各分子を格納した2次元配列。
x : int
対象のx座標。
y : int
対象のy座標。
"""
# 対象の座標の分子が膜分子(L)では無い場合は実行しない。
particle: Particle = particles[y, x]
if (particle.type_name != TYPE_NAME_LINK
and particle.type_name != TYPE_NAME_LINK_SUBSTRATE):
return
# ランダムに選択された近傍の分子が膜分子(L)では無い場合は実行しない。
moore_x, moore_y = get_random_moore_neighborhood(x=x, y=y)
moore_particle: Particle = particles[moore_y, moore_x]
if (moore_particle.type_name != TYPE_NAME_LINK
and moore_particle.type_name != TYPE_NAME_LINK_SUBSTRATE):
return
# 既に結合先のムーア近傍に対しての結合がされている場合は実行しない。
bond: Bond
for bond in particle.bonds:
if bond.to_x == moore_x and bond.to_y == moore_y:
return
# 既に1つ目もしくは2つ目の膜分子が2つ結合を持っている場合は実行しない。
if len(particle.bonds) == 2 or len(moore_particle.bonds) == 2:
return
# ムーア近傍の隣接座標に対して結合が既に存在する場合は45度の結合になってしまうため
# 実行しない。
adjacent_x_1, adjacent_y_1, adjacent_x_2, adjacent_y_2 = \
get_adjacent_2_moore_neighborhood(
x=x, y=y, moore_x=moore_x, moore_y=moore_y)
for bond in particle.bonds:
if bond.to_x == adjacent_x_1 and bond.to_y == adjacent_y_1:
return
if bond.to_x == adjacent_x_2 and bond.to_y == adjacent_y_2:
return
# ムーア近傍の隣接座標同士が結合している場合には結合が直交してしまうので実行しない。
adjacent_1_particle: Particle = particles[adjacent_y_1, adjacent_x_1]
for bond in adjacent_1_particle.bonds:
if bond.to_x == adjacent_x_2 and bond.to_y == adjacent_y_2:
return
# ムーア近傍に触媒分子が存在する場合は実行しない。
catalyst_exists = catalyst_exists_in_moore_neighborhoods(
particles=particles, x=x, y=y)
if catalyst_exists:
return
# 対象座標とムーア座標のそれぞれの膜が持っている結合の数次第で発生確率を
# 分岐させる。
probability = get_bonding_probability(
particle=particle, moore_particle=moore_particle)
if not evaluate_probability(probability=probability):
return
# 結合設定を追加する。
particle.bonds.append(Bond(to_x=moore_x, to_y=moore_y))
moore_particle.bonds.append(Bond(to_x=x, to_y=y))
INITIAL_SUBSTRATE_DENSITY = 0.8
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
if evaluate_probability(probability=INITIAL_SUBSTRATE_DENSITY):
particle = Particle(
type_name_=TYPE_NAME_SUBSTRATE, is_disintegrated=False, bonds=[])
else:
particle = Particle(
type_name_=TYPE_NAME_HOLE, is_disintegrated=False, bonds=[])
particles[row, column] = particle
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
class Position:
"""
座標情報を扱うクラス。
Attributes
----------
x : int
x座標。
y : int
y座標。
"""
def __init__(self, x, y):
self.x = x
self.y = y
position: Position
for position in INITIAL_CATALYST_POSITIONS:
particle = particles[position.y, position.x]
particle.type_name = TYPE_NAME_CATALYST
while True:
# 分子の異動を実行する。
moved_arr = np.full(shape=particles.shape, fill_value=False, dtype=bool)
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
moved: bool = moved_arr[row, column]
particle: Particle = particles[row, column]
neumann_x, neumann_y = get_random_neumann_neighborhood(
x=column, y=row)
neumann_particle: Particle = particles[neumann_y, neumann_x]
neumann_moved: bool = moved_arr[neumann_y, neumann_x]
mobility_factor_probability = np.sqrt(
MOBILITY_FACTOR[particle.type_name]
* MOBILITY_FACTOR[neumann_particle.type_name])
if (not moved
and not neumann_moved
and len(particle.bonds) == 0
and len(neumann_particle.bonds) == 0
and evaluate_probability(
probability=mobility_factor_probability)):
particles[row, column] = neumann_particle
particles[neumann_y, neumann_x] = particle
moved_arr[row, column] = True
for row in range(SPACE_SIZE):
for column in range(SPACE_SIZE):
production(particles=particles, x=column, y=row)
disintegration(particles=particles, x=column, y=row)
bonding(particles=particles, x=column, y=row)
bond_decay(particles=particles, x=column, y=row)
absorption(particles=particles, x=column, y=row)
emission(particles=particles, x=column, y=row)
visualizer.update(
particle_data=to_visualizer_arr_from_particles(particles=particles))
余談
今回、JupyterLabに本格的に移行してみて、jupyterlab-lspの補完を使いつつ、且つPythonの型のアノテーションなどもはじめてしっかり使ってみましたが、補完やリアルタイムのLintをしてくれるおかげで、過程のうっかりミスなどが大分減ったような気がします。やはり型は偉大ですね・・・
特に、今までJupyterで関数内とかでよく些細なミスをしたりしていましたが、それらが軽減されて大分良い感じです。