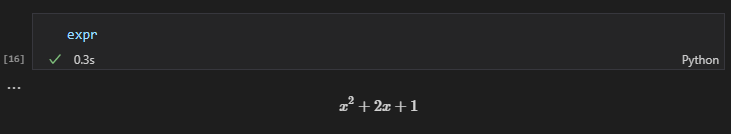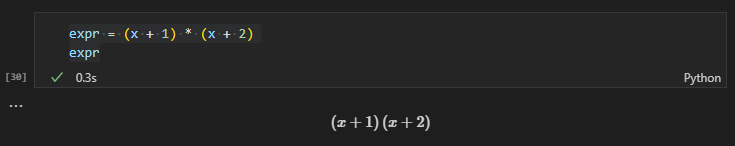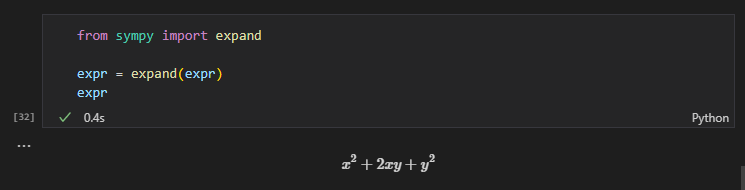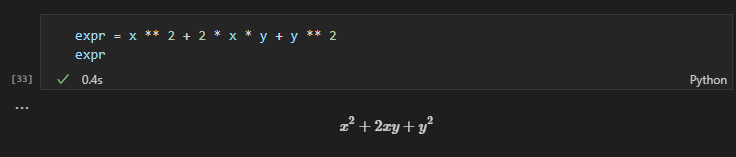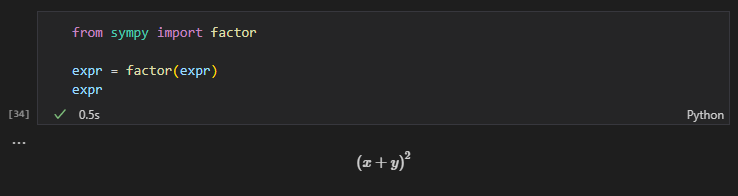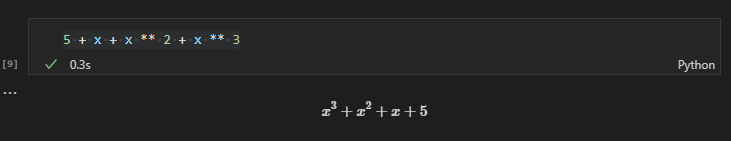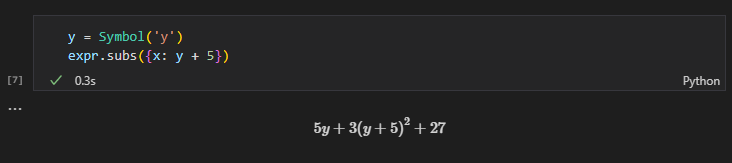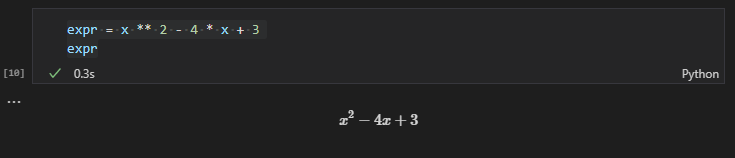数式操作で便利なSymPyの入門

数式表現や操作・可視化などで便利なSymPyライブラリについて入門していくための記事です。

※記事執筆者は理系出身ではなく数学や用語などで色々粗い点等はご容赦ください。

SymPyでできること

以下一例です。後々の節で順番に触れていきます。

• Python上での数式表示が楽になります。
• Python上での数式表現や演算がやりやすくなります。
• ダイレクトに数式を使った計算を行うことができます。
• 数式の解を求めることができます。
• 数式のプロットを行うことができます（内部ではmatplotlibが使われます）。

使うもの

• Windows 10
• Python 3.9.0
• sympy==1.9
• Jupyter（VS Code上のものを利用しているため背景などが黒くなっています）

SymPyのインストール

pipで対応することができます。

$ pip install sympy

※今回は記事執筆時点で最新の1.9のバージョンを使っているため合わせる場合には以下のようなコマンドをお使いください。

$ pip install sympy==1.9

シンボルの定義

$x$や$y$、$a$といったようなアルファベットのシンボルを定義するにはSymPyのシンボルクラスを使います。第一引数にはシンボルに設定するアルファベットを指定します。基本的に変数名と同じ名前を設定します。

例えば$x$というシンボルを定義したい場合には以下のように書きます。

from sympy import Symbol

x: Symbol = Symbol('x')

生成したシンボルをそのままJupyter上で表示すると数式表示のアウトプットになります。少し分かりづらいですがアウトプットでセンタリングされる形で$x$と表示されています。

x

もしくはsymbols関数でまとめてシンボルを定義することもできます。引数にコンマ区切りで各シンボル名を指定します。ただしこちらの場合は現状Pylance（Pyright）などでの型チェックに引っかかります。動作上は問題無く動作します。

from sympy import symbols
x, y = symbols('x, y')

シンボルに対する演算

基本的な演算処理を行う各オペレーターは直接シンボルに対して行うことができます。例えば以下のように2乗や乗算、加算などを行うことができます。

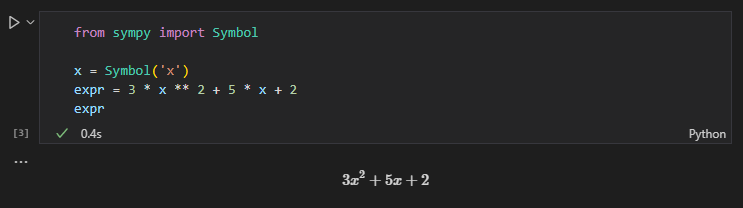
expr = x ** 2 + 2 * x + 1

演算結果はJupyter上で表示してみると数式としてちゃんと反映されていることを確認できます。

expr

括弧などを付けてもちゃんと数式に反映されます。

expr = (x + 1) * (x + 2)
expr

シンボル名の取得や表示

シンボル名を文字列として取得したり表示したい場合にはいくつか方法があります。

1つ目としてはname属性にアクセスする方法です。

name: str = x.name
print('name:', name, '\ntype:', type(name))

name: x
type: <class 'str'>

2つ目としてstr型にキャストする方法も使えます。こちらもそのままシンボル名の文字列になります。

name: str = str(x)
print('name:', name, '\ntype:', type(name))

name: x
type: <class 'str'>

また、print関数にそのまま通してもシンボル名が表示されます。

print(x)

x

数式の展開

expand関数で数式の展開を行うことができます。

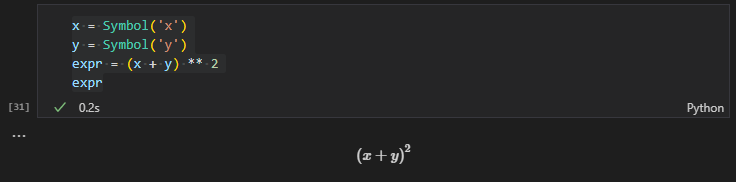
例として$(x + y)^2$という式を展開してみます。まずは対象の式を用意します。

x = Symbol('x')
y = Symbol('y')
expr = (x + y) ** 2
expr

この式をexpand関数を使って展開してみます。

from sympy import expand

expr = expand(expr)
expr

$x^2 + 2xy + y^2$というように展開してくれました。

数式の因数分解

今度は展開とは逆に因数分解してみます。factor関数で扱うことができます。

先ほどの$x^2 + 2xy + y^2$という式をまずは用意します。

expr = x ** 2 + 2 * x * y + y ** 2
expr

factor関数を通してみます。

from sympy import factor

expr = factor(expr)
expr

展開前の式に戻すことができました。

式の自動の計算の挙動

SymPyではシンプルな表現部分は自動で計算され統合などがされます。例えば以下のように$x + x$というシンプルな式であれば$2x$という表示になります。

x + x

一方で式が複雑になってくると計算を行わずにそのまま扱った方が良いケースなども多くなってきます。そういった計算はそのまま残る形となります（全て展開されるわけではありません）。

例えば以下の式では$x + x$の部分が$2x$、$2 * x$の部分が$2x$という形になっていますが、一方で結果は$2x(2x + 1)$となり全て計算されているわけではありません。

(x + x) * (2 * x + 1)

式の要素の表示順

デフォルトではSymPyでの表示は指数の値が大きい方が左側に表示されます。例えば以下のようにPython上で書くとPython上の記述と反対の順番で式が表示されます。

5 + x + x ** 2 + x ** 3

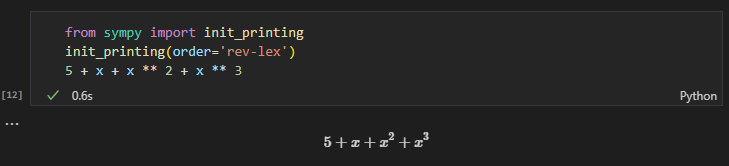
通常は式の表示としてはこれが自然ですが、何らかの理由で逆順に表示したい場合はinit_printing関数でorder='rev-lex'と指定します。rev-lexはreverse lexicographical order （辞書的に逆順）の略となります。この辺は詳しくは触れませんが必要な方は以下のWikipediaの記事などをご確認ください。

from sympy import init_printing
init_printing(order='rev-lex')
5 + x + x ** 2 + x ** 3

ターミナルやコマンドプロンプト上などでも見栄え良く表示したい場合には・・・

Jupyter上などで扱っているとTeXで表示してくれるため特に意識しなくとも良い感じに表示してくれます。一方でターミナルやコマンドプロンプト上での表示が必要な場合にはこの表示は使えません。このようなケースでもある程度読みやすくするためのSymPyのpprint関数が用意されています。

例えば以下のような数式で考えてみます。

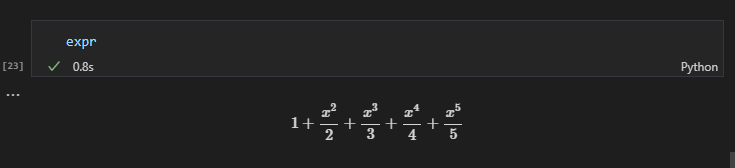
expr = 1 + x ** 2 / 2 + x ** 3 / 3 + x ** 4 / 4 + x ** 5 / 5

Jupyter上で表示してみると以下のように表示されます。

expr

ターミナル上で表示したり、もしくはJupyter上などでprintで表示すると以下のようにテキストで表示されます。ちょっと読みやすい・・・とは言い難い表示となります。

print(expr)

x**5/5 + x**4/4 + x**3/3 + x**2/2 + 1

こういった場合にはSymPyのpprint（pretty-print）を使うと改行やスペースなどが良い感じに入って先ほどのものよりも読みやすい表示になります（指数部分などが小さくなったりは流石に無理ですが・・・）。

from sympy import pprint

pprint(expr)

     2    3    4    5
    x    x    x    x 
1 + ── + ── + ── + ──
    2    3    4    5 

各シンボルに代入を行う

※init_printingの設定をリセットするため一旦Jupyterのカーネルを再起動しています。

式表現のオブジェクトはsubsメソッドを持っているため、そちらに値を指定することで各シンボルに代入を行うことができます（substitutionで代入という意味になります）。

例えば以下のような式で考えてみます。

from sympy import Symbol

x = Symbol('x')
expr = 3 * x ** 2 + 5 * x + 2
expr

この式に対してsubsメソッドでx = 6という値を代入してみましょう。辞書の形でキーに対象のシンボル、値に代入したい値を指定して使います。

expr.subs({x: 6})

3 * 6 ** 2 + 5 * 6 + 2で140という値を得ることができました。

この代入処理は別のシンボルを含めることもできます。例えばx = y + 5という条件だった場合、そのまま辞書の値にy + 5という値を指定することができます。

y = Symbol('y')
expr.subs({x: y + 5})

文字列からSymPyのオブジェクトへ変換する

DBへ保存したりユーザーからの入力値を受け付ける場合などには値がSymPyの数式のオブジェクトではなく数式表現用の文字列になります。これらの文字列をSymPyのオブジェクトへ変換したり戻したりしたい場合にはsympifyという関数が用意されておりそちらを使うことで実現できます。

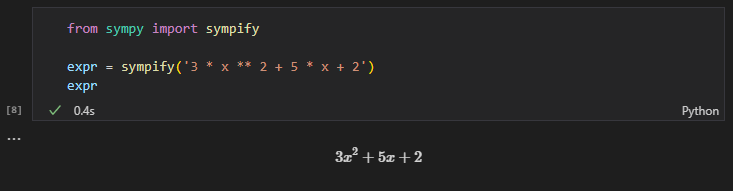
from sympy import sympify

expr = sympify('3 * x ** 2 + 5 * x + 2')
expr

文字列から変換できない場合（不正な数式表現の文字列の場合）などにはエラーになります。

例えば以下のように文字列上では3 * xと*を挟まないといけない箇所で3xなどとなっていた場合などにはエラーになります。

expr = sympify('3x')

SympifyError: Sympify of expression 'could not parse '3x'' failed, because of exception being raised:
SyntaxError: invalid syntax (<string>, line 1)

式の解を求める

式でどんな値を設定すると0になるか・・・といった解を求めることがsolve関数を使って行うことができます。

例えば$x^2 - 4x + 3 = 0$という二次方程式の解を考えてみます。

まずは数式を用意します。

expr = x ** 2 - 4 * x + 3
expr

そちらを使ってsolve関数を通してみます。

from sympy import solve
solve(expr)

[1, 3]

1と3という解が得られました。なお今回使った2次方程式では解が2つですが、解が1つの式の場合でも結果はリストで返ってきます。

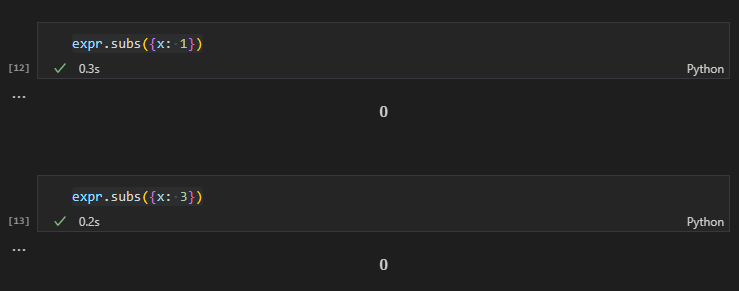
試しに得られた1と3の解をsubsメソッドで代入して結果が0になることを確認してみます。

expr.subs({x: 1})

expr.subs({x: 3})

それぞれの解を代入すると結果が0になることを確認することができました。

数式をプロットする

SymPyでは内部でmatplotlibを使う形でプロットするインターフェイスが用意されているため、数式をダイレクトにプロットすることができます。

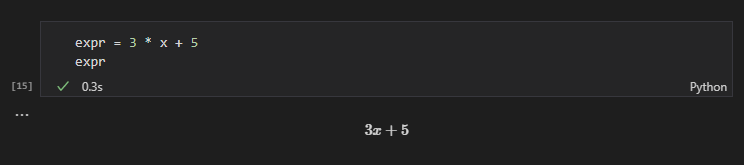
例として$y = 3x + 5$という一次関数の式を使ってみます。

expr = 3 * x + 5
expr

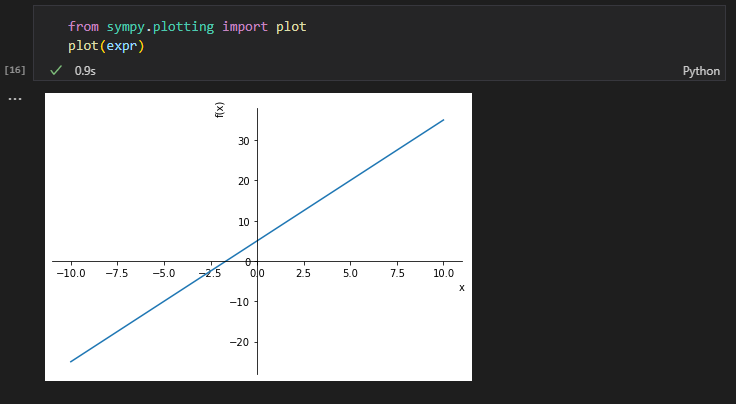
プロットのインターフェイスはsympy.plottingパッケージにplot関数が含まれているのでそちらを使います。

from sympy.plotting import plot
plot(expr)

可視化までがお手軽ですね。

横軸の範囲を調整する

plot関数は前節で可視化された結果の通り、デフォルトでは横軸（前節ではxの値）は-10～10の範囲で設定されます。

この範囲を変えたい場合にはplot関数の引数に2件の引数を指定します。第一引数には対象の数式、第二引数には対象のシンボル・横軸最小値・横軸最大値の3つの値を格納したタプルを指定します。

たとえば-5～5の範囲にしたければ以下のように書きます。

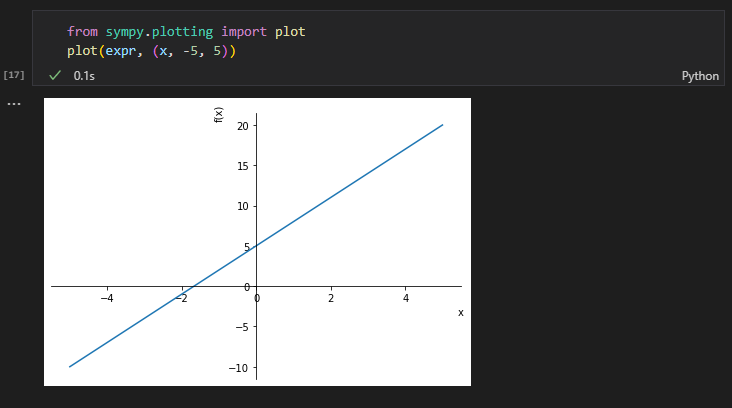
from sympy.plotting import plot
plot(expr, (x, -5, 5))

タイトルや軸のラベルなどを設定する

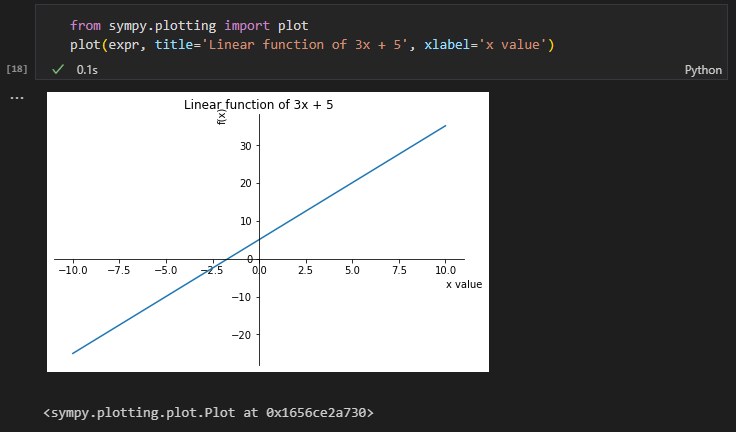
plot関数にはtitle, xlabel, ylabelといったmatplotlibでお馴染みの引数があるため、それらをキーワード引数で指定することもできます。

from sympy.plotting import plot
plot(expr, title='Linear function of 3x + 5', xlabel='x value')

複数の数式を同時に表示する

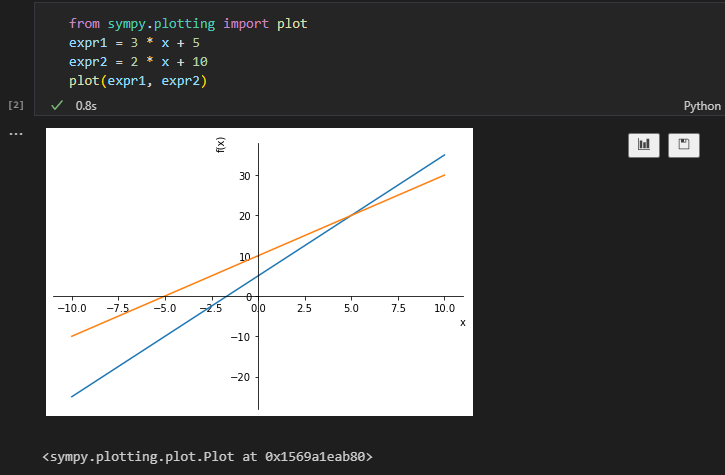
複数の数式を同時にプロットしたい場合には第一引数に1つ目の数式のオブジェクト、第二引数に2つ目の数式のオブジェクト・・・と順番に指定していくことで対応できます。

from sympy.plotting import plot
expr1 = 3 * x + 5
expr2 = 2 * x + 10
plot(expr1, expr2)

参考文献・参考サイトまとめ