LoginSignup
11
5
この記事誰得？ 私しか得しないニッチな技術で記事投稿！
@sikeda

互除法よりも高速な (こともある) 最大公約数アルゴリズム

Last updated at Posted at 2023-06-30

最大公約数とは

最大公約数 (GCD) とは、2つ以上の整数のすべての公約数を約数に持つ公約数のことです。$$\tag{0}$$

単に「公約数の中で最大のもの」と定義しないのは、次のようなコーナーケースもカバーしたいからですね。

  • 負の数も含めると、「最大」の意味が不明になる。
  • ゼロも含めて「$0$と$0$の最大公約数」も考えたいが、$0$には何を掛けても$0$になるので「最大のもの」が決まらない。
  • 「$0$と$0$以外の最大公約数」も考えたいが以下同文。

$(0)$ の定義なら、負の数の最大公約数も決まりますし、「$0$と$0$の最大公約数」は$0$、「$0$と$0$以外の最大公約数」は$0$以外のほうの数、ということになります。

当記事で、${\rm GCD}(m, n)$ は整数 $m$ と $n$ との最大公約数を表すものとします。なお、次のことは明らかです。

{\rm GCD}(m, n) = {\rm GCD}(n, m) \tag{1}

{\rm GCD}(m, n) = {\rm GCD}(\pm m, \pm n) \tag{2}

以降では、2つの整数が与えられたときにそれらの最大公約数を求めるためのアルゴリズムについて書きます。

互除法

古くから知られている最大公約数を求めるためのアルゴリズムとして「互除法」があります。たとえば、紀元前3世紀ころのアレクサンドリアのエウクレイデスによる『原論』(Στοιχεῖα) という書物にはつぎの記述があります。

命題一 二つの不等な数が定められ、常に大きい数から小さい数が引き去られるとき、もし単位1が残されるまで、残された数が自分の前の数を割り切らないならば、最初の二数は互いに素であろう。

命題二 互いに素でない二数が与えられたとき、それらの最大公約数を見いだすこと。

系 もしある数が二つの数を割り切るならば、それらの最大公約数をも割り切るであろう。2

つまり、大きいほうの数から小さいほうの数を引くことを繰り返して、最後に$1$が残れば二数は互いに素 (最大公約数は$1$)、そうではなく何も残らなければ二数の最大公約数は直前に残っていた数、ということになります。これは、次の関係によります。

{\rm GCD}(m, n) = {\rm GCD}(m - n, n) = {\rm GCD}(n, m - n)\tag{3}

これをそのままコーディングすれば、次のようになるでしょう3。

func GCD_Euclidean(m, n uint) uint {
	if m == 0 {
		return n
	}
	if n == 0 {
		return m
	}

	for {
		if m == 1 || n == 1 {
			return 1
		}
		switch {
		case m > n:
			m -= n
		case m < n:
			n -= m
		default:
			return m
		}
	}
}

m、nは単調減少するため、このアルゴリズムは必ず停止し、最後に最大公約数が得られます。

減算を繰り返すため、手計算でも容易に実行できる代わりに時間計算量は大きいです。そこで互除法の現代的なバージョンでは、減算の繰り返しを剰余演算に置き換えています。これは $(3)$ より、次のことが言えるためです。

任意の整数 $N$ に対して

{\rm GCD}(m, n) = {\rm GCD}(n, m - Nn) \tag*{}

あるいは、$m\equiv r \mod n$ であるとき

{\rm GCD}(m, n) = {\rm GCD}(n, r) \tag{4}

コードはこんなに簡単になります。

func GCD_Remainder(m, n uint) uint {
	if m < n {
		m, n = n, m
	}

	for {
		if n == 0 {
			return m
		}

		m, n = n, m%n
	}
}

m$>$n$>$m%nなのでm、nは単調減少し、このアルゴリズムは必ず停止します。

${\rm GCD}(24140, 40902)$ を計算してみると、m、n の値は次のように変化していきます。ループ1回ごとに1回の剰余演算を実行します。

           40902            24140
           24140            16762
           16762             7378
            7378             2006
            2006             1360
            1360              646
             646               68
              68               34
              34                0

現代のプロセッサにはintくらいのサイズの整数に対して除算命令を標準で備えているものも多いですから、剰余演算は1ステップで実行できてしまいます。これ以上に速いアルゴリズムの存在が認識されたのは1960年代になってからでした。

二進アルゴリズム

除算は加減算よりも計算量が多く、プロセッサ組み込みの除算命令があっても実行に時間がかかります。エルサレム・ヘブライ大学のJ. Steinは1961年に剰余演算の代わりに減算とビットシフトの繰り返しを用いるアルゴリズムを考案しました4。

まず、次のことは古くから知られていました5。

$m$、$n$がともに偶数のとき

{\rm GCD}(m, n) = 2 \cdot {\rm GCD}(m / 2, n / 2) \tag*{}

したがって適当な非負整数 $k$ をとると

{\rm GCD}(m, n) = 2^k \cdot {\rm GCD}(m / 2^k, n / 2^k) \tag{5}

ちなみに $k$ が最大になるとき、$m / 2^k$、$n / 2^k$ のすくなくとも一方は奇数になります。

また、次のことも分かります。

$m$が偶数、$n$が奇数のとき

{\rm GCD}(m, n) = {\rm GCD}(n, m / 2) \tag{6}

なぜなら、$n$は奇数なので偶数 $m$ との公約数には素因数$2$は含まれないからです。

Steinのアルゴリズムでは、$(3)$ と $(6)$ から導かれる次の関係にも注目します。

$m$、$n$がともに奇数で$m > n$のとき

{\rm GCD}(m, n) = {\rm GCD}(n, (m - n) / 2) \tag{7}

これらに基づく二進GCDアルゴリズムのコードは次のようなものです。

func GCD_Binary(m, n uint) uint {
	if m == 0 {
		return n
	}
	if n == 0 {
		return m
	}

	var k uint = 0
	for m&1 == 0 && n&1 == 0 { // (5)
		k++
		m >>= 1
		n >>= 1
	}
	// ここで、mとnの少なくとも一方は奇数。
	if m&1 == 0 { // (6)
		m, n = n, m>>1
	}

	for {
		// ここで、少なくともmは奇数。
		for n&1 == 0 { // (6)
			n >>= 1
		}
		// ここで、mとnはともに奇数。
		switch { // (7)
		case m > n:
			m, n = n, (m-n)>>1
		case m < n:
			m, n = m, (n-m)>>1
		default:
			return m << k // (5)
		}
	}
}

mとnは単調減少し、このアルゴリズムは必ず停止します。

剰余演算をまったく使っていません6。代わりに減算とビットシフトを使います。${\rm GCD}(24140, 40902)$ を計算してみると、m、n および k の値は次のように変化していきます。ループの回数は剰余版の互除法の場合よりも若干増えますが、ひとつひとつの演算が安価になっています。

           24140            40902 12070/20451, [k = 1]
           20451             6035
           20451             6035
            6035             7208 3604, 1802, 901,
             901             2567
             901              833
             833               34 17,
              17              408 204, 102, 51,
              17               17

D. Knuthの "The Art of Computer Programming" には、二進アルゴリズムのかなりチューニングされた手順が掲載されています7。コードにするとこのようなものです。なお、このコードには負の数に対するシフト演算が現れるため、Go以外の言語に単純に書き換えると正しく動作しない場合があります8。

func GCD_TAOCP(u int, v int) int {
	if u == 0 {
		return v
	}
	if v == 0 {
		return u
	}

	var k uint = 0
	for u&1 == 0 && v&1 == 0 {
		k++
		u >>= 1
		v >>= 1
	}

	var t int
	if u&1 == 1 {
		t = -v
	} else {
		t = u >> 1
	}

	for {
		for t&1 == 0 {
			t >>= 1
		}

		if t > 0 {
			u = t
		} else {
			v = -t
		}

		t = u - v
		if t == 0 {
			return u << k
		}
	}
}

このアルゴリズムを多倍長演算に適用することもできそうです。多倍長演算にはGoだと math/big という標準パッケージが使えますね。

math/big 自体には Int 型に GCD() メソッドがあり、LehmerのGCDアルゴリズム9が実装されています。百ビット以上といった大きな整数では二進アルゴリズムの実装のほうがLehmerアルゴリズムを上回ったという結果も見つけました10が、いつか比較してみたいと思います。

浮動小数点演算を用いた二進アルゴリズム

二進アルゴリズムは除算命令をなくすことによって高速化を図っています。が、それがループの回数の増加を埋め合わせるほど効果を発揮しているかというと、微妙なところです。実際、あとで見るベンチマークでは、通常のint程度の大きさの数値について二進アルゴリズムは互除法にあと一歩及びません。

ループ回数増加の主な要因は、ビットシフトを1ビットずつ行っていることです。複数ビットのシフトをまとめて実行することができないでしょうか。

これについて、Steinはもうひとつの方式を提案しています4。それは、浮動小数点演算で用いられる正規化処理を利用して複数ビットのシフトを実行するというものです。先の方式では右シフトしましたが、こちらの方式では左シフトします。

方式の説明の前に、浮動小数点演算の仕組みについて概略を説明します。

まず記号を次のように定義します。

基数 $B$ での有限小数 $f$ が

  • 整数 $f_{expn}$
  • $1 \leq f_{frac} < 2_{(10)}$ となる基数 $B$ での有限小数 $f_{frac}$

によって

f = \pm f_{frac} \times B^{f_{expn}} \tag*{}

と表せるとき、$f_{expn}$ を $f$ の指数部、$f_{frac}$ を $f$ の仮数部と呼びます。

つまり浮動小数点数というものは、(2進法の場合) 整数部が常に1の小数を2の累乗倍した数です11。メモリ上では、次の図のように符号、指数部、仮数部が配置されます。

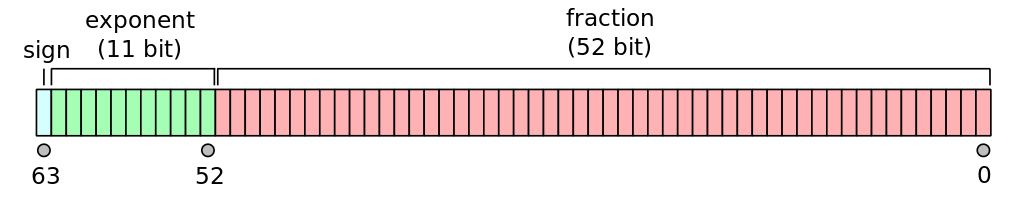
image.png
浮動小数点数のメモリ上の配置。IEEE 754 64ビット倍精度形式の例 (出所 File:IEEE 754 Double Floating Point Format.svg, Wikimedia Commons)

浮動小数点演算の結果は仮数部の整数部が1になるようにしなければなりません。例として 20.0 - 17.0 を基数を2として計算してみます。

$20.0_{(10)} = 1.01_{(2)} \times 2^4$、$17.0_{(10)} = 1.0001_{(2)} \times 2^4$ ですから、

\begin{array}{rr}
& 1.0100_{(2)} \times 2^4 \\
-\big{)} & 1.0001_{(2)} \times 2^4 \\
\hline
& 0.0011_{(2)} \times 2^4
\end{array}

しかし、このままでは仮数部の整数部に1が立っていません。そこで仮数部を左シフトさせると同時にシフトしたビット数だけ指数部の値を減らすことで調整すると、

\begin{array}{rr}
\phantom{ -\big{)} } & 1.1000_{(2)} \times 2^1
\end{array}

となり、3.0 の正しい形式での表現が得られます。この調整処理を正規化といいます。浮動小数点演算命令を実行すると、計算結果を格納する際に正規化が行われ、その際にビットシフトが行われます。

さて一方、$(4)$ により任意の整数 $N$ について

{\rm GCD}(u, v) = {\rm GCD}(v, \left| u - N v \right|) \hspace{2em} (u > v) \tag*{}

ですが、特に $N = 2^{u_{expn} - v_{expn}}$ のとき、

N v = 2^{u_{expn} - v_{expn}} \cdot v_{frac} \times 2^{v_{expn}} = v_{frac} \times 2^{u_{expn}} \tag*{}

ですから、

{\rm GCD}(u, v) = {\rm GCD}(v, \left| u - v_{frac} \times 2^{u_{expn}} \right|) \tag{8}

となります。右辺第2引数は減算の際の正規化によって仮数部のシフトが実行されます。つまり、先の二進アルゴリズムでは別々に行っていた減算と複数ビットのシフトが1ステップで実行されます。

このアイディアに基づくコードは次の通りです12。

import "math"

const signMask = 1 << 63
const fracBits = 52
const fracMask = 1<<fracBits - 1

func splitFloat64(f float64) (uint64, uint64, uint64) {
	bits := math.Float64bits(f)
	return bits & signMask, bits &^ (signMask | fracMask), bits & fracMask
}

func GCD_BinaryFloat(u, v float64) float64 {
	if v == 0 {
		return u
	}

	_, vExpn, vFrac := splitFloat64(v)
	for {
		if u == 0 || u == v {
			return v
		}

		_, uExpn, uFrac := splitFloat64(u)
		if u < v {
			u, v = v, u
			uExpn, vExpn = vExpn, uExpn
			uFrac, vFrac = vFrac, uFrac
		}

		u = math.Abs(u - math.Float64frombits(uExpn|vFrac)) // (8)
	}
}

$u > \left| u - v_{frac} \times 2^{u_{expn}} \right|$ である一方 $v$ との大小関係は自明ではないので、$u$ と $v$ を比較して適宜入れ替えています (後述)。このためu、vは単調減少し、このアルゴリズムはかならず停止します13。

splitFloat64() はfloat64型の数値を符号、指数部、仮数部のビット列に分解します。これで得た$u_{expn}$ と $v_{frac}$ をビット論理和で貼り合わせるだけで $v_{frac} \times 2^{u_{expn}}$ が作れます。また減算の際の正規化に伴って自動的にシフトが実行されます。先の二進アルゴリズムとくらべて、こちらの浮動小数点演算を用いた二進アルゴリズムは非常に単純なコードになりました。

${\rm GCD}(24140, 40902)$ を計算してみると、u、v の値は次のように変化していきます。ループの回数が互除法の場合よりやや増えはするものの、ループ1回ごとに若干のビット演算と1回の減算しか行っていません。

           24140            40902
            7378            24140
            5372             7378
            2006             5372
            2652             2006
            1360             2006
             646             1360
              68              646
             102               68
              34               68
               0               34

このアルゴリズムを多倍長演算に適用することもできます。その場合、上のコードで u と v を入れ替えるかどうかは $u_{expn}$ と $v_{expn}$ だけを比較して判断しても大丈夫です (Steinが示した手順ではそうなっています)。一方、$u$ と $v$ を比較して判断したほうがわずかですがループの回数を減らせます。int 程度のデータサイズでは整数の比較と浮動小数点数の比較とは実質的に違いがないですから後者が有利でした。仮数部のビット数が増えていけば前者が有利になっていくでしょう。

ベンチマーク

そのへんの適当なマシンで各アルゴリズムのベンチマークをとってみました。使用したのはGo 1.20.xで、最適化は有効なままです。

まずIntelチップ。Core i5のすこし昔のもの。

goarch: amd64
...
BenchmarkEuclidean-4     	   10000	       548.9 ns/op
BenchmarkRemainder-4     	   10000	       333.9 ns/op
BenchmarkBinary-4        	   10000	       359.5 ns/op
BenchmarkTAOCP-4         	   10000	       385.2 ns/op
BenchmarkBinaryFloat-4   	   10000	       294.3 ns/op

オリジナルのエウクレイデスの互除法がほぼダブルスコアで遅いのは当然ですが、剰余版の互除法はかなり強いですね。偶奇判定とシフトによる二進アルゴリズムはあと一歩及びませんでした (Knuthのカリカリにチューンしたように見えるコードがかえって遅いのも興味深いです)。勝者は 浮動小数点演算を用いた二進アルゴリズム でした。

M1チップ。

goarch: arm64
...
BenchmarkEuclidean   	   10000	       386.2 ns/op
BenchmarkRemainder   	   10000	       118.3 ns/op
BenchmarkBinary      	   10000	       292.4 ns/op
BenchmarkTAOCP       	   10000	       241.4 ns/op
BenchmarkBinaryFloat 	   10000	       306.1 ns/op

剰余版の互除法が圧倒的に強いです。ARM64の剰余演算専用命令 UREM の効果だと思われます。対して、二進アルゴリズムの3つについては順位がIntelと逆転しています。浮動小数点演算命令がそんなに速くないということでしょうか。浮動小数点演算より整数演算が得意という、Intelとは逆の特性を持っているようです。

goarchによる違いについては、いつかもう少し詳しく比較してみたいと思います。

結論。最大公約数を求めるための二進アルゴリズムは互除法より高速な (こともある) のです。

二進アルゴリズムみたび

二進アルゴリズムの課題として、シフトの繰り返しをまとめたいということがありました。要は下位ビットに0が並ぶ数を知りたいのです。

この数のことを NTZ (number of trailing zeros) と言ったりするそうです。愚直にループを回して数えるのではなくビットパターンの照合によって高速に数える手法があり、Goでも標準モジュールで提供されていました。これを使ってみます。

import "math/bits"

func GCD_BinaryNTZ(m, n uint) uint {
	if m == 0 {
		return n
	}
	if n == 0 {
		return m
	}

	var k int
	mS, nS := bits.TrailingZeros(m), bits.TrailingZeros(n)
	if mS < nS { // (5)
		k = mS
	} else {
		k = nS
	}
	m >>= k
	n >>= k
	// ここで、mとnの少なくとも一方は奇数。
	if m&1 == 0 { // (6)
		m, n = n, m>>1
	}

	for {
		// ここで、少なくともmは奇数。
		n >>= bits.TrailingZeros(n) // (6)
		// ここで、mとnはともに奇数。
		switch { // (7)
		case m > n:
			m, n = n, (m-n)>>1
		case m < n:
			m, n = m, (n-m)>>1
		default:
			return m << k // (5)
		}
	}
}

同様に、"The Art of Computer Programming" のバージョンも改善できます (負数のシフト演算についての注意は同じです)。

import "math/bits"

func GCD_TAOCPNTZ(u int, v int) int {
	if u == 0 {
		return v
	}
	if v == 0 {
		return u
	}

	var k int
	uS, vS := bits.TrailingZeros(uint(u)), bits.TrailingZeros(uint(v))
	if uS < vS {
		k = uS
	} else {
		k = vS
	}
	u >>= k
	v >>= k

	var t int
	if u&1 == 1 {
		t = -v
	} else {
		t = u >> 1
	}

	for {
		t >>= bits.TrailingZeros(uint(t))

		if t > 0 {
			u = t
		} else {
			v = -t
		}

		t = u - v
		if t == 0 {
			return u << k
		}
	}
}

なお、math/bigパッケージにも TrailingZeroBits() がありますからこのアルゴリズムは多倍長演算にも適用できそうです。

ベンチマークに再挑戦してみましょう。

Intelチップ。

goarch: amd64
...
BenchmarkEuclidean-4     	   10000	       518.8 ns/op
BenchmarkRemainder-4     	   10000	       334.2 ns/op
BenchmarkBinary-4        	   10000	       358.1 ns/op
BenchmarkTAOCP-4         	   10000	       410.2 ns/op
BenchmarkBinaryFloat-4   	   10000	       297.5 ns/op
BenchmarkBinaryNTZ-4     	   10000	       222.4 ns/op
BenchmarkTAOCPNTZ-4      	   10000	       218.9 ns/op

NTZ版の二進アルゴリズムの圧勝です。

M1チップ。

goarch: arm64
...
BenchmarkEuclidean-8     	   10000	       496.4 ns/op
BenchmarkRemainder-8     	   10000	       115.1 ns/op
BenchmarkBinary-8        	   10000	       284.9 ns/op
BenchmarkTAOCP-8         	   10000	       232.3 ns/op
BenchmarkBinaryFloat-8   	   10000	       309.6 ns/op
BenchmarkBinaryNTZ-8     	   10000	       154.0 ns/op
BenchmarkTAOCPNTZ-8      	   10000	       105.5 ns/op

剰余版の互除法は手強い。NTZ版の二進アルゴリズムはKnuthチューニングで辛勝しました。

結論。最大公約数を求めるための二進アルゴリズムは互除法より高速な (ようにできる) のです。

メタデータ

この記事のライセンス

クリエイティブ・コモンズ・ライセンス
この記事はCC BY-SA 4.0（クリエイティブ・コモンズ 表示 4.0 継承 国際 ライセンス）の元で公開します。

改訂履歴

2023-07-01

  • 「浮動小数点演算を用いた二進アルゴリズム」---負数の右シフトについての注意を追記。
  • 「ベンチマーク」---結果の桁ずれを訂正。

2023-07-03

  • 「二進アルゴリズム」---コードのインデント修正、コメント訂正。
  • 「浮動小数点演算を用いた二進アルゴリズム」---整数の比較と浮動小数点数の比較について補記。
  • 「二進アルゴリズムみたび」---新規作成。
  • 誤字修正。
  • 記事のライセンスをCC BY-SA 4.0 Intl.とする。

2023-07-05

  • 多倍長演算への適用について加筆。
  • ほか微加筆。
  • 不要な空白を除去。

  1. 『原論』では$1$は「単位」と呼ばれ、$2$以上の自然数が「数」とされます。 ↩

  2. 田村松平(編) (1972).『世界の名著9: ギリシアの科学』「エウクレイデス 原論」第七巻、中央公論社. pp. 331f. ↩

  3. エウクレイデスの時代にはまだ$0$はなかったはずですが、この後で掲載するコードとの一貫性のためにパラメータが$0$を含む場合も考慮しました。また関数の引数は非負整数に正規化されているものとします。以下同じ。 ↩

  4. Stein, J. (1967). "Computational problems associated with Racah algebra", Journal of Computational Physics, 1 (3): 397–405. DOI:10.1016/0021-9991(67)90047-2. ↩ ↩2

  5. 中国で紀元前後に成立したと見られる『九章算術』や、それよりさらに2、3世紀遡ると見られる『算数書』には、分数を約分する際は「(分母と分子を) 半分にできる限り半分にする」という意味の記述が見えます。 ↩

  6. 整数の偶奇の判定にも i % 2 ではなく i & 1 の値を用いています。ほとんど影響はないと思いますが……。 ↩

  7. Knuth, D. (1997). "The Art of Computer Programming", Volume 2: "Seminumerical Algorithms" (3rd Edition). pp. 338ff. ISBN 978-0-201-89684-8. 日本語版 (アスキー刊) pp. 317ff. ISBN 978-4-7561-4543-7. ↩

  8. KnuthはTAOCPの中では一貫して、負数に対する右シフト演算を算術シフトとして議論しています。Goなど比較的多くの言語が実際にそうです。しかし例えばC/C++では、負数に対する右シフト演算の結果は処理系定義であると規定されているため、論理シフトなどが実行されることもありえます。 ↩

  9. "Lehmer's GCD algorithm", Wikipedia. ↩

  10. Jebelean, T. (1993). "A generalization of the binary GCD algorithm". International Symposium on Symbolic and Algebraic Computation. DOI:10.1145/164081.164102. ↩

  11. $0.5_{(10)} \leq f_{frac} < 1$ とする流儀もありますが、ここでは現在よく使われているIEEE 754倍精度形式の流儀にならいます。ちなみに、0 などのように整数部に 1 が立つ数の倍数では表せないものは例外ルールを設けて扱うことになっています。 ↩

  12. Steinの時代には浮動小数点演算命令はまだありませんでしたが、浮動小数点演算を想定したNORMALIZEという命令を持つシステムが存在したとのことです (CDC 6000シリーズやIBM 1100など)。これは、レジスタに格納された数値を必要なだけシフトするとともにシフトしたビット数だけ別のレジスタの値を増減させるという処理を一命令で実行するものでした。SteinはNORMALIZE命令によって得られるシフトのビット数の情報も用いた手順を示しています。しかし、ここで示すコードの通り、このアルゴリズムでは正規化によるシフトのビット数を具体的に知る必要はありません。 ↩

  13. なお、処理の都合で関数の引数が浮動小数点型になっていますが、整数にならないような数値を与えると確実に暴走しますので注意してください。float64型で表せる整数は $2^{53}-1$ 以下です。 ↩

11
5
13

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
11
5