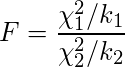この記事では、初学者用に統計学でつまづきやすい(自分が理解に時間がかかった)部分をメインに解説します。
目次は以下の通りです。
目次
1 統計的思考
2 分散の考え方
3 回帰の考え方
4 実験計画法 F値と分散分析
統計学を学習するメリット
1 機械学習・データサイエンスの基本的な考え方は統計学がベースとなっている
2 意思決定に関して、データ・事実から客観的に考えることができる
統計検定2級合格を目指して、最近統計学にかなりの時間を費やしている上で、個人的に感じたメリットになります。
統計学の罠
「統計学」という学問は最初とっっつきづらいです。特に理系でない人からすると、分散とか標準偏差ってナニソレ?って感じだと思います。さらに、勉強していくと分散・標準偏差なんて可愛く、数式や検定・推定の考え方がイチイチ厳格でややこしいです。慣れるまではしばらく時間がかかりました。
故に僕の場合、「理解できた→面白い」となるまである程度の勉強時間がかか印象でした。。
ただ、慣れてきて、何をやっているのか全体感が掴めてくると、急に勉強が楽しくなってきました。
できるだけすんなり統計学を理解ためのポイントをまとめて伝えられればと思います。
全ての知識を網羅している訳ではないので、足りない部分はわかりやすい書籍や他の方の記事を探して、適宜補ってもらえればと思います。
1統計的思考
Q統計や統計的思考が何の役に立つのか?
統計学を勉強していて全体像が掴めない状態だと頻繁に問いかけたくなります。
この問いに、答えを持っておかないと勉強するモチベーションや面白さが少なくなってしまう気がします。
答えは、使う人によって様々なので、自分なりに、答えをだしていきましょう。
勉強する人が、どう言った立場で、何に使いたいかにより、主に
・学者・研究者ならば、実験結果を偶然ではなく、効果があると証明するため
・経営者ならば、会社の方向性・事業を決めるための意思決定の指標
が挙げられます。
では、そう言った立場にない一般人が何のご利益があるのか?と言う部分にも、一応答えはあると思ってます。
今の僕の答えとしては、
1 人間の直感を補う意思決定のツールとして有用である。
2 本当の原因がどこになるかを見抜くリテラシー
が統計学を勉強するメリットではないかと思います。
ただ、仕事で統計の知識を必要としない人にとってはモチベーションは薄いと思いますし、学習コストも高いので無理に役立てようと思って勉強することではないとは思います。
人間はよく判断を間違えます。それが、脳の仕組みによるものだそうです。
人間の脳はバイアス(偏見)を持っていますが、それは動物(サル)から、知的生物になった人間の進化の過程や、脳科学的にも、構造上逃れられない副産物ことだそうです。
"直感"で考えたり、「なんとなくこうだろう〜」と人間がジャッジを下せるのは、曖昧な状況でも意思決定しなきゃいけないので、脳が曖昧な判断でもスピーディーにこなせるよう進化してきたそうです。故に、バイアスは副産物的に人間の脳に付き纏います。
統計学の大きな認知のバイアスは以下の2つです。
1 実際は「ない」のに「ある」と思ってしまう。(第一種の過誤)
2 実際は「ある」のに、「ない」と思ってしまう。(第二種の過誤)
より詳しく言うと、
1 偶然起きた、たまたまの事象を、何か意味のあることに繋げてしまうこと
2 偶然では無い効果があることなのに、偶然だと思ってしまう。
になります。
そんなバイアスの中で、ベストと言える意思決定をしていこうと言うのが、統計学の重要な役割になります。
統計的に意思決定するためには、事実としてのデータが必要な訳ですが、
データを可視化・定量化することがなぜ重要なのか?と言う疑問もあるかと思います。
それは、人間の脳がデータをただ数値の羅列として表示してある部分から、意味を見出すのは難しいからです。
つまり、人間の認知能力を最大限に生かせる形式が、データの可視化(グラフにするなど)なのです。
統計学は、確率論をベースにしているので絶対の正解などありません。(世の中、生きていて。多くくこともそうですが)
統計学は、真実を見抜く万能な水晶ではなく、限られたリソースの中で最善の解を見出すものであると言えます。
2 分散の考え方
分散とは?
データのバラツキの指標 「平均平方」とも呼ばれる。
分散の求め方①
𝑉𝑎𝑟[𝑋]=𝐸[(𝑋−μ)2]
上式のように、なぜ分散は偏差の二乗 =(観測値ー平均)**2 なのか?
それは、真ん中(平均)からのばらつき(偏差)を見るためです。
分散の求め方②
分散(variance)の意味
V𝑎𝑟[𝑋]=𝐸(𝑋2)–[𝐸(𝑋)]2
分散=二乗の期待値 − 期待値の二乗
とも表されます。
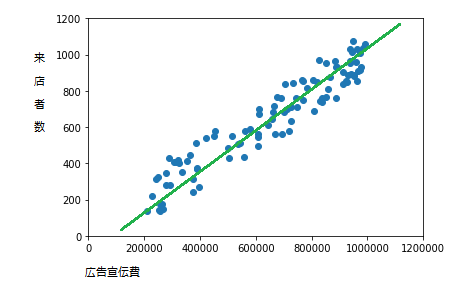
3 回帰の考え方
分散で学んだように、正規分布に従う事象の場合、実際平均ピッタリの数が現れることは稀なことで、平均を中心に散らばっています。
実際の計測された値は誤差を含んでいる。このことから、
真の予測と言うものがあり、その予測からバラツキを伴って現れる。という発想をもとに、現象を分析しようするのが回帰の考え方です。
4 実験計画法
実験計画法
1反復実施・・誤差によるバラツキを評価するため(バラツキがたくさんが比較できる)
2無作為化(ランダム化)・・背景要因による影響を偶然誤差に変える。
3局所管理・・実験環境の均一化
完全無作為化法・・反復実施と無作為かを満たす実験法
Qなぜ反復実施するのか?
正規分布モデルに当てはめ、偶然的なバラツキ(分散)を評価する。
Qなぜ無作為化するのか?
もし、無作為化しないと実験要因以外の背景要因との交絡の効果を取り除けないから!
データがばらつくのは、コントロールされた水準によるバラツキ(水準)と、コントロールされていない(偶然誤差)による2つがある。
5 F値
F値とは?
(厳密な定義)
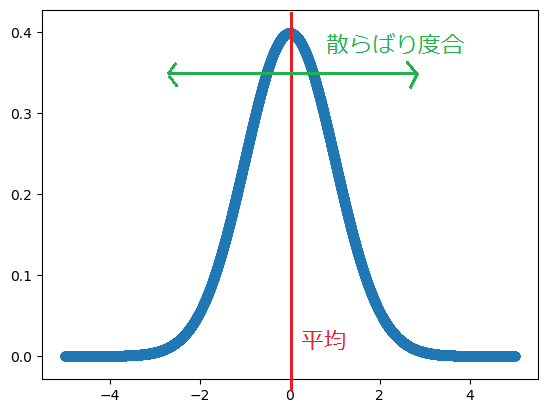
F分布は、自由度がk1,k2のカイ二乗分布χ1,χ2が互いに独立である場合に、
次の式から算出されるFが従う確率分布のことです
つまり、分散の比がF値
上辺 分散1(カイ二乗値) (処理平均平方) 群間変動
下辺 分散2(カイ二乗値) (誤差平均平方) 群内変動
”捉え方” 分散の比がカイ二乗分布に従う
F検定とは?
分散が等しいかどうかを調べる検定 (等分散性の検定)
→T検定をする前に、分散が等しいかどうか調べる必要がある。(分散が等しくなければ、有名なステューデントT検定はできない)