目次
1. 線形代数
行列
行列の用途
- ベクトルの変換
- 1,1 が 5, 5 になるような単純な変換ではない、バリエーションのある変換
- 連立方程式
- 機械学習のパラメータ
- その他さまざまな分野
連立方程式
$ x_1 + 2x_2 = 3 $
これだと方程式は解けない
$ 2x_1 + 5x_2 = 5 $
これで解が求まる
連立方程式を行列で表す
この連立方程式を
\begin{equation}
\left\{ \,
\begin{aligned}
x_1 + 2x_2 = 3 \\
2x_1 + 5x_2 = 5
\end{aligned}
\right.
\end{equation}
$ A \vec{x} = \vec{y} $ こんなふうに行列とベクトルで表すことができる。
\begin{pmatrix}
1 & 2 \\
2 & 5
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix}
=
\begin{pmatrix}
3 \\
5
\end{pmatrix}
行列とベクトルの積&行列と行列の積
左側は行単位、右側は列単位の「要素」同士での積の和が、演算結果の行列の要素になる。
\begin{pmatrix}■&□\\□&□\end{pmatrix}
\begin{pmatrix}■&□\\□&□\end{pmatrix}\\
■\times■
\begin{pmatrix}□&●\\□&□\end{pmatrix}
\begin{pmatrix}□&□\\●&□\end{pmatrix}\\
●\times●
\rightarrow
\begin{pmatrix}(■\times■)+(●\times●)=a& b \\c&d\end{pmatrix}
さらにこれを、
左の1行目と右の2列目、
左の2行目と右の1列目、
左の2行目と右の2列目、
という組み合わせで同様の計算をすることで
\begin{pmatrix}a & b \\ c & d\end{pmatrix}
が求まる。
行列(ベクトル)の積のサイズチェック
2x2 と 2x1 のベクトルの積をもとめると、
左の行数である2 x 、右の列数の1 で、 2 x 1 のベクトルが結果のサイズになる。
たとえば
4x3 と 3x2 なら、(4 x 3)(3 x 2) 4x2 と瞬時にわかる
※ 左の列数と右の行数の数字が一致しない場合は、積の計算自体なりたたない。
連立方程式を解く
行基本変形を使って解く
- 行を入れ替える
- 行を何倍かする
- ある行に別の行を何倍かして加える
固有値、固有ベクトル
正方行列について $ A\vec{x} = λ\vec{x} $ こんな関係が成り立つような
$ λ と \vec{x} $ をそれぞれ 固有値、固有ベクトル という。
ベクトルにある行列を掛けているのに、
もとのベクトル(のラムダ倍)のベクトルになってしまう、ということ。
まるで行列Aをこの$ \vec{x} $ に掛けているときは、λと同様に見做せるという見方もできる。
- 具体例
\begin{pmatrix}1 & 4 \\ 2 & 3\end{pmatrix}
\begin{pmatrix}1 \\ 1\end{pmatrix}
=
\begin{pmatrix}5 \\ 5\end{pmatrix}
=
5
\begin{pmatrix}1 \\ 1\end{pmatrix}
右辺の5がλ(固有値)
つまり行列×ベクトルした場合と、
スカラー×ベクトルした結果が同じになっている。
※ 固有値は2x2の場合は2つ求まる
※ 固有ベクトルも固有値に対してそれぞれ一つもとまるので、2つ求まる。
固有ベクトルというのは、具体的な値が求まるわけではなく、特定の比率が求まるだけ。
求め方
$ A\vec{x} = λ\vec{x} $ 求めるにはどうすればよいか
移項して $ \vec{x} $ で括る
$ A\vec{x} - λ\vec{x} = 0 $
ここでλはスカラーなのでAから直接引き算ができないので、λIとして、
$ (A - λI)\vec{x} = \vec{0} $ とする。
$ \vec{x} = \vec{0} $ だと自明な解になってしまい、無意味なので、
$ \vec{x} ≠ \vec{0} $ とする。
もし $ (A - λI) $ が逆行列をもってしまったら、 $ \vec{x} ≠ \vec{0} $ の前提が成り立たなくなる。両辺にAの逆行列を掛けてみるとわかる。
→ $ (A - λI)^{-1}(A - λI)\vec{x} = (A - λI)^{-1}\vec{0} $ という形になってしまう。
$ (A - λI)^{-1}(A - λI) $ この部分はもとの行列と逆行列を掛けているので $I$ になる。
そのため、$ \vec{0} $ に何を掛けても $ \vec{0} $ なので、$ \vec{x} = \vec{0} $ になってしまう。
ということは、$ (A - λI) $ が逆行列を持たなければうまくいく。
これが成り立てばよい。
$ det(A - λI) = 0 $
※ det()は行列式
\begin{vmatrix}
1-λ & 4 \\
2 & 3-λ
\end{vmatrix}
= 0
これをλについて解く。
行列式を求める公式より
$ (1-λ)(3-λ) - (4 \times 2) = 0$
あとは普通に2次方程式を解くだけ。
$ λ^2-4λ-5 = 0 $
$ (λ-5)(λ+1) = 0 $
$ λ = 5, -1 $ これで固有値が求まった。
次に固有ベクトル
$ A\vec{x} = λ\vec{x} $ λに、2つ求まった固有値をそれぞれ代入して、$ \vec{x} $を求める
(i) λ=5 の場合
\begin{pmatrix}1&4\\2&3\end{pmatrix}
\begin{pmatrix}x_1\\x_2\end{pmatrix}
=5
\begin{pmatrix}x_1\\x_2\end{pmatrix}
\rightarrow x_1 = x_2 \\
\rightarrow \vec{x} = \begin{pmatrix}1\\1\end{pmatrix}の定数倍
(ii) λ=-1 の場合
\begin{pmatrix}1&4\\2&3\end{pmatrix}
\begin{pmatrix}x_1\\x_2\end{pmatrix}
=-1
\begin{pmatrix}x_1\\x_2\end{pmatrix}
\rightarrow x_1 = -2x_2 \\
\rightarrow \vec{x} = \begin{pmatrix}2\\-1\end{pmatrix}の定数倍
固有値分解
固有値と固有ベクトルを用いて、行列を分解する。
$ A\vec{x} = λ\vec{x} $ となる複数の λ $ \vec{x} $ をまとめて表現する。
分解のメリット
- 行列の似たような特徴を見つけることができるようになる。(分類などに使える)
- 値の小さな固有値は全体に与える影響が小さいので、これらを無視して(次元削減)計算コストを下げる。
- $ A^n $ の計算を楽にする。
めざす形は、
$ A = VΛV^{-1} $
Aはもとの行列。これを右辺のように、
V = 固有ベクトルを横に並べた行列、
Λ = 固有値を主対角線上に並べた行列
とVの逆行列
これらの積という形で表す。
具体例
\begin{pmatrix}1&4\\2&3\end{pmatrix}
=
\begin{pmatrix}1&1\\1&-\frac{1}{2}\end{pmatrix}
\begin{pmatrix}5&0\\0&-1\end{pmatrix}
\begin{pmatrix}\frac{1}{3}&\frac{2}{3}\\\frac{2}{3}&-\frac{2}{3}\end{pmatrix}
\\A = VΛV^{-1}
特異値分解
正方行列でない長方形でも、固有値分解のようなものをしたいときにどうすればよいか??
$ M\vec{v} = σ\vec{u} $
$ M^T\vec{u} = σ\vec{v} $
このような、\vec{v}から\vec{u}を経由して、Mの転置を掛けるともとの\vec{v}に戻ってくるような特殊なものを用いることで、正方行列の固有値分解 $ \acute{の}\acute{よ}\acute{う}\acute{な}\acute{も}\acute{の} $ を行う。
$ M = USV^T $
※ S の代わりに ∑ で表すことも多い。
求め方
$ MV = US $ さっきの式を行列で表したもの
$ M = USV^T $ この$ V^T $ は逆行列ではなくて、転置でよい。直交行列の性質による。
$ M^TU = VS^T $ これもさっきの式を行列で表したもの
$ M^T = VS^TU^T $ 同様に$ U^T $ は逆行列ではなくて、転置でよい。直交行列の性質による。
$ MM^T $ はこう表せる
$ MM^T = USV^TVS^TU^T $
$ V^TV $ は単位行列になるので、
$ MM^T = USS^TU^T $
これはまるで、$ MM^T $ を固有値分解しているような形になる。
もとの行列を転置した行列と掛けてしまっているので、それっぽくSS^Tに出てくるλのルートを取ることで、もとのMの固有値のようなもの(これを特異値と呼ぶ)を算出している。
求め方の具体例
M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}
の特異値分解をする。
MM^T =
\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}
\begin{pmatrix}1&3\\2&2\\3&1\end{pmatrix}
=
\begin{pmatrix}14&10\\10&14\end{pmatrix}
この行列を固有値分解する。
$ λ = 4, 24 $となる
λ=4のとき
t\begin{pmatrix}-1\\1\end{pmatrix}\\
λ=24のとき
t\begin{pmatrix}1\\1\end{pmatrix}\\
tは任意の実数(t≠0)
このとき固有ベクトルを、「長さ1」になるように調整する。
λ=4のとき
\begin{pmatrix}-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{pmatrix}\\
λ=24のとき
\begin{pmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\end{pmatrix}
MM^T = \begin{pmatrix}14&10\\10&14\end{pmatrix}=
\begin{pmatrix}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}} \end{pmatrix}
\begin{pmatrix}24&0\\0&4\end{pmatrix}
\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}} \end{pmatrix}
これと同様のことを、$ M^TM について行う。 (固有値分解する)
M^TM =
\begin{pmatrix}1&3\\2&2\\3&1\end{pmatrix}
\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}
=
\begin{pmatrix}10&8&6\\8&8&8\\6&8&10\end{pmatrix}
λ= 4, 24 で同じ
固有ベクトルは
v_1=
\begin{pmatrix}
\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{3}}
\end{pmatrix}
,
v_2=
\begin{pmatrix}
\frac{1}{\sqrt{2}}\\
0\\
-\frac{1}{\sqrt{2}}
\end{pmatrix}
,
v_3=
\begin{pmatrix}
\frac{1}{\sqrt{6}}\\
-\frac{2}{\sqrt{6}}\\
\frac{1}{\sqrt{6}}
\end{pmatrix}
特異値分解の結果
M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}
=
\begin{pmatrix}
\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}
\end{pmatrix}
\begin{pmatrix}2\sqrt{6}&0&0\\0&2&0\end{pmatrix}
\begin{pmatrix}
\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{3}}&\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{6}}&-\frac{2}{\sqrt{6}}&\frac{1}{\sqrt{6}}
\end{pmatrix}
サイズチェック
$ 2 \times 3 = (2 \times 2)(2 \times 3)(3 \times 3) $
線形代数まとめ
基本的な四則演算的な演算や逆行列の求め方は以前学習済みであったため復習となった。
固有値分解と特異値分解については、今回初めて計算方法と意味を知った。
固有値分解は正方行列のみの道具であるが、
特異値分解は、正方行列における固有値分解と似たようなことを正方でない行列でも行いたいというモチベーションに由来している。それを実現するためのアイデアとして $ MM^T $ と $ M^TM $ の固有値分解を考えてそれぞれの固有値のルートを取るというのは直感的にも受け入れやすいと感じた。
2. 確率統計
確率統計
統計とは
木を見てばかりでなく森を見る、ということを数理的に行う。事象を要約する。
記述統計$ \rightarrow $ 母集団がそろっている前提
推測統計$ \rightarrow $ 全体を調査できないときに標本を取り出して分析
確率変数と確率分布
例えば、コインを4回投げたときの表の出る数を確立変数と考える。
数値になればどのような設定の仕方もありうる。
サイコロの目の3倍、とか、偶数のときは10倍、奇数のときは4とか、いくらでも設定できる。
期待値
事象 x1 x2 ... xn
確率変数 f(x1) f(x2) ... f(xn)
確率 P(x1) P(x2) ... P(xn)
\sum_{k=1}^n f(x_k)P(x_k) 離散の場合
\int f(x_k)P(x_k)dx 連続の場合
分散共分散
分散:データの散らばり具合
個々のデータと平均値(期待値)とのズレ具合。
分散 Var(f) \\
= E\Bigl( f(X=x) - E(f)^2 \Bigr) \\
= E \Bigl( f^2(X=x) \Bigr) - \Bigl( E(f) \Bigr)^2
共分散:2つのデータ系列の傾向の違い。
正の値なら似た傾向がある。
負の値なら逆の傾向がある。
共分散 Cov(f, g) \\
= E \Bigl( (f(X=x) - E(f)) (g(X=x) - E(g))) \Bigr) \\
= E(f^2(X=x)) - (E(f))^2
標準偏差
分散のルートを取ることにより、単位をあわせる。
$ 標準偏差 = \sqrt{分散} $
確率分布
ベルヌーイ分布
- 結果が2のみのもの
- 例えばコインの裏表とか
- P=1/2 でなくても扱える。
マルチヌーイ分布
- 結果が2のみでなくて複数あるもの。
- 例えばサイコロ
- 同様に確かでなくても扱える。
二項分布
- ベルヌーイ分布を何度も施行したときの分布
- 真ん中が山になる。
$ P(x|\lambda, n) = {}_n C _x \lambda^x(1-\lambda)^{1-x} $
ガウス分布(=正規分布)(=ノーマルディストリビューション)
2つの指数関数を左右に並べたような形になっている。
expの中の$(x-μ)^2$ のところで山になるような工夫がされている。
検定
推定量と推定値
推定量(estimator)
パラメータを推定するために利用する関数のイメージ。推定関数とも呼ぶ。
推定値(estimate)
実際に試行を行った結果から計算した値
これらは区別することもしないこともある。
$ 真の値をθとすると、推定のときは、 \hat{θ} と表す $
標本平均
一致性
サンプル数が増えれば母集団の値に近づくという性質
不偏性
サンプル数に関わらずその期待値は母集団の値と同様。
「偏っていない」という意味。 つまり、 $ E(\hat{θ}) = θ $
標本分散
\hat{σ}^2 = \frac{1}{n}\sum_{i=1}^{n}(x_1 - \bar{x})^2
一致性は満たすが、不偏性は満たさない
思考実験
たくさんデータがある場合と、少ないデータの場合とどちらがよりばらつくか?
☆少ないデータのほうがばらつきは少ないはず。
つまりこのままだと、バラツキを過小評価してしまっている。
それで1を引いて分母を小さくすることで適正にしている、という直感的な理解。
\hat{s}^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_1 - \bar{x})^2
これを 不偏分散 という。
確率統計まとめ
確率統計では表に示された具体的な値をもとにする問題が多い記述統計ではデータが目に見えているので、比較的何が起きているのか、事象が見えやすいが、推測統計で、とくにE(x) V(x) などと式でまとめて表す場合は、データが見えないためより深い理解が必要である。
具体的なデータをイメージしながら考えるのと同時に、これらは公式を使った式変形が重要になるため、覚えるところは覚えるしかない。
また、各種の分布関数や期待値、標準偏差などの求め方も覚えるところは覚えて、可能であれば導出できるようにしておくほうがよいと思った。
確率統計・公式補足
2変数
$ E(X+Y) = E(X) + E(Y) 独立でなくても成立 $
$ V(X+Y) = V(X) + V(Y) 独立の場合のみ成立 $
3変数
$ E(X+Y+Z) = E(X) + E(Y) + E(Z) 独立でなくても成立 $
$ E(XYZ) = E(X)E(Y)E(Z) 独立の場合のみ成立 $
$ V(X+Y+Z) = V(X) + V(Y) + V(Z) 独立の場合のみ成立 $
線形性(統計2級や高校数学にも載っている公式)
$ E(sX + t) = sE(X) + t $
$ V(sX + t) = s^2E(X) $
3. 情報理論
情報理論
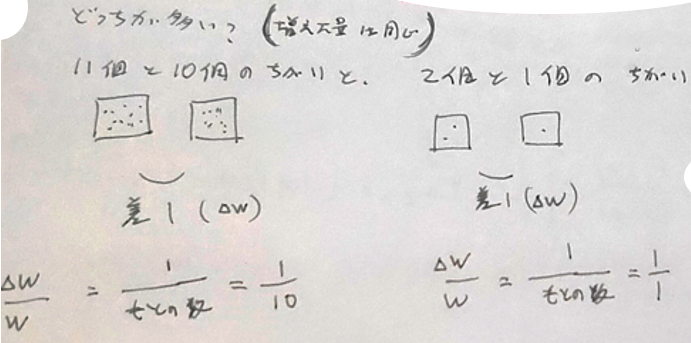
11 - 10 = 1
2 - 1 = 1
どちらも差は1で、なぜ見分けやすさに差が出るのか???
→ もとになる数との比率をみればよい。
何か荷物を持っているときに、
100g 持っているところ 10g の荷物を追加したら気づく場合でも
1kg 持っているところに 10g を追加しても人間の感覚的には気づかないと言われている。
自己情報量
$$
\frac{1}{w} の積分
$$
$$
\int \frac{1}{w}dw = log|w| + C
$$
$$
I(x) = -log(P(x)) = log(w(x))
$$
情報の珍しさ
情報が増えるとエネルギーが必要になるイメージ
対数の底が2のとき、単位は bit
対数の底がeのとき、単位は nat
4個の情報を送るためには、ボタンは2つあればよい。
8個の情報を送るためには、ボタンは3つあればよい。
つまり $ log _2 $ を取った数だけあればよい。
シャノン・エントロピー
シャノン・エントロピーとは、自己情報量の期待値のこと
H(x) = E(I(x))
= -E( logP(x) )
= -∑{ P(x) logP(x) }
確率が低くなればなるほどレア度があがるので、情報量も高くなる。
カルバック・ライブラー・ダイバージェンス
同じ事象、確率変数における異なる確率分布 P、Q の違いを表す
距離のようなもの、とよく言われるらしい。
距離とは言えないけど、距離のようなもの。擬距離、などとも。
※ P, Q を入れ替えると結果が変わるので、厳密な意味での距離とは言えないらしい。
D_{kl}(P||Q)
= E_{x\sim p}
\begin{bmatrix}log\frac{P(x)}{Q(x)}\end{bmatrix}
= E_{x\sim p}
[logP(x) - logQ(x)]
もともとQを考えていたのに、
実はPだった、という場合を考えると、__新たにわかったP__で平均をとる、と解釈できる
「新たにわかったP」は「情報利得」と説明されることもある
D_{kl}(P||Q)
Q:古い状態のQを、
P:新しく得たPという分布から眺めたときは、どのくらい違っているか、ということを表すのが、
カルバック・ライブラー・ダイバージェンス
D_{kl}(P||Q)
= \sum_x P(x) log \frac{P(x)}{Q(x)}
交差エントロピー
- KLD の一部分である。
- でも、KLDとは関係なしにQについての自己情報量をPの分布で平均したものとして作られたらしい。
予定していた暗号表に載っていない事象が起きたので、余計な暗号Pを送る、という例の紹介。
I(Q) について、Pで平均をとる。
情報理論まとめ
今までとくに詳しく学習したことがなかった分野だが確率分野と対数計算を以前から身につけていたため理解はできた。
しかし、交差エントロピーはある程度の理解にとどまっているため、今後MLの講義の中で出てきたときに不明点が明らかになったら復習が必要。