はじめに
このページでは最近話題になっている機械学習の手法CatBoostの簡単な概要及び実装例をご紹介します。
CatBoostの概要
CatBoostは勾配ブースティングの一種で、ロシアの検索エンジンで有名なYandex社によって開発され、2017年4月にリリースされました。実際Yandexの検索アルゴリズムにはCatBoostが使用されてるそうです。
名前の通り**Categorical Features (カテゴリカル変数)**が多いデータに強いです。
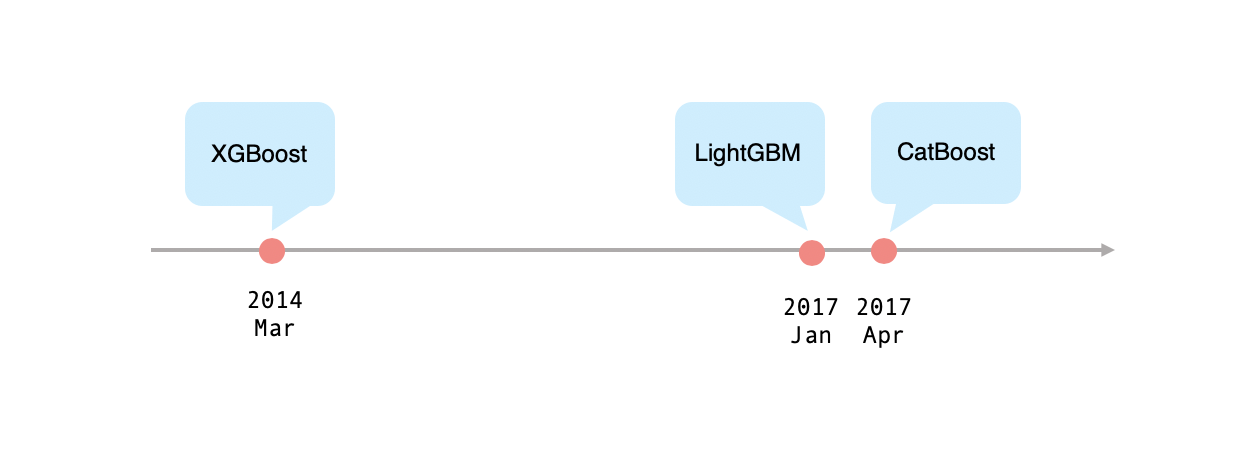
ここ数年注目を浴びてきた勾配ブーストモデルには XGBoost (2014年3月) や LightGBM (2017年1月) もありますが、CatBoostは最も新しく、場合によっては、この2つを上回る精度を出すことも可能です。
CatBoost のアルゴリズム
こちらの論文を参考にさせて頂きながら、CatBoostのアルゴリズムを簡単に説明していきたいと思います。
カテゴリカル変数の処理
機械学習で扱う生データには、性別、学歴、所在地など、そのままでは学習に使えないカテゴリカル変数がよくあります。なので、それらの変数をモデルに投入する前に何らかの方法で処理してあげる必要があります。CatBoostには、このカテゴリカル変数をより高度に処理してくれるアルゴリズムが含まれています。ここではメインとなる3つの点を紹介します。
1. Greedy TS
カテゴリカル変数の処理でよく使われるテクニックに、カテゴリーごとに [1,0] でラベルする one-hot-encodingがあります。one-hot-encoding の問題点は、カテゴリの種類が多い変数では、膨大な数の特徴量が作られてしまい、モデルの精度を下げる可能性がある点です。その問題を解決する為に、**各カテゴリーごとのyの期待値(Target Statistics: TS )**をもとに、カテゴリーを分類する方法が考え出されました。つまり、元々のカテゴリカルデータを、カテゴリーごとのTSに置き換えグループ化することで、元の情報をできる限り保持しながら、モデルに投入できる変数に置き換えるのです。グループ化の閾値は、logloss, Gini index, MSEなどによって決めることができます。
ただ、各カテゴリーごとのTSを求めるのに、yの条件付き確率をダイレクトに利用してしまうと、ノイズやサンプル数の偏りに強く影響してしまいます。
その為CatBoostでは Greedy にTSを求めることでノイズの影響を滑らかにします。
この時注意しなくてはならないのが、TSを求めるのに y を使っている為、target leakageとなり、学習データに過学習してしまう危険性があるということです。
そこで、全ての学習データを使ってTSを求めず、サブデータセット$D_k$を使いTSを求めることで、target leakageを防ぐことができます。
\mathcal{D}_{k} \subset \mathcal{D} \backslash\left\{\mathbf{x}_{k}\right\}
各サンプルのTSの値 $\hat{x}_{k}^{i}$は、下のように求められます。この時、a は a>0となるパラメター、pは一般的には目的値の平均値を使います。
\hat{x}_{k}^{i}=\frac{\sum_{\mathbf{x}_{j} \in \mathcal{D}_{k}} \mathbb{1}_{\left\{x_{j}^{i}=x_{k}^{i}\right\}} \cdot y_{j}+a p}{\sum_{\mathbf{x}_{j} \in \mathcal{D}_{k}} \mathbb{1}_{\left\{x_{j}^{i}=x_{k}^{i}\right\}}+a}
また、CatBoostではデータのサブサンプリングにOrdered TSという特別な方法を使います。
Ordered TSとは簡単にいうと、各サンプルに時点を与え、過去のデータのみを利用してyを推定するいわゆる online machine learningと同様のテクニックです。実際は元々のデータは時系列ではないので、時点はランダムに割り振られれます。
2. Ordered Boosting
勾配法では、損失が小さくなるように、各ステップで勾配 $h^t$ を計算することで、最適化をおこないます。
h^{t}=\underset{h \in H}{\arg \min } \frac{1}{n} \sum_{k=1}^{n}\left(-g^{t}\left(\mathbf{x}_{k}, y_{k}\right)-h\left(\mathbf{x}_{k}\right)\right)^{2}
しかし、一般的な勾配法にはある潜在的な問題が存在します。先ほどTSを計算する際にあげた問題と同様に、勾配法では目的変数 y を計算に含める為、target leakageがおこり、過学習する可能性があるのです。
その為、CatBoostでは TSの時と同様に、online machine learning のアルゴリズムを使うことで、限られたデータサイズでも、target leakageを制御することができるのです。この勾配法は Ordered Boostingと呼ばれています。
以下が、ordered boosting を使った木の構築のアルゴリズムです。
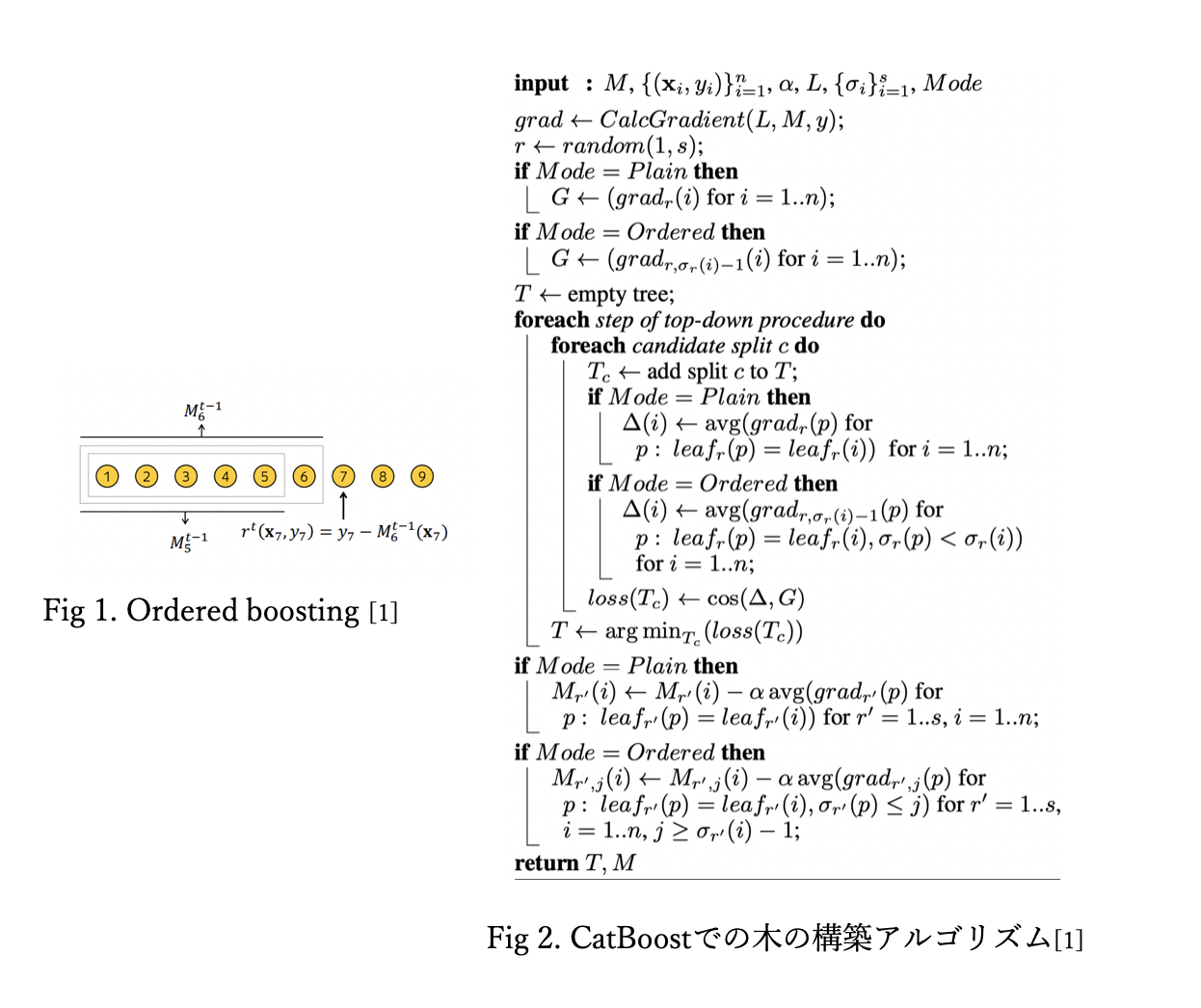
3. 特徴量の組み合わせ
複数の特徴量間に多重共線性がある場合、それらの特徴量の傾向に強く影響されてしまいます。その為、CatBoostでは、複数のカテゴリカル変数を組み合わせ、新たな特徴量を作りTSを計算し、モデルに組み込みます。
CatBoostのパラメター
CatBoostの代表的なパラメターを紹介します。
これ以外にも様々ば便利な設定ができるので、是非一度公式ドキュメントに目を通してみてください。
| パラメター | 概要 | 値 | デフォルト |
|---|---|---|---|
| cat_features | カテゴリカル変数を明示する。 | list | None |
| text_features | テキストデータを含んだ変数を明示する。 | list | None |
| sample_weight | 各変数の重み | float list | 1 |
| group_id | グループを表す変数を明示 | list | None |
| loss_function | 学習に使われるmatric | Logloss, MultiClass, (CatBoostRegressorではRMSE) | 目的関数の値による |
| iterations | 構築する木の最大数 | int | 1000 |
| learning_rate | 学習率 | float | Logloss, MultiClass, RMSEでは自動で設定。0.03 |
| random_seed | 乱数のseed | int | None |
| l2_leaf_reg | L2正則化項の係数 | float | 3.0 |
| depth | 木の最大の深さ | int | 6 |
| subsample | 学習で使うサブサンプルの割合 | float | データの規模が100以下: 1, Poisson/Bernoulli: 0.66, MVS : 0.8 |
| random_strength | 木の構築の際のスコアリングに与えられる乱数。大きいほど過学習を防ぐ。 | float | 1 |
| one_hot_max_size | カテゴリカル変数の最大グループ数 | int | ターゲットの設定、CPU・ GPUによる |
| nan_mode | 欠損値の処理方法 | "Forbidden", "Min", "Max" | "Min" |
| boosting_type | 勾配法のアルゴリズム | "Ordered", "Plain" | データサイズによる |
PythonでCatBoostを実装
import catboost as cb
# カテゴリカル変数を指定
cat_features_index = [1,3,5,6,7,8,9,10,11]
clf = cb.CatBoostClassifier('depth': 4, 'iterations': 300, 'l2_leaf_reg': 9, 'learning_rate': 0.03)
clf.fit(train_X, train_y, cat_features= cat_features_index)
pred_y = clf.predict(test_X)
accuracy_score(pred_y,test_y)
Reference
[1] Liudmila Prokhorenkova, Gleb Gusev, Aleksandr Vorobev, Anna Veronika Dorogush, Andrey Gulin, arXiv:1706.09516v5
[2] https://catboost.ai/docs/concepts/python-quickstart.html