広告の効果測定
アナログ/デジタル
テレビ広告、交通広告などに代表される従来のアナログ広告では、限定的にしか効果測定を行なえませんでした。
例えば調査会社に依頼して想起率を定点観測するといったものでした。
限られた項目しか調査できず、かつ、調査そのものに時間及び金銭的なコストがかかるものでした。
つまり従来の広告とは、当たるも八卦当たらぬも八卦、やっていきの世界だったわけです。
時は流れて、インターネットでの消費行動が一般化していく過程で、広告手法にも革命が起こります。
デジタル化です。
デジタル広告ではGETリクエストという形で、ユーザーがどの広告を押したのかという情報を得られます。
これにより、効果測定が容易、かつ無料で可能になったのです。
さらにそれを集約した状態でビジュアライズをするGoogle Analyticsも登場しました。
このように、広告がアナログからデジタルへと進化したことを背景として、"いかに効率よく広告を出し、集客をできるか"ということが、集客戦略の大きなウェイトを占めるようになりました。
デジタル広告時代に突入したわけですね。
Livesense Analyticsと弊社の事情
弊社ではLivesense AnalyticsというプライベートDMPを自社開発しており、ユーザーデータの収集に注力しております。
弊社の所有するサービスのデータはもちろん、ユーザーの行動ログや広告運用の結果を収集しております。
これをAmazon Redshift上に貯蔵しており、個人情報以外は誰でもいつでも閲覧が可能です。
Livesense Analyticsに一度SQLを打てば、”誰が、いつ、どこで、何をしたのか、そして彼はどこから来たのか、それにいくら費用がかかったのか、そしてどういう結果に至ったのか”というミクロなローデータと、それを集約した定量データを得られるのです。
ということは、最適なROI(Return On Investment = 費用対効果)を把握した上で広告投下をすることができるのです。
デジタル広告時代においては、
1.データを収集する
2.集約し分析する
3.意思決定を行う
というデータドリブンマーケを、どれだけの精度でできるかが競争優位に繋がっていきます。
ここの領域の完成度と注力度において弊社は日本随一かもしれません。
弊社での働き方に関心がある人は、こちらから是非エントリーお願いします!
利益最大化のための広告運用
運用スタイル
すみません、宣伝で脱線しました。
さてさて、広告運用にはいろいろなスタイルがあります。
例えば、とにかくインプレッションを出すという体育会系なものや、予算内でコンバージョン数を最大化するものなど様々なものがあります。
弊社では基本的に利益最大化が好まれます。(特に成熟サービスでは)
利益最大化における広告運用においては下記のAとBの運用パターンだとBのほうが好まれます。
| 運用パターン | 売上 | 費用 | 利益 |
|---|---|---|---|
| A | 1億円 | 9000万円 | 1000万円 |
| B | 2000万円 | 500万円 | 1500万円 |
つまり、利益の絶対額が高くなるような広告運用を行う必要があるということですね。
さて、次にAとBのそれぞれのROIを算出してみましょう。
単純に売上/費用で出せばいいので、下記のようになります。
*注 この記事ではROIをROASと同じ定義で使ってます。
| 運用パターン | 売上 | 費用 | 利益 | ROI |
|---|---|---|---|---|
| A | 1億円 | 9000万円 | 1000万円 | 111.11% |
| B | 2000万円 | 500万円 | 1500万円 | 400.00% |
パターンBはすごいですね。費用の4倍もの売上を叩き出してます。
このような数字を見ると、一見”ROIが高くなるように運用すれば自然に利益は最大化される”といったような誤った結論を下しがちです。
しかしながら、ROIは、"高ければ高いほどよい"というものではありません。
例えばパターンCはどうでしょう。
ROI300%で、パターンBよりもROIは低いですが、利益は最大となってます。
| 運用パターン | 売上 | 費用 | 利益 | ROI |
|---|---|---|---|---|
| A | 1億円 | 9000万円 | 1000万円 | 111.11% |
| B | 2000万円 | 500万円 | 1500万円 | 400.00% |
| C | 3000万円 | 1000万円 | 2000万円 | 300.00% |
オークションとROI
実は、デジタル広告は基本的にオークションなので、ROIを高めるほど、入札単価は低くなります。
(ここでは説明を簡略化するためにCPA, CTRといった概念は省略します。)
その結果、入札負けしてしまい、広告配信機会を逃してしまいます。
つまりROIを高めるほど、機会損失が発生してしまうわけですね。
利益最大化となるROI
前提
さて本題です。
ではROIが一体何%なら利益は最大化されるのでしょうか。
ここに以下のような過去実績があるとします。
| 売上 | 費用 | 利益 | ROI |
|---|---|---|---|
| 1億円 | 1億円 | 0円 | 100.00% |
| 8000万円 | 6700万円 | 1300万円 | 120.00% |
| 7000万円 | 5400万円 | 1600万円 | 130.00% |
| 5000万円 | 3300万円 | 1700万円 | 150.00% |
| 3000万円 | 1800万円 | 1200万円 | 170.00% |
| 2000万円 | 1100万円 | 900万円 | 180.00% |
| 1000万円 | 500万円 | 500万円 | 200.00% |
この表だけみると、ROI150%で運用すれば利益額最大になるように思えます。
しかし過去データにない、ROI140%とか160%のほうが結果が良いかもしれません。
この最適値を探るためにPythonを用いて微分を行います。
グラフ生成
まずは、X軸にROI, Y軸に利益額(百万円)を打ったグラフを生成します。
import numpy as np
import matplotlib.pyplot as plt
x= np.asarray([1, 1.2, 1.3, 1.5, 1.7, 1.8, 2])
y= np.asarray([0, 13, 16, 17,12, 9 , 5])
plt.plot(x,y,'o')
plt.grid(True)

グラフができました。
フィッティング
次にフィッティングを行います。1次元から4次元までを試します。
以下の式はこちらのブログ上のものを参考にさせていただきました。
xp = np.linspace(1, 2, 100)
for i in range(4):
p4 = np.polyfit(x, y, i+1)
p = np.poly1d(p4)
plt.scatter(x,y)
#多項式回帰線
plt.plot(xp, p(xp), c='r')
plt.title('deg = {}'.format(i+1))
plt.show()

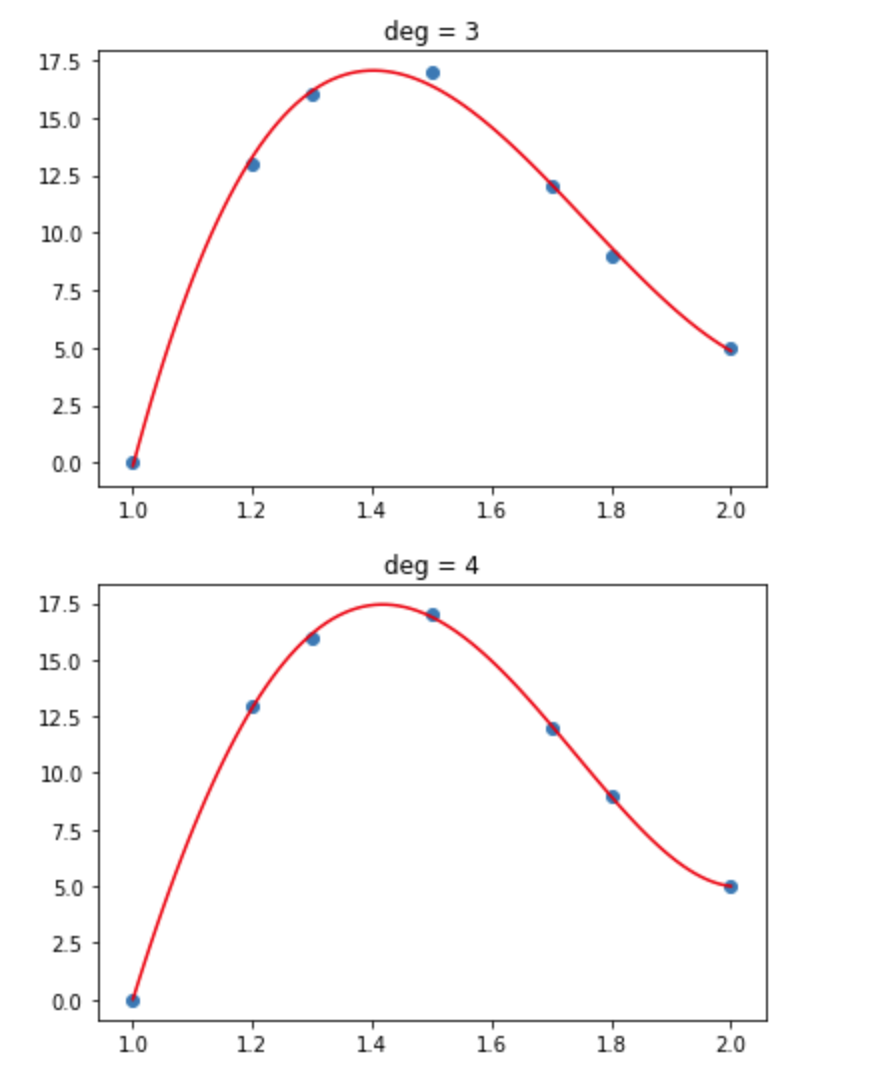
4次元でほぼ正確にグラフを描画できているので4次元を採用します。
微分による極大値の算出
4次元のときの方程式をチェックします。すると下記の式になることがわかりました。
p = np.poly1d(p4)
print(p)
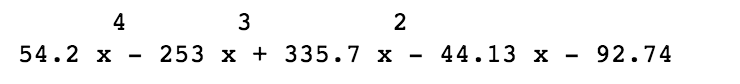
あとはこの値の微分して、極大値を求めれば、グラフの頂点がわかります。
その頂点こそが、利益最大化となるROIとなります。
import sympy
x = sympy.Symbol('x')
expr = p4[0] * x ** 4 + p4[1] * x ** 3 + p4[2] * x ** 2 + p4[3] * x + p4[4]
# sympy.diff()で微分できる。
derivative = sympy.diff(expr, x)
# sympyのplottingを使って導関数をグラフ化する。
sympy.plotting.plot(derivative, (x, 1, 2))
# 極値を求める。
results = sympy.solve(derivative)
for result in results:
result = round(result, 3)
# 極大値が存在する1.2から1.8の中から極値を抽出する。
if 1.2 < result < 1.8:
print(result)
maximum_value = result
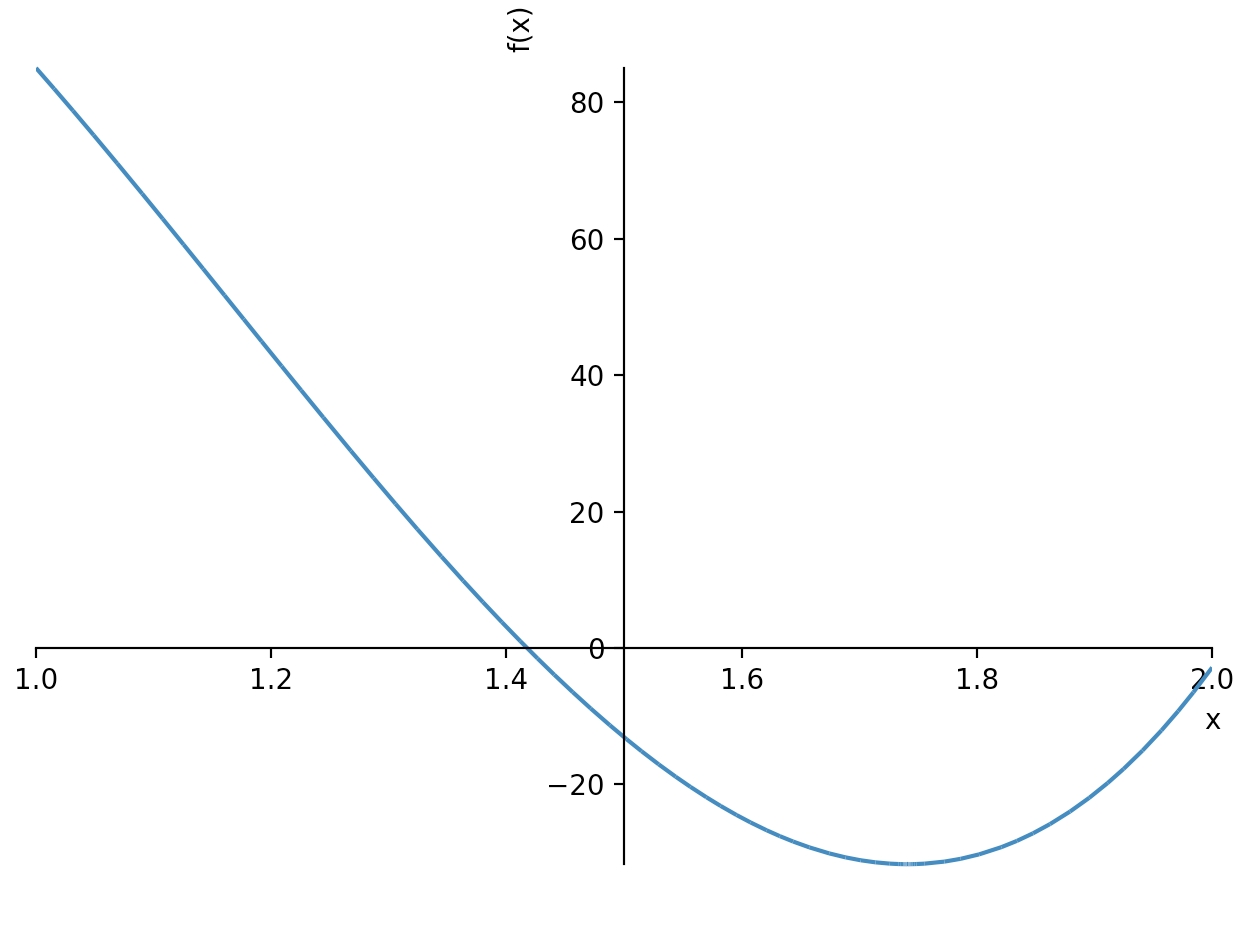
解答は1.418となります。
すなわち141.8%で広告運用を行えば、利益最大化となります。
グラフでも1.418のときのに変化量が0になってますよね。
その際の利益額は下記で算出します。
expr.subs([(x, maximum_value)])
解答は1743万円となります。
結論
下記過去データを用いて、利益最大化となるROIを算出すると141%となる。
さらにその時の利益額は1740万円である。
| 売上 | 費用 | 利益 | ROI |
|---|---|---|---|
| 1億円 | 1億円 | 0円 | 100.00% |
| 8000万円 | 6700万円 | 1300万円 | 120.00% |
| 7000万円 | 5400万円 | 1600万円 | 130.00% |
| 5000万円 | 3300万円 | 1700万円 | 150.00% |
| 3000万円 | 1800万円 | 1200万円 | 170.00% |
| 2000万円 | 1100万円 | 900万円 | 180.00% |
| 1000万円 | 500万円 | 500万円 | 200.00% |
ちなみに
numpyとmatplotを用いれば、先程の式においてxを0.01単位で動かした場合のグラフを描画できます。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1, 2.0, 0.01)
y = p4[0] * x ** 4 + p4[1] * x ** 3 + p4[2] * x ** 2 + p4[3] * x + p4[4]
plt.plot(x, y)
plt.show()
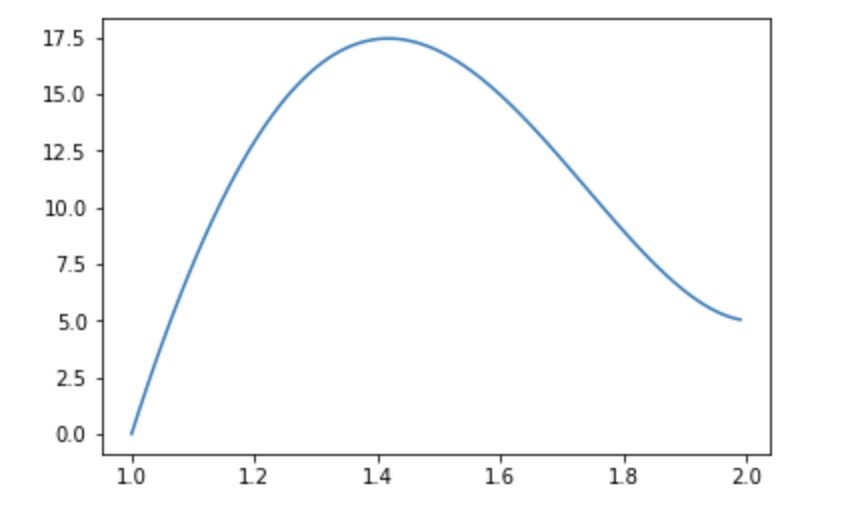
きれいなグラフですね!