初めに
またdigitsネタ、一回目はこちら。同じデータをいろいろな方法を使用して、ごちゃごちゃ分析するのはデータ分析の基本中の基本(?)なので…。
Random Forestは、パラメータの寄与率まで出せるという利点があります。今回はdigitsをRandom Forestで学習させてみて、一回目で分析したPCAと比較していきたいと思います。
Random Forestを使ってみる
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn import ensemble
from sklearn import metrics
from sklearn import decomposition
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
digits = datasets.load_digits()
# 画像データとtargetデータを取得
data,target = digits["data"],digits["target"]
data /=16
# テストデータを0.75,0.25に分割
data_train,data_test,target_train,target_test =\
train_test_split(data,target,test_size=0.25, random_state=0)
# random forest
clf = ensemble.RandomForestClassifier()
clf.fit(data_train,target_train)
predict = clf.predict(data_test)
print("accuracy_score:", metrics.accuracy_score(predict,target_test))
accuracy_score: 0.9511111111111111
特にパラメータチューニングを行っていませんが、それなりの正答率ではないでしょうか?
sklearnは機械学習のアルゴリズムが変化しても、同じ書き方ができるので使いやすいですね。
次にRandom Forestで変数毎に特徴量を出してみます。
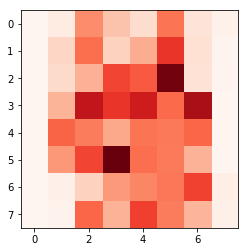
plt.imshow(clf.feature_importances_.reshape(8,8),cmap=plt.cm.Reds)
plt.show()
「clf.feature_importances_」でそれぞれの特徴量の重要度を出すことができます。digitsが64次元の画像データなので、clf.feature_importances_も64次元の数字が排出されます。
そのままですと分かりにくいので、reshapeして8×8の2次元配列に直し、画像データとして可視化しました。
濃い赤の場所が寄与率が高い場所。すなわちRandom Forestが画像を見分けるのに使用した場所になります。一番左の行と右の行は存在してもしなくても、機械学習的には必要ないデータということになります。
主成分分析
次に主成分分析を使って、第一主成分に使用されている変数を見ていきたいと思います。
# 主成分分析
pca = decomposition.PCA(n_components=1)
pca.fit_transform(data)
# 主成分の変数のヒストグラムをとる
plt.hist(pca.components_.T, bins=15)
plt.xlim(-0.4,0.4)
plt.show()
pca.components_で変数を出力することができます。しかしながら、pca.components_ではデータのサイズが(1,64)になってしまっているので、「.T」で転置させてヒストグラムを描画しています。ヒストグラムは
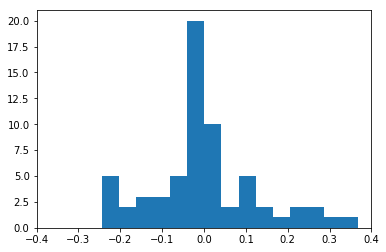
となります。0付近の変数は主成分にあまり含まれていない変数で、0から離れるほど、主成分中に多く含まれている変数となります。
主成分に含まれている変数を可視化すると
# 主成分の変数の絶対値をreshapeして、8×8にする
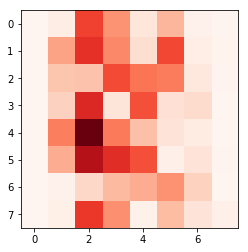
plt.imshow(np.abs(pca.components_.reshape(8,8)),cmap=plt.cm.Reds)
plt.show()
結果は
一番濃い赤の部分で0.3ぐらい。例えば一番左上の画素では4.9e-17ぐらいで、その差は歴然としています。
random forestと同様に一番左端と右端がほとんど寄与していないという結果がえられました。
第一主成分だけなので、第二主成分、第三主成分まで考えるとまた結果は変わって来るかもしれませんが、ざっと数字を確認してみたところ、やっぱり一番左端と右端はほとんど含まれていませんでした。