序論
アナログ信号をデジタル信号に変換するとき、サンプリング周波数$f_s$の1/2の大きさの周波数までしか、観測することが出来ません。
この周波数をナイキスト周波数と呼びますが、このナイキスト周波数を超えた振動は低周波数として処理されます。
ナイキスト周波数を超えた高周波数の振動を低周波数として処理してしまうことをエイリアシング(折り返し雑音)と呼びます。
$x_0$から$x_{N-1}$までの$N$個の数字を持つデータの離散フーリエ変換を考えると、
C_k = \frac{1}{N}\sum_{m=0}^{N-1} x_me^{-i\frac{2\pi km}{N}}
k = 0, 1, 2, …, N-1
kに対応する周波数は
f_k = \frac{kf_s}{N}
となります。
$k$は$(N-1)$まで存在するので,$f_{N-1}=\frac{(N-1)f_s}{N}$となり、$f_s/2$のナイキスト周波数を超える振動まで表現出来そうですが…,$C_k$と$C_{N-k}$は互いに共役な複素数であることが知られています。
C_k = C_{N-k}^*
そのため,$f_s/2$を中央として、折り返しが発生します。誤解を恐れずに言うと、$C_{N-k}$の周波数に該当する波は$C_k$の周波数の波として処理されてしまいます。
画像生成
numpyを使って、高解像度の画像(5000×5000)を生成します。これを擬似的にアナログの信号と見なします。
import numpy as np
import matplotlib.pyplot as plt
# 画像のサイズを指定
img_size_origin = 5000
# 画像として零行列
img = np.zeros([img_size_origin, img_size_origin])
# 画像の画素の値はy座標に依存
y = np.arange(img_size_origin)
# 周期100画素
amp = np.sin(2*np.pi*0.01*y)
for i in range(img_size_origin):
img[:, i] = amp
plt.imshow(img, cmap="gray")
plt.show()
これにより50個の縞模様を持つ画像が生成されます。
50個の縞模様を持つので、画像全体を1周期と見なすと50 Hzの波が存在していることになります。
この画像より[comp×comp]につき1ピクセルだけ抜き出して、新たな画像を生成します。
comp = 5 の場合, 抜き出すピクセルは[3 + 5n, 3 + 5m]の座標になります。(n>=0, m>=0)
comp = 99
# 出力の画像サイズを計算
img_size = img.shape[0]//comp
# 出力の画像
img_comp = np.zeros([img_size, img_size])
# [comp×comp]の画素のうち、中央の画素のみを抜き出し
for i in range(img_size):
for j in range(img_size):
img_comp[i, j] = img[(i*comp) + (comp//2), (j*comp) + (comp//2)]
plt.imshow(img_comp, cmap="gray")
plt.show()
plt.plot(img_comp[:, 0])
plt.show()
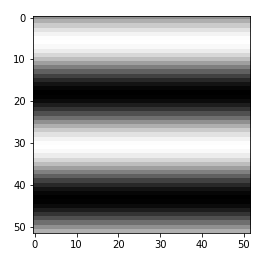
compが99の場合
50 Hzの波をうまく観測出来ず, 0.5 Hzの波になってしまいました。


compが98の場合
50 Hzの波をうまく観測出来ず, 1 Hzの波になってしまいました。


compが96の場合
50 Hzの波をうまく観測出来ず, 2 Hzの波になってしまいました。
終わりに
不思議画像がたくさん出来そう(小並感)