【ベクトル・行列】行列の出来るベクトル入門

はじめに

スキルアップAI株式会社が無料提供するデータサイエンティスト基礎講座のベクトル節がとてもわかり易かったので、自分的解釈も含めてまとめます。以下の項目についてまとめました

• ベクトル（Vector）:とは数字を並べたもの
• スカラー（Scalar）:ベクトル内の数字や単一の数
• ベクトルの次元（Dimension）：ベクトル内のスカラーの数
• ノルム（Norm）：ベクトルの長さを計る指標
• 行列（Matrix）：数字を2次元に並べた物
• 正方行列（Square Matrix）：列と行の数が等しい行列
• 単位行列（Identity Matrix)：平方行列かつ対角成分が全て1でそれ以外が0の行列の事を指し、行列の世界では1のような役割を持つ
• 逆行列（Inverse Matrix）$A^{-1}$：行列の世界に置ける対数のような物
• 正則行列（Regular Matrix）：逆行列が存在する行列
• 行列式（Determinant）|A|：逆行列の散財有無を確認する式　算出した値が０になる時、その行列には逆行列が存在しない事を意味する
• 転置行列（Transposed Matrix）$\textit{A}^\intercal$：とは、行列の行と列を入れ替えてできる行列
• 線形変換（Linear Transformation）：ベクトルに行列をかける事でベクトルの向きと長さを変える事
• 固有ベクトル（Eigenvector）：線形変換を行なった際に矢印の方向は変わらず、伸縮だけが変わるベクトル
• 固有値（Eigenvalue）：固有ベクトルにおける伸縮率

ベクトル（Vector）とは

ベクトル（Vector）とは数字を並べたもの。ベクトル内の数字の数をスカラー（Scalar）と言い、その数をベクトルの次元（Dimension）と言います。ベクトルには縦ベクトルと横ベクトルの２種類あり、行列（Matrix）を考える際に重要になってきます。
例えば、4次元の縦ベクトルxは以下の様に表されます。

$$
\boldsymbol{x} =
\begin{bmatrix}
\epsilon_1 \\
\epsilon_2 \\
\vdots \\
\epsilon_N \\
\end{bmatrix}
$$

ベクトルの考え方

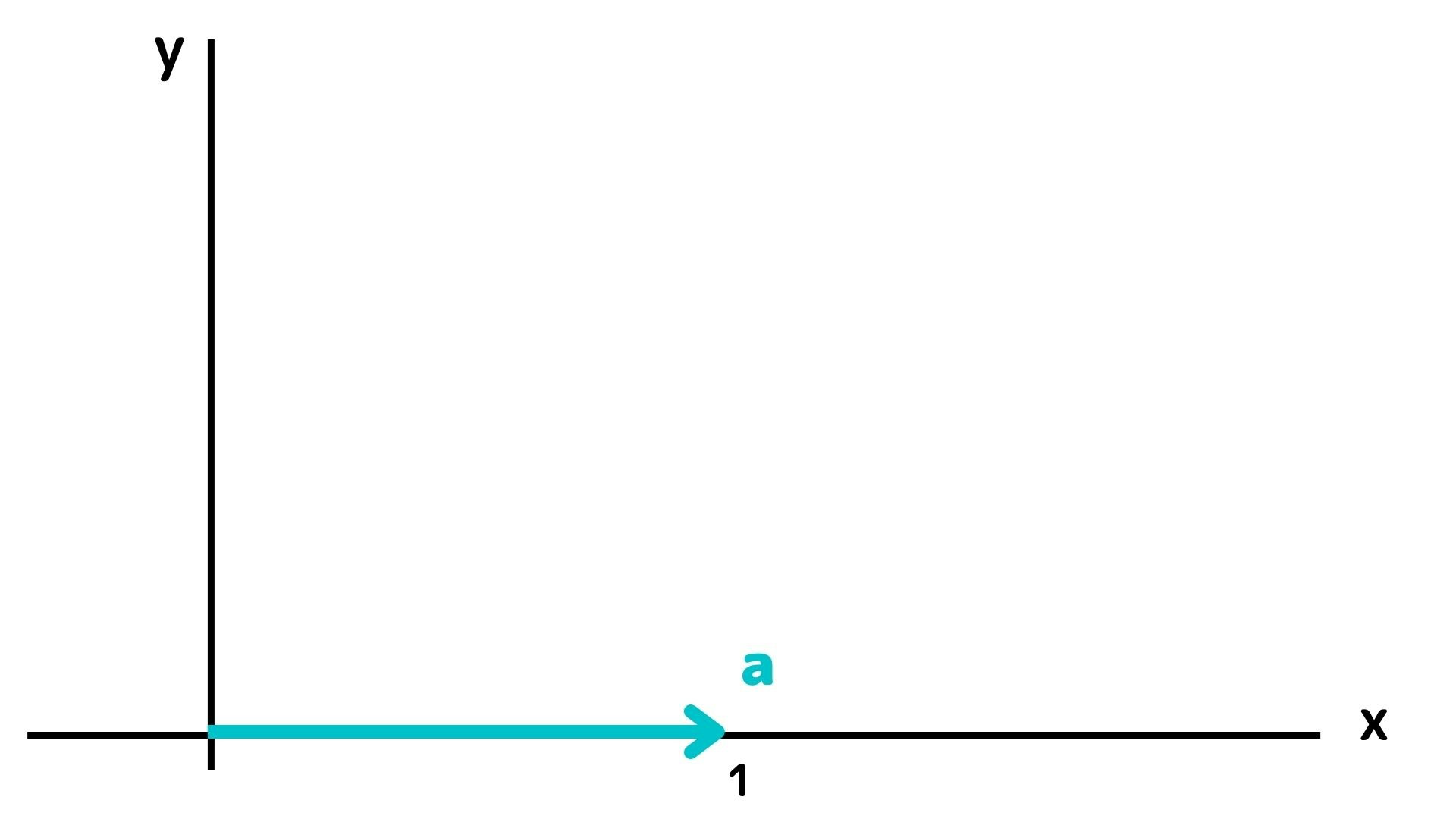
ベクトルの中にある数値の数を次元と言います。数学のxとyの図を思い浮かべるとイメージしやすいです。図に1次元とはx軸しか無い状態の事を指し、2次元になるとそこにy軸が加わります。同じように3次元になるとz軸が加わり、図自体の次元も上がっていきます。例えば、2次元のベクトルaは以下のようなイメージで考えられます。
$$
\boldsymbol{a} =
\begin{bmatrix}
1\\
0\\
\end{bmatrix}
$$

和

ベクトルの足し算は次元が同じ場合は成分ごとの足し算で表されます。
$$
\boldsymbol{a} =
\begin{bmatrix}
1\\
0\\
\end{bmatrix}
\quad
\boldsymbol{b} =
\begin{bmatrix}
0\\
1\\
\end{bmatrix}
$$
の場合
$$
\boldsymbol{a}+\boldsymbol{b}=
\begin{bmatrix}
1\\
0\\
\end{bmatrix}
+
\begin{bmatrix}
0\\
1\\
\end{bmatrix} =
\begin{bmatrix}
1 & 0\\
0 & 1\\
\end{bmatrix} =
\begin{bmatrix}
1\\
1\\
\end{bmatrix}
$$
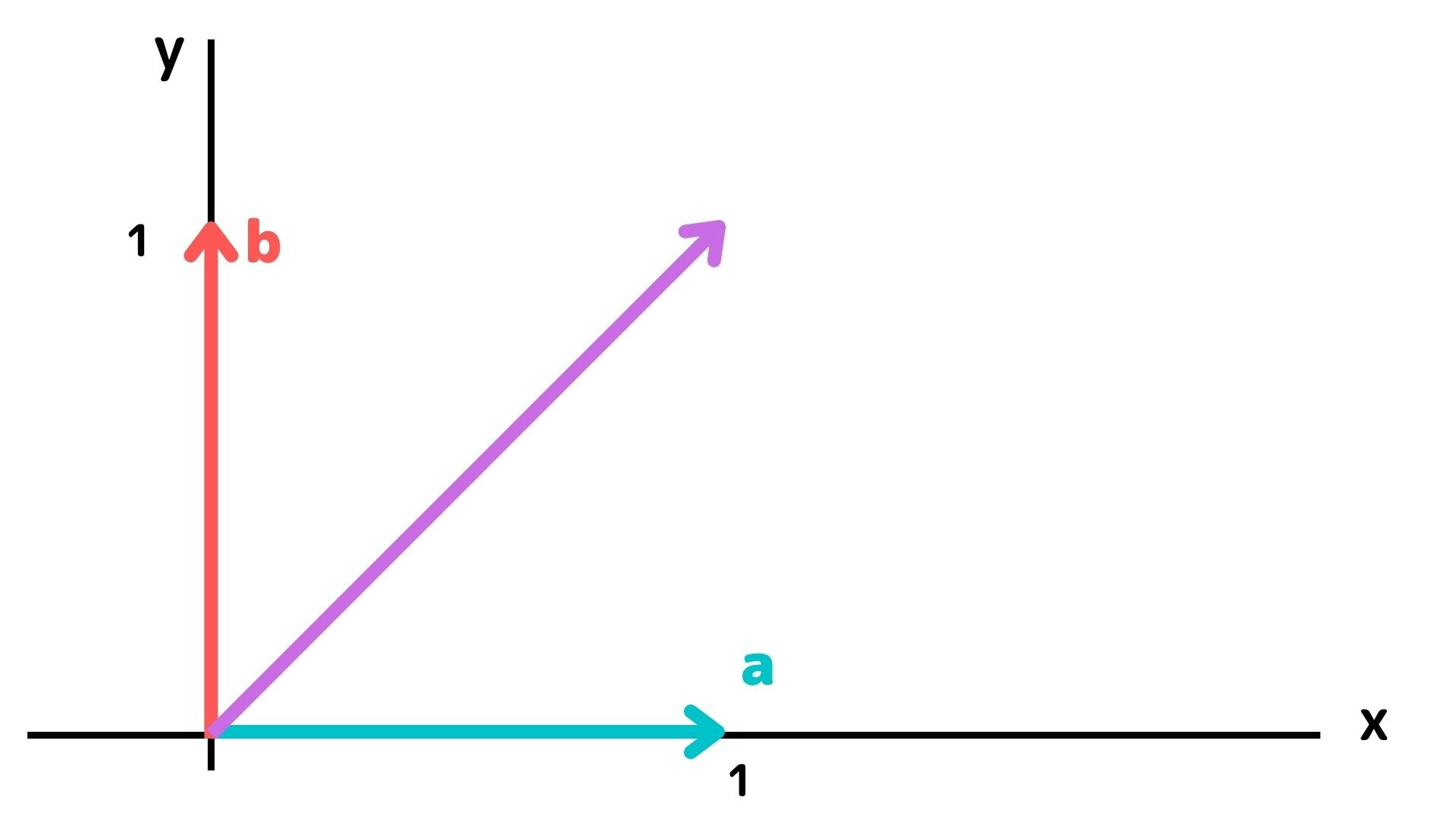
となり、解のベクトルは紫の矢印の様に表されます。

スカラー倍（Scalar Multiplication）

スカラー倍をとると、矢印の長さを変える処理を行います。
$$
c\boldsymbol{x}=
\begin{bmatrix}
cx_{1}\\
cx_{2}\\
\vdots\\
cx_{n}\\
\end{bmatrix}
$$
先程のベクターを2スカラー倍すると緑の矢印のように表現されます
$$
c\boldsymbol{x}=
\begin{bmatrix}
cx_{1}\\
cx_{2}\\
\end{bmatrix} =
\begin{bmatrix}
2\centerdot 1\\
2\centerdot 1\\
\end{bmatrix} = \begin{bmatrix}
2\\
2\\
\end{bmatrix}
$$

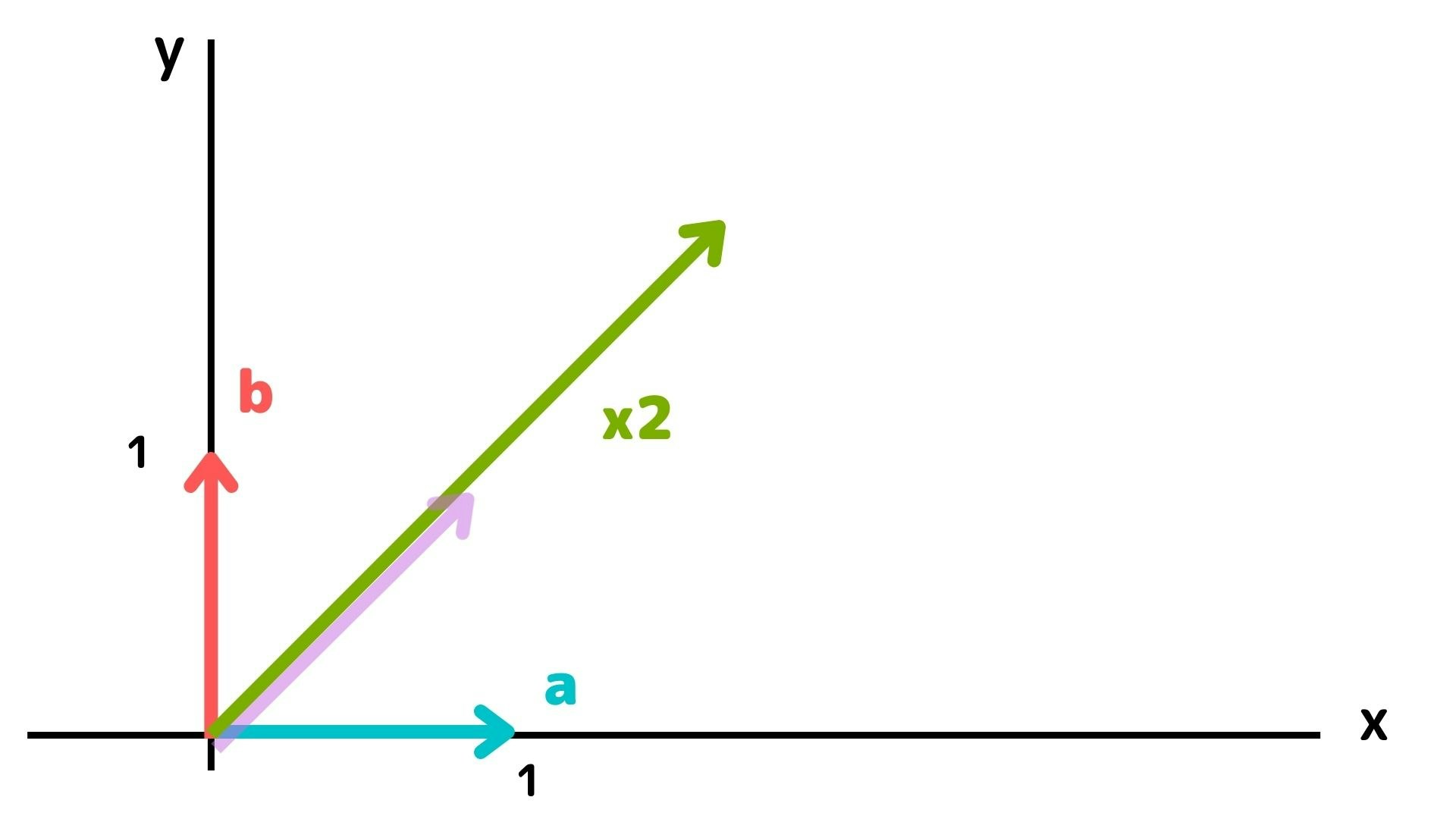
ノルム（Norm）

ノルム（Norm）とは、ベクトルの長さを計る指標です。 ベクトルxのノルムは以下の様に表されます。
$$
\boldsymbol{x} =
\begin{bmatrix}
1\\
1\\
\end{bmatrix}
$$
の時ノルム（||x||）は

$$
||\boldsymbol{x}|| = \sqrt{1^2+1^2} = \sqrt{2}
$$

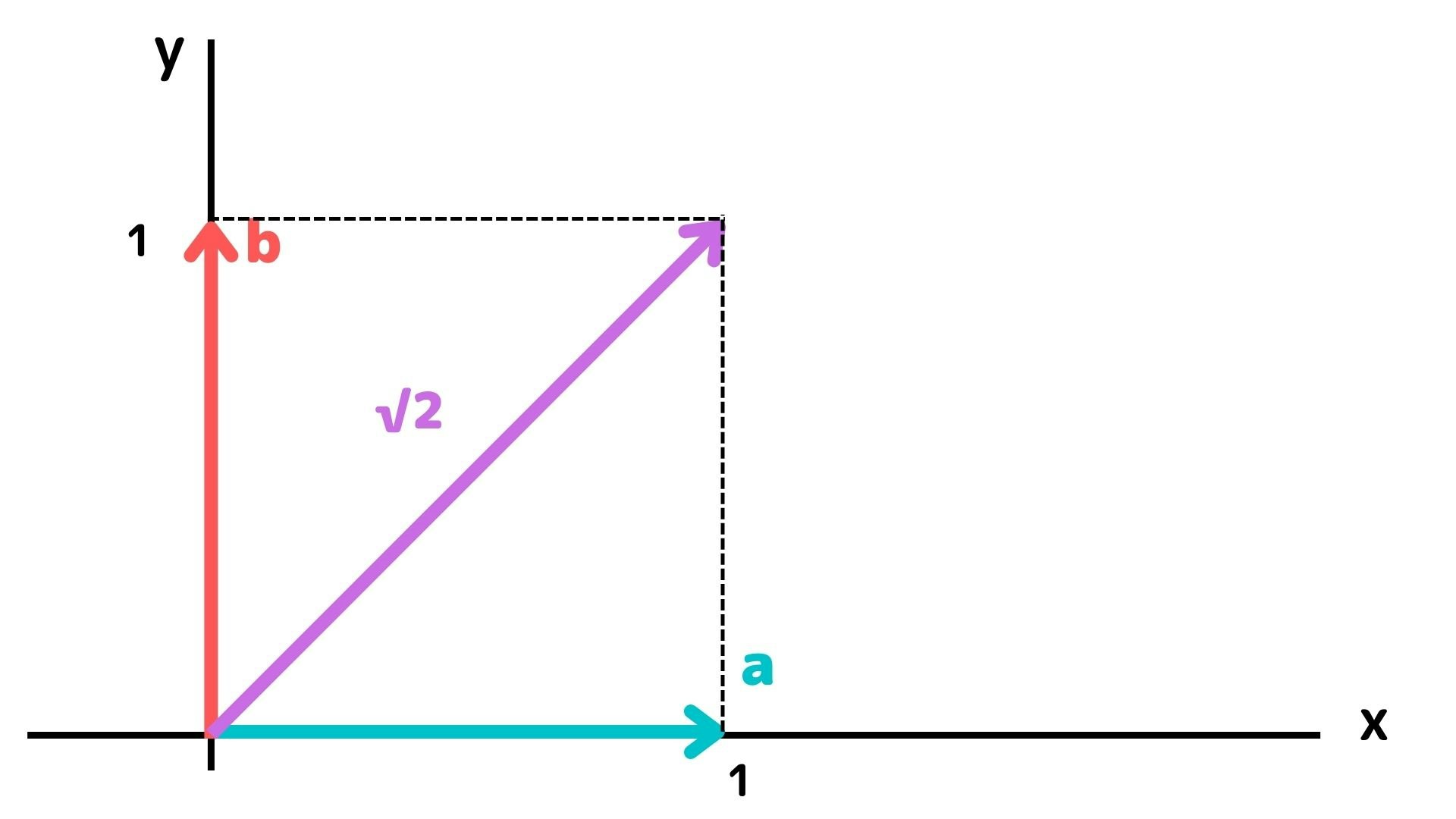
となり、$||\boldsymbol{x}|| = \sqrt{x^2_{1}+x^2_{2}} = \sqrt{2}$ を満たす$x_1,x_2$は以下の様に表せます。

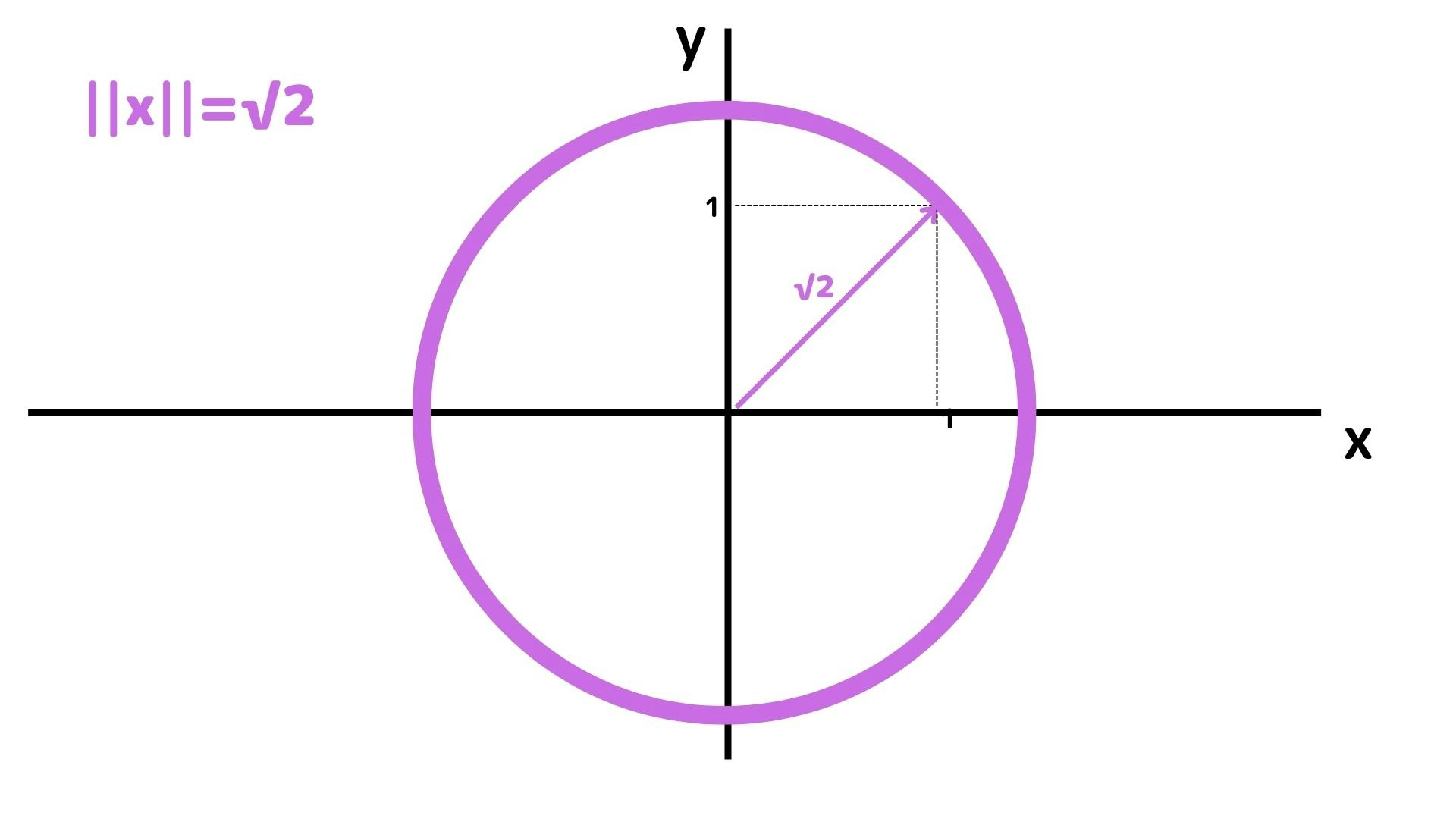
内積（Inner Product）

ベクトル同士の席を求める際、以下の様になります。
$$
\boldsymbol{x}=
\begin{bmatrix}
1\\
2\\
3\\
\end{bmatrix} \quad \boldsymbol{y}=
\begin{bmatrix}
4\\
5\\
6\\
\end{bmatrix}
$$
の場合、
$$
\boldsymbol{x}\centerdot\boldsymbol{y}=\begin{bmatrix}
1\\
2\\
3\\
\end{bmatrix} \centerdot \begin{bmatrix}
4\\
5\\
6\\
\end{bmatrix} = 1 \centerdot 4 + 2 \centerdot 5 + 3 \centerdot 6 = 32
$$

行列(Matrix)

行列(Matrix)とは、数字を2次元に並べた物です。 また、列と行の数が等しい行列を 正方行列(Square Matrix） とお呼びます。
$$
\boldsymbol{A}=
\begin{bmatrix}
a_{1,1} & a_{1,2}& \dots & a_{1,n} \\
a_{2,1} &a_{2,2}&\dots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \dots & a_{m ,n} \\
\end{bmatrix}
$$
また、単位行列(Identity Matrix)とは平方行列かつ対角成分が全て1でそれ以外が0の行列の事を指し、行列の世界では1のような役割を持ちます。
$$
\boldsymbol{E}=
\begin{bmatrix}
1 & 0& \dots & 0 \\
0 &1&\dots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \dots & 1 \\
\end{bmatrix}
$$

和

行列の和はベクトルの処理と似ていて、以下の様になります。
$$
\textit{A}=
\begin{bmatrix}
1 & 2& 3 \\
-5 & 4 & 0 \\
0 & 1 & 2 \\
\end{bmatrix} \quad
\textit{B}=
\begin{bmatrix}
6 & -3& -2 \\
5 & -6 & 7 \\
9 & -1 & 0 \\
\end{bmatrix}
$$の時

$$
\textit{A} + \textit{B}= \begin{bmatrix}
1+6 & 2-3& 3-2 \\
-5+5 & 4-6 & 0+7 \\
0+9 & 1-1 & 2+0 \\
\end{bmatrix} = \begin{bmatrix}
7 & -1 & 1 \\
0 & -2 & 7 \\
9 & 0 & 2 \\
\end{bmatrix}
$$
となります。

スカラー倍

行列のスカラー倍もベクトルの処理と似ていて、以下の様になります。
$$
\textit{A}=
\begin{bmatrix}
1 & 2& 3 \\
-5 & 4 & 0 \\
0 & 1 & 2 \\
\end{bmatrix}
$$の時

$$
2\textit{A} =
\begin{bmatrix}
2\centerdot1 & 2\centerdot2& 2\centerdot3 \\
2\centerdot-5 & 2\centerdot4 & 2\centerdot0 \\
2\centerdot0 & 2\centerdot1 & 2\centerdot2 \\
\end{bmatrix}=
\begin{bmatrix}
2 & 4& 6 \\
-10 & 8 & 0 \\
0 & 2 & 4 \\
\end{bmatrix}
$$
となります。

積

行列の積は少しややこしく、
$$
\textit{A}=
\begin{bmatrix}
1 & 2\\
-5 & 4 \\
\end{bmatrix} \quad
\textit{B}=
\begin{bmatrix}
6 & -3\\
5 & -6\\
\end{bmatrix}
$$の時

$$
\textit{A B}=
\begin{bmatrix}
(1\centerdot6+2\centerdot5) & (1\centerdot-3+2\centerdot-6)\\
(-5\centerdot6+4\centerdot5) & (-5\centerdot-3+4\centerdot-6) \\
\end{bmatrix} \quad=
\begin{bmatrix}
16 & -15\\
-10 & -9 \\
\end{bmatrix}
$$となります

逆行列（Inverse Matrix）

逆行列（Inverse Matrix）とは、行列の世界に置ける対数のような物です。 行列Aに対しての逆行列は$A^{-1}$と表記されます。行列には逆行列が存在するものと、しないものがあり、逆行列が存在する行列を正則行列 と言います。逆行列の散財有無を確認する式を行列式と言います。行列式を用いて計算した値が０になる時、その行列には逆行列が存在しない事を意味します。
$$
\textit{A}=
\begin{bmatrix}
a & b\\
c & d \\
\end{bmatrix}
$$
の場合、行列式|A|は
$$
|A| = ad-bc
$$
となり、が逆行列は
$$
A^{-1}=\dfrac{1}{|A|} \begin{bmatrix}
d & -d\\
-c & a \\
\end{bmatrix}
$$

対数のような物と説明しましたが、以下の式が成り立ちます。
$$
\textit{A}\textit{A}^{-1} = \textit{A}^{-1} \textit{A} = \textit{E}
$$

転置行列（Transposed Matrix）

転置行列（Transposed Matrix）$\textit{A}^\intercal$とは、行列の行と列を入れ替えてできる行列の事をさします

$$
\textit{A} =
\begin{bmatrix}
a & b& c\\
d &e &f \\
\end{bmatrix} \quad
\textit{A}^\intercal =
\begin{bmatrix}
a & d\\
b & e\\
c & f\\
\end{bmatrix}
$$

固有値・固有ベクトル（Eigenvalue ​​・ Eigenvector）

固有値・固有ベクトルを説明する前に、線形変換を少し説明します。

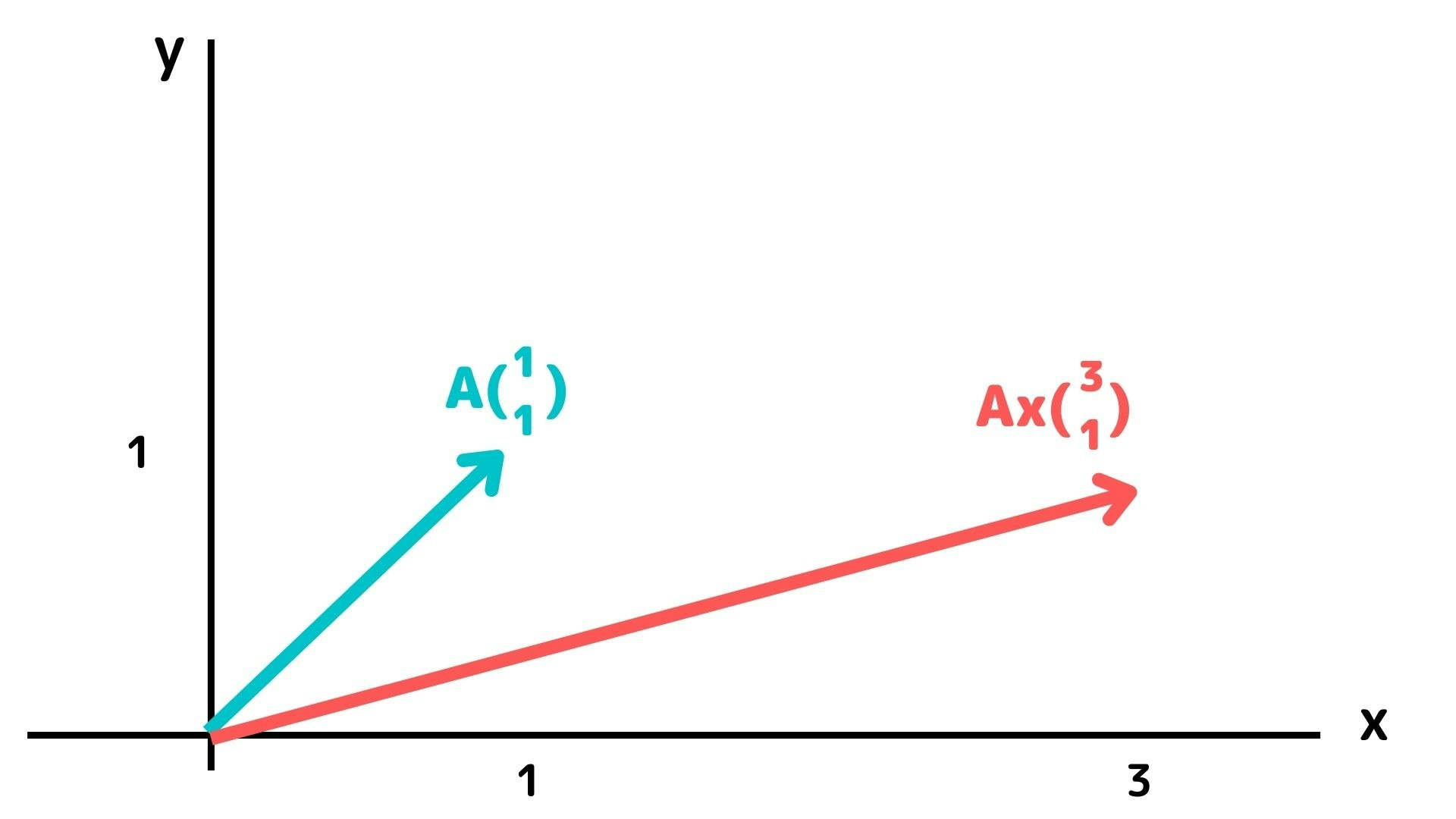
線形変換（Linear Transformation）

線形変換（Linear Transformation）とはあるベクトルに行列をかける事でベクトルの向きと長さを変える事をさします。

$
A =
\begin{bmatrix}
2 & 1\\
1 & 0\\
\end{bmatrix} \quad
\boldsymbol{x}= \begin{bmatrix}
1\\
1\\
\end{bmatrix}
$

$
A\boldsymbol{x}=
\begin{bmatrix}
2 & 1\\
1 & 0\\
\end{bmatrix}\begin{bmatrix}
1\\
1\\
\end{bmatrix} =
\begin{bmatrix}
3\\
1\\
\end{bmatrix}
$

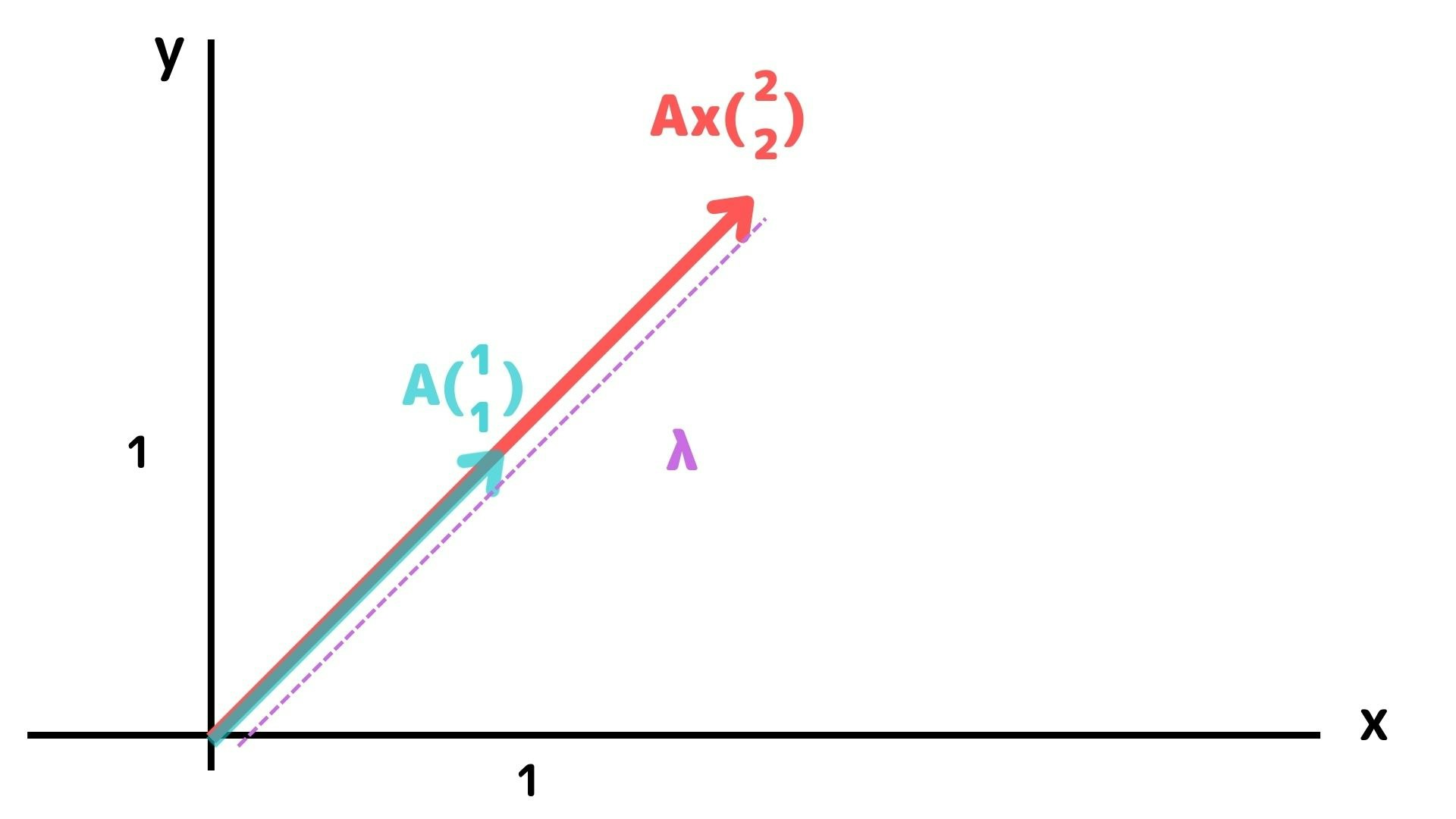
この時、行列Aをかけた際に、矢印の方向は変わらず、伸縮だけが変わるベクトルがあります。伸縮倍率を$\lambda$をした際、以下の関係が成り立ちます。
$$
A\boldsymbol{x} = \lambda\boldsymbol{x}
$$
この時の$\lambda$(伸縮率)を固有値と呼び、ベクトル$\boldsymbol{x}$を固有ベクトルと呼びます。

おわりに

• ベクトル（Vector）:とは数字を並べたもの
• スカラー（Scalar）:ベクトル内の数字や単一の数
• ベクトルの次元（Dimension）：ベクトル内のスカラーの数
• ノルム（Norm）：ベクトルの長さを計る指標
• 行列（Matrix）：数字を2次元に並べた物
• 正方行列（Square Matrix）：列と行の数が等しい行列
• 単位行列（Identity Matrix)：平方行列かつ対角成分が全て1でそれ以外が0の行列の事を指し、行列の世界では1のような役割を持つ
• 逆行列（Inverse Matrix）$A^{-1}$：行列の世界に置ける対数のような物
• 正則行列（Regular Matrix）：逆行列が存在する行列
• 行列式（Determinant）|A|：逆行列の散財有無を確認する式　算出した値が０になる時、その行列には逆行列が存在しない事を意味する
• 転置行列（Transposed Matrix）$\textit{A}^\intercal$：とは、行列の行と列を入れ替えてできる行列
• 線形変換（Linear Transformation）：ベクトルに行列をかける事でベクトルの向きと長さを変える事
• 固有ベクトル（Eigenvector）：線形変換を行なった際に矢印の方向は変わらず、伸縮だけが変わるベクトル
• 固有値（Eigenvalue）：固有ベクトルにおける伸縮率

参考文献