CPPI（Constant Proportion Portfolio Insurance）の理論とシュミレーション

はじめに

今回はポートフォリオのダイナミックバランシング戦略の一つであるCPPI（Constant Proportion Portfolio Insurance）についてご紹介します。CPPI戦略は、資産の最小価値（フロア）を保証しつつ、市場の上昇に伴いリターンを追求する方法です。この戦略の魅力と、そのシミュレーションをPythonを使ってJupyter Notebook上で実装してみた体験を共有したいと思います。

CPPIの基本概念

CPPI戦略は、投資ポートフォリオが一定のフロア値(絶対に資産をこれ以下にしないという値)を下回らないように保証しつつ、リスク資産（株式など）に積極的に投資することで高いリターンを目指す投資戦略です。投資先の資産をリスク資産とセーフ資産にわけ、リアルタイムでその比率を調整していく生産運用方法です。リスク資産とセーフ資産の差分をクッションと言い、資産家がリスク資産に投資出来る金額の基準になります。また、マルチプライヤーというレバレッジ係数をクッションに用いて、リスクアセットにどれだけ資金を割り当てるかを決定します。この係数によって、リスク資産の割合が増減し、ポートフォリオの成長機会とリスクのバランスをとります。

例えば、ポートフォリオ資産が100,000円でフロア値を80,000円に設定した場合、マルチプライヤーを3とした時。

• 初期のクッション額が　20,000円 (100,000 円 - 80,000 円 = 20,000 円)
• リスク資産への投資額　60,000円 (20,000 円 x 3 = 60,000 円)
• セーフ資産への投資額　40,000円（100,000円 - 60,000円 = 40,000円）

となります。

ここで、「ちょっと待て、マルチプレイヤーのせいですでにフロア値下回ってるぞ、ここでリスクアセットが0になったら資産がフロア値下回るぞ」 っと疑問に思った私は、この戦略のリアルタイム性の重要性に気がつきました。

リアタイムでリスク資産とセーフ資産の割合を調整し続けれられれば理論通りに資産が運用できるという事です。

そこで、「では実際どのくらいリアルタイムである必要があるのか？」そう疑問に思ってのでPythonを使って、CPPI戦略のシミュレーションを行おうと思いました。

Jupyter Notebookでのシミュレーション実装　

リスク資産のリターンを正規分布に基づいてランダムに生成し、各期間ごとにリスク資産と安全資産への割り当てを更新し、新しいポートフォリオ価値を計算します。
さらに、指定された頻度でポートフォリオのバランスを取り直します。このとき、クッションがフロアを下回った場合は、自動的にリバランスしてフロアを維持します。

import numpy as np
import matplotlib.pyplot as plt

# Simulation settings
initial_wealth = 100000  # 投資の初期資産
floor = 80000            # フロア値
multiplier = 3           # マルチプライヤー (M)
num_periods = 252        # シミュレーションの期間(日)
annual_return = 0.08     # リスク資産の予想リターン
annual_volatility = 0.20 # リスク資産のボラティリティ
risk_free_rate = 0.02    # セーフ資産のリスク利率
balance_in = 1           # 調整頻度(日)

# Generate random returns for the risky asset

np.random.seed(46)
daily_risk_return = np.random.normal(annual_return / num_periods, annual_volatility / np.sqrt(num_periods), num_periods)

# Create vectors of portfolio, safe asset, and risky asset values and give initial points
portfolio_value = np.zeros(num_periods)
portfolio_value[0] = initial_wealth

safe_asset_value = np.zeros(num_periods)
safe_asset_value[0] = initial_wealth - (initial_wealth - floor) * multiplier 

risky_asset_value = np.zeros(num_periods)
risky_asset_value[0] = (initial_wealth - floor) * multiplier 


for t in range(1, num_periods):
    
    # Allocate to risky asset based on the cushion and multiplier
    risky_allocation = risky_asset_value[t-1]
    safe_allocation = safe_asset_value[t-1]
    
    # Calculate returns
    risky_asset_return = risky_allocation * (1 + daily_risk_return[t])
    safe_asset_return = safe_allocation * (1 + risk_free_rate / num_periods)

    # Update portfolio value
    portfolio_value[t] = risky_asset_return + safe_asset_return
    risky_asset_value[t] = risky_asset_return
    safe_asset_value[t] = safe_asset_return

    # Run below code by given frequency days 
    if t % balance_in == 0:
        
        # Calculate current cushion
        cushion = max(portfolio_value[t-1] - floor, 0)
        
        # Allocate to risky asset based on the cushion and multiplier
        risky_allocation = multiplier * cushion
        safe_allocation = portfolio_value[t-1] - risky_allocation
        
        # Calculate returns
        risky_asset_return = risky_allocation * (1 + daily_risk_return[t])
        safe_asset_return = safe_allocation * (1 + risk_free_rate / num_periods)

        # Update portfolio value
        portfolio_value[t] = risky_asset_return + safe_asset_return
        risky_asset_value[t] = risky_asset_return
        safe_asset_value[t] = safe_asset_return

        # Adjust allocations if the floor is breached
        if portfolio_value[t] < floor:
            portfolio_value[t] = floor
            risky_asset_value[t] = 0
            safe_asset_value[t] = floor

# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(portfolio_value, label='Total Portfolio Value')
plt.plot(risky_asset_value, label='Risky Asset Value')
plt.plot(safe_asset_value, label='Safe Asset Value')
plt.axhline(y=floor, color='r', linestyle='--', label='Floor')
plt.title('CPPI Strategy Simulation (Balance out in every ' + str(balance_in) +' days)')
plt.xlabel('Days')
plt.ylabel('Portfolio Value')
plt.legend()
plt.show()

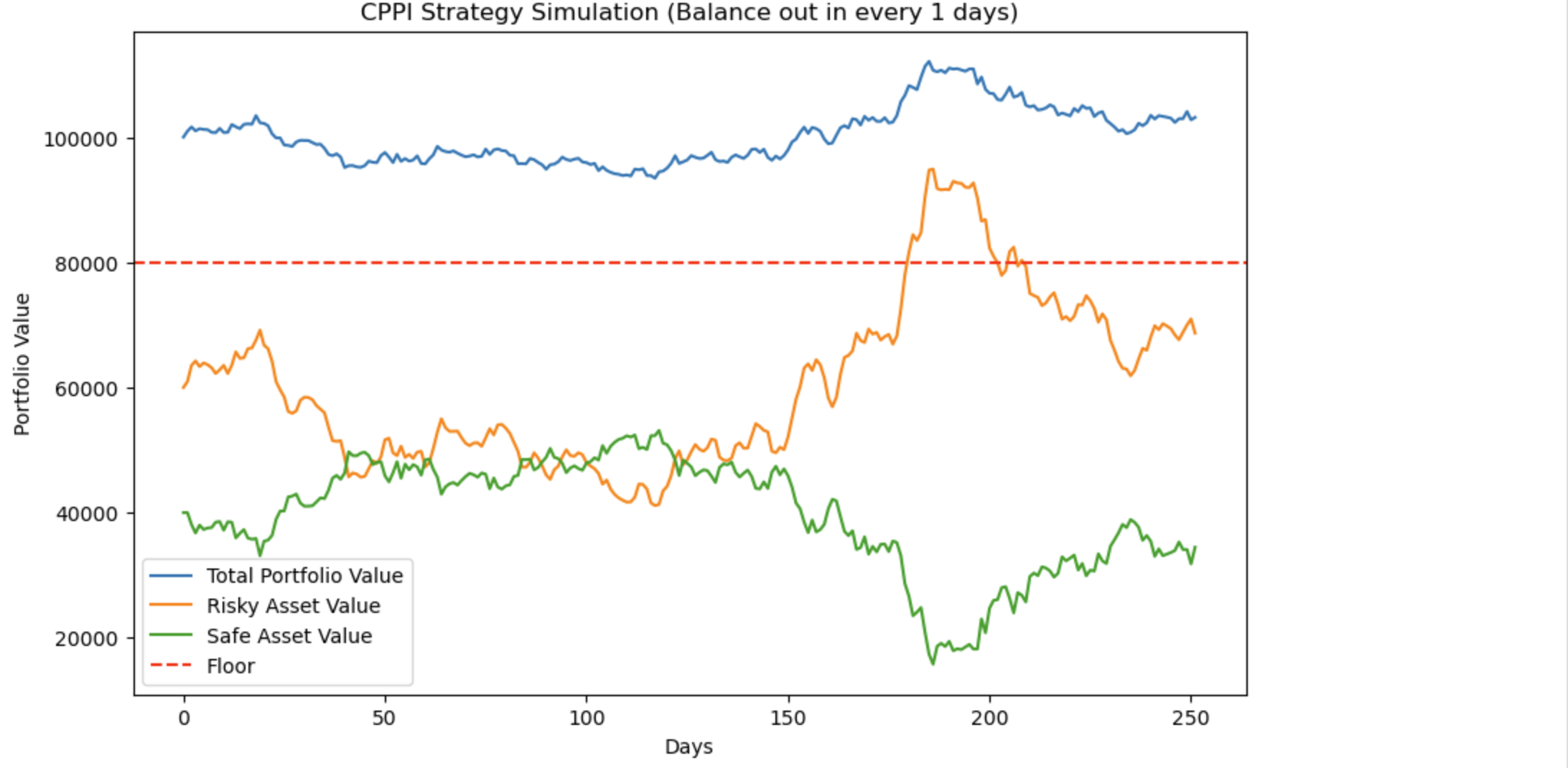
まず手始めに、理論通りリアルタイム(1日おき)に資産の割合を調整した場合をシュミレーションします。

• リスク資産の予想リターン(8%)
• リスク資産のボラティリティ(20%)
• セーフ資産のリスク利率(2%)
• 調整頻度(1日)

上記の条件でフロアを下回らずに1年間運用できてますね。序盤にリスク資産が下がった時に、クッションが減り、その分をセーフ資産に運用を切り替えて、リスク資産が上がった瞬間にクッションが増え、その分をリスク資産に投資していろ事がわかります。

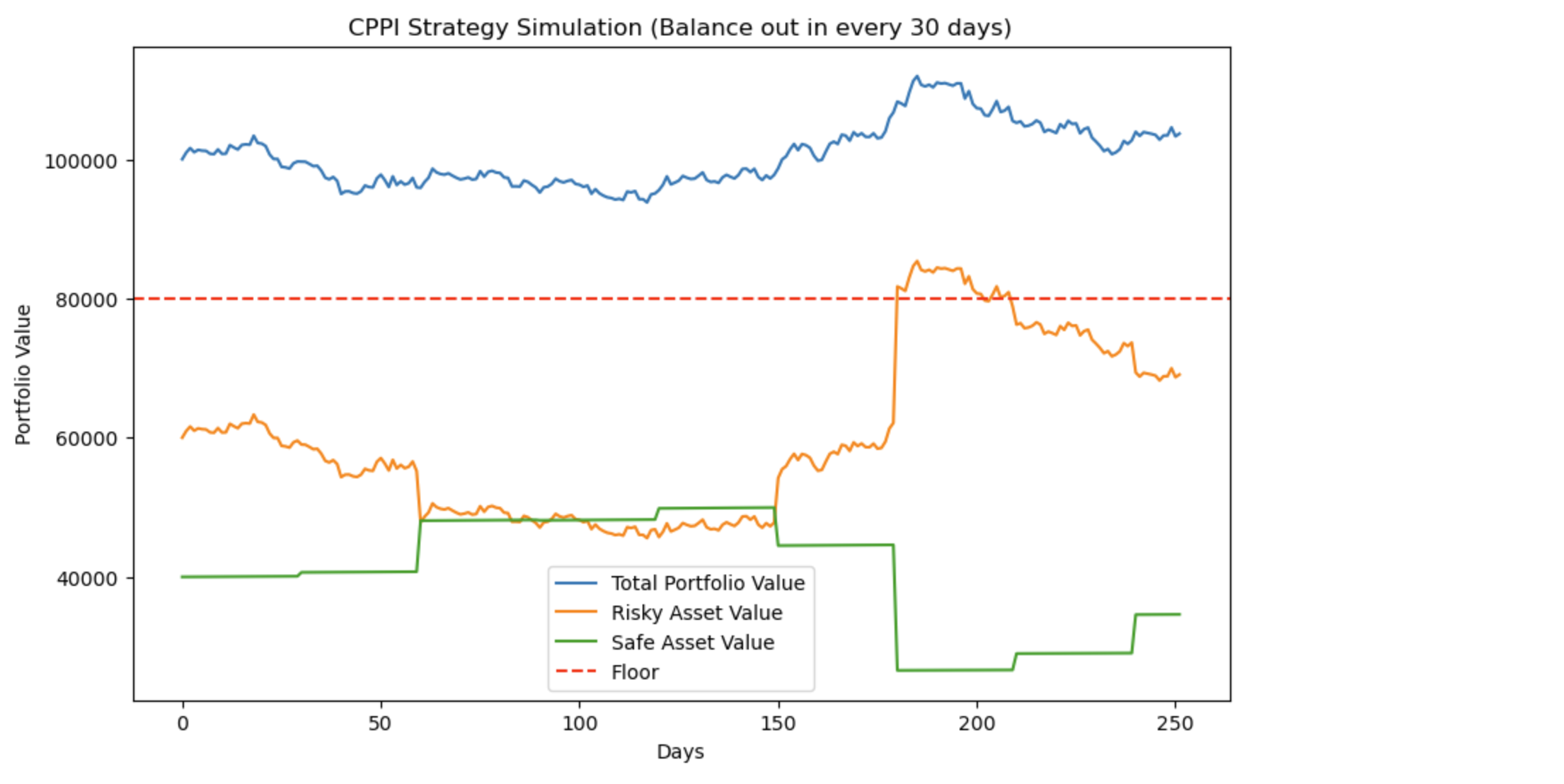
それでは30日に1回の、バランスの調整を行なった場合はどうでしょう。

• リスク資産の予想リターン(8%)
• リスク資産のボラティリティ(20%)
• セーフ資産のリスク利率(2%)
• 調整頻度(30日)

上記の条件でフロアを下回らずに1年間運用できてますね。こちらも序盤にリスク資産が下がった時に、クッションが減り、その分をセーフ資産に運用を切り替えて、リスク資産が上がった瞬間にクッションが増え、その分をリスク資産に投資していろ事がわかります。（セーフ資産の推移が30日間隔になっていますね。）

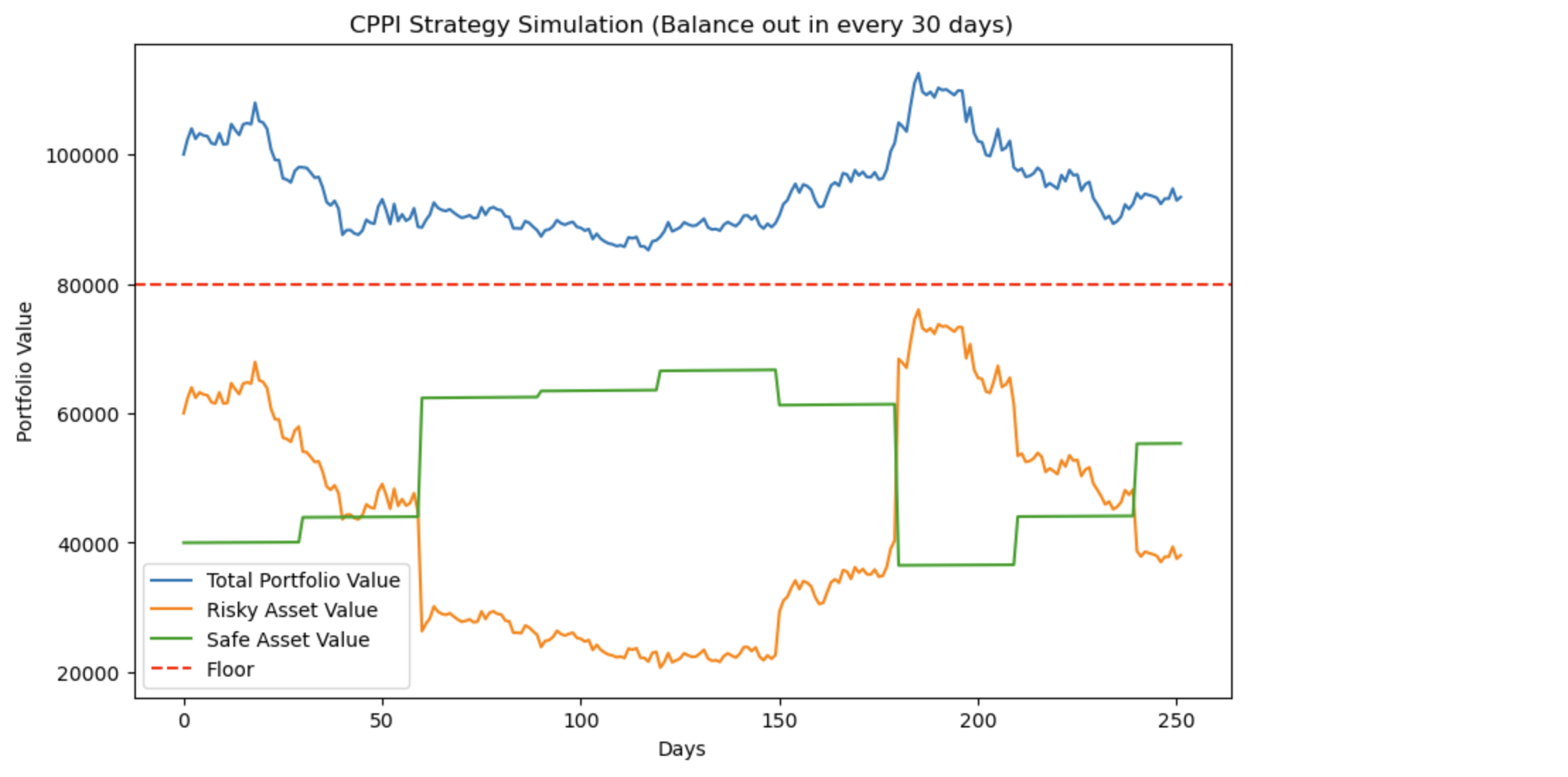
ちょっと欲を出してよりボラティリティがあるリスクアセットに投資してみましょう。

• リスク資産の予想リターン(10%)
• リスク資産のボラティリティ(50%)
• セーフ資産のリスク利率(2%)
• 調整頻度(30日)

この条件でもフロアを下回らずに1年間運用できてますね。早々にセーフ資産に割合が大きく変わっていることがわかります。このシュミレートでもフロアを下まわずに運用できていますね。

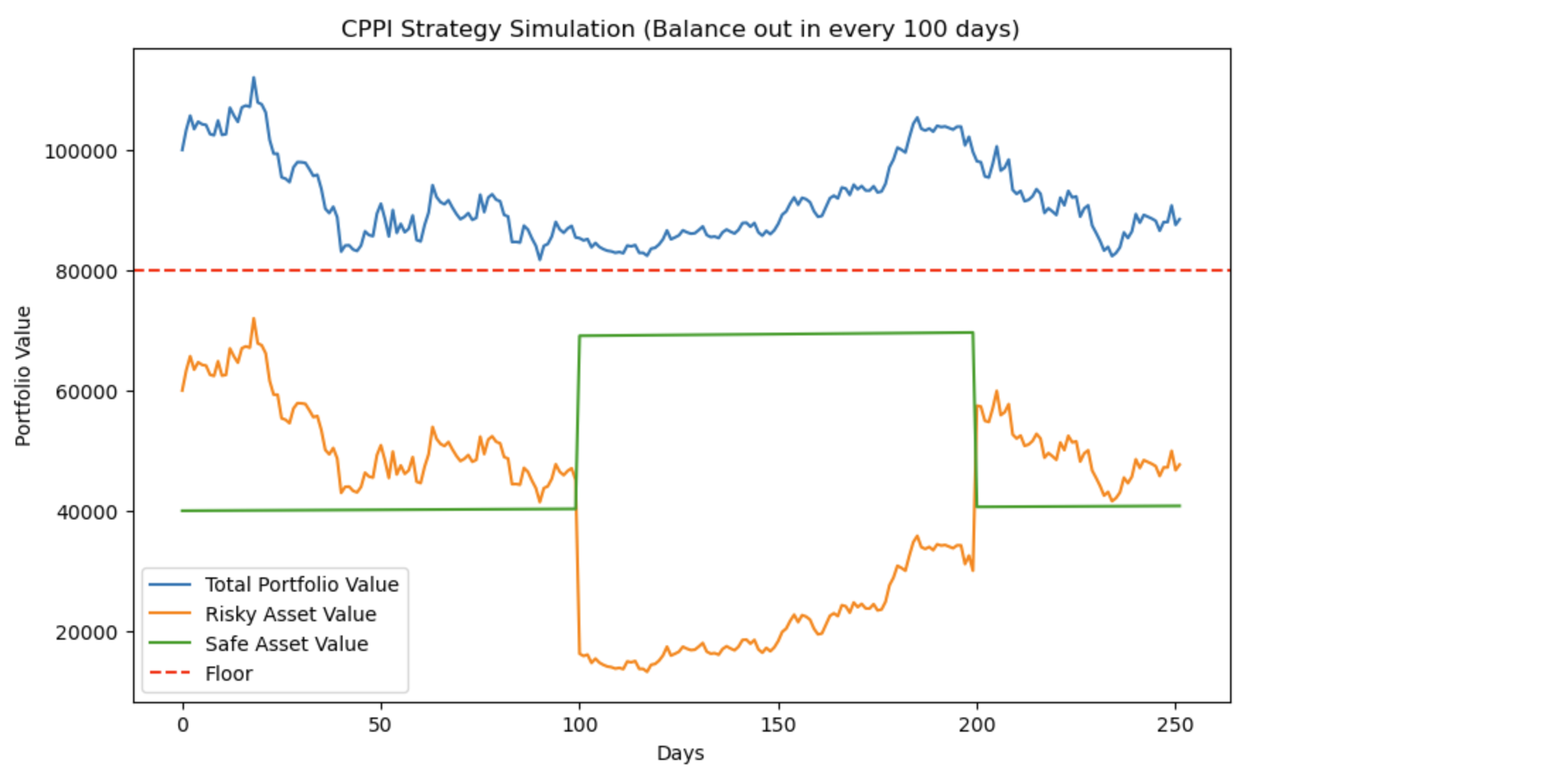
ここまできたらなんとしてもフロアを切らせたくなってきました。リスク資産の予想リターン(30%)、リスク資産のボラティリティ(70%)のリスク資産に投資しましょう。さらに資産のバランを調査する日数を100日に1回にしてみます。

• リスク資産の予想リターン(30%)
• リスク資産のボラティリティ(70%)
• セーフ資産のリスク利率(2%)
• 調整頻度(100日)

この条件でもフロアを下回らずに1年間運用できてますね。。。

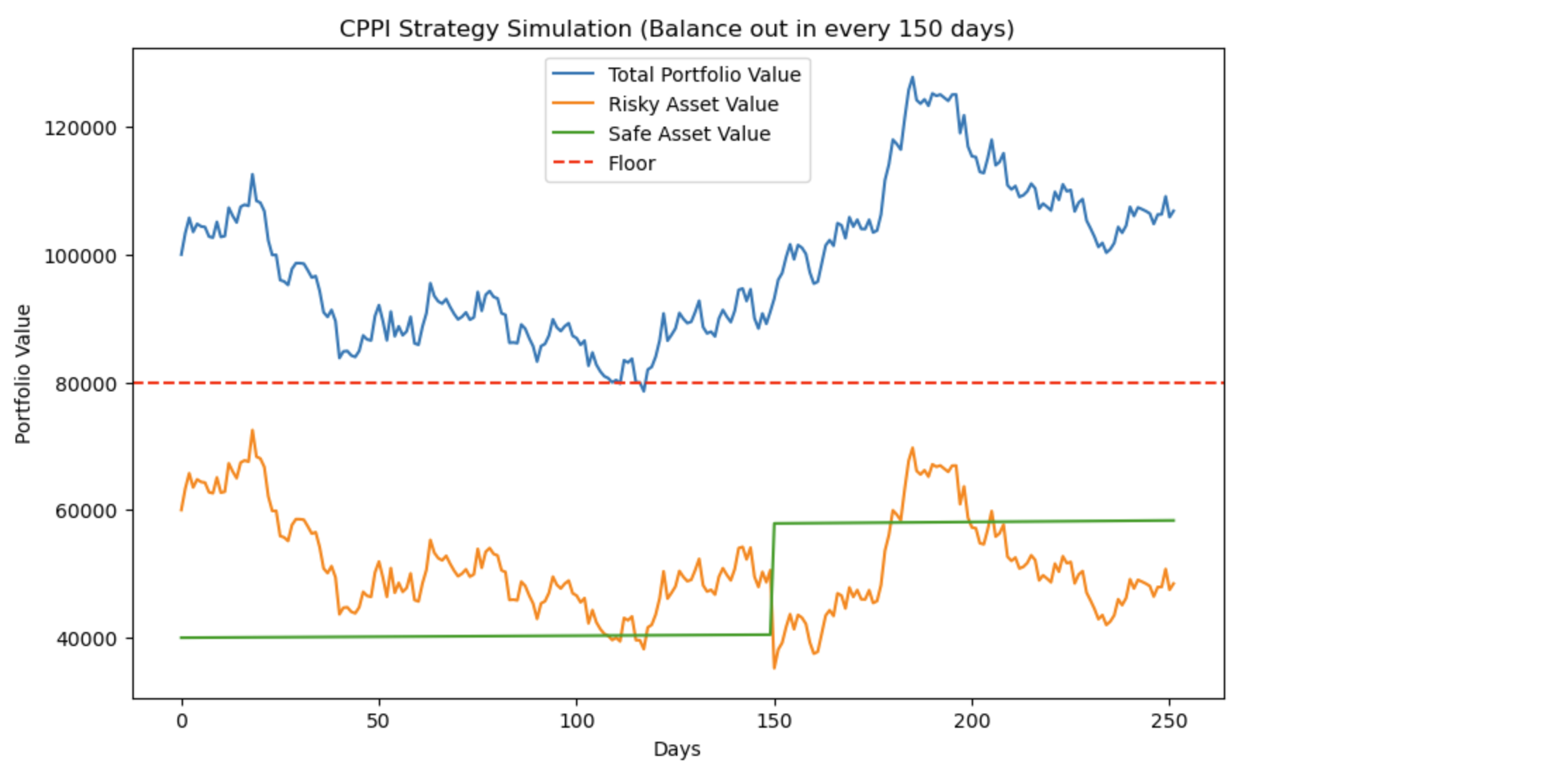
リスク資産の予想リターン(40%)、リスク資産のボラティリティ(70%)のリスク資産に投資しましょう。さらに資産のバランを調査する日数を150日に1回にしてみます。

• リスク資産の予想リターン(40%)
• リスク資産のボラティリティ(70%)
• セーフ資産のリスク利率(2%)
• 調整頻度(150日)

120日目あたりでやっとフロアを下回りました。しかし、150日に資産バランスを調整したのちは順調に成長し、プラスで1年を終えてますね。

終わりに

今回はポートフォリオのダイナミックバランシング戦略の1つであるCPPI（Constant Proportion Portfolio Insurance）についてご紹介しました。CPPI戦略は、資産の最小価値（フロア）を保証しつつ、市場の上昇に伴いリターンを追求する方法でした。一見レバレッジをかけてリスクを取っていそうな雰囲気なのですが、資産の割合をリアルタイムで調整することで、バッチリと資産を運用できることがわかりました。
次回は実際の株式のデータを使ってシュミレーションしてみたいと思います。

おまけ

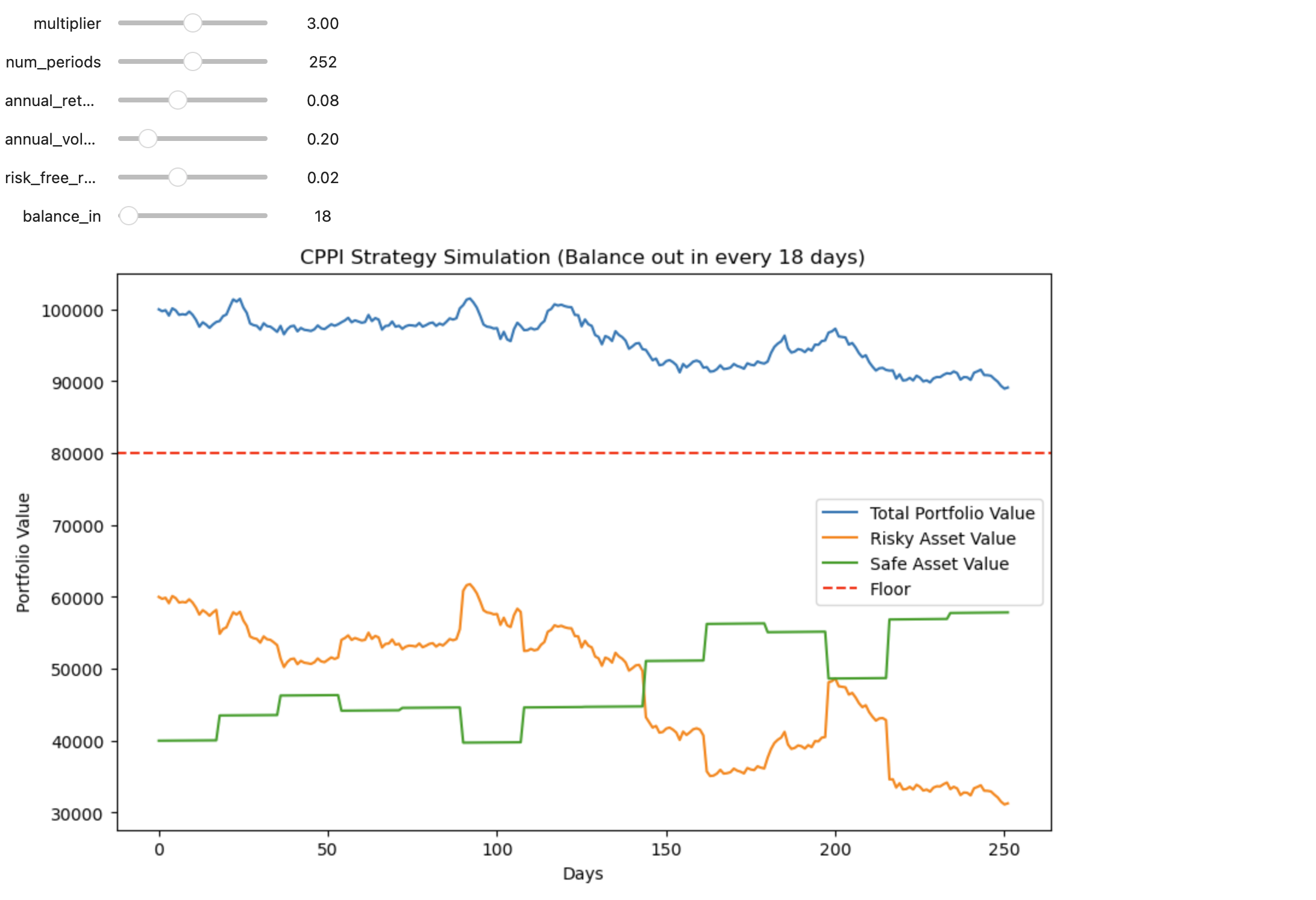
Jupyter Labのipywidgetsを使いインターアクティブなグラフを作りました。Nodejsが必要ですが、是非。