TL;DR
言語モデルBERTを用いたテキスト分類タスクにおいて、事例ベースの解釈性手法TracInを試しました。
はじめに
機械学習やディープラーニング技術が広く普及し、テーブルデータ・画像・テキストなど様々なデータの分析で活用されてきています。
しかし、機械学習の問題の一つに、機械学習モデルの挙動が人間にとって理解しにくいことがあります。
線形回帰モデルなどの解釈しやすいモデルならまだいいのですが、ディープラーニングだとパラメータ数が膨大になりますので挙動の理解は困難になります。
実用上、機械学習モデルの解釈が得られると嬉しいことがあるので、
私が普段扱っている自然言語処理のBERTモデルに対して解釈性を得る手法を試してみます。
試す解釈性手法
機械学習モデルを解釈する方法として、今回は事例ベースのアプローチを試します。1
教師あり学習では、学習データからモデルのパラメータを学習します。
つまり機械学習モデルが行う予測は学習データから影響を受けています。
このことを考えると、「あるテストデータに対する予測結果に対して、どの学習データがどのように影響を与えたのか」を知りたくなります。
これが事例ベースのアプローチの目指すところです。
この記事では事例ベースのアプローチであるTracInを取り上げます。
TracIn概要
TracInはGoogleが2020年に発表した手法です。
論文リンク
| Liu, Frederick, Satyen Kale, and Mukund Sundararajan. "Estimating training data influence by tracing gradient descent." Proceedings of the 34th International Conference on Neural Information Processing Systems. 2020. |
|---|
実装はこちらで公開されています。
以下、簡単に考え方を説明します。
詳細は論文を確認してください。
理想的な考え方
学習するモデルのパラメータ$\boldsymbol{w}$、データの事例を$z$として損失関数を$l(\boldsymbol{w}, z)$とします。
事例$z$だけを学習したとしてパラメータが$\boldsymbol{w}_t \rightarrow \boldsymbol{w}_{t+1}$に変化するとき、事例$z'$についての損失の変化を考えます。
損失の変化:$$l(\boldsymbol{w}_{t}, z') - l(\boldsymbol{w}_{t+1}, z')$$
この変化を事例$z$を学習したことによる事例$z'$の予測への影響と考えましょう。
良い影響がある場合、$z'$に対する損失は小さくなります。例えば、クラス分類では$z'$の正解クラスを予測しやすくなるようにパラメータが変化します。
逆に悪い影響がある場合は損失が大きくなります。クラス分類であれば正解クラスを予測しにくくなるようにパラメータが変化します。
学習の設定によって同じ事例が複数回学習されることがあるため、事例$z$の事例$z'$への影響は和で表現されます。
事例$z$の事例$z'$への影響: $$TracInIdeal(z, z') = \sum_{t:zを学習するt} l(\boldsymbol{w}_{t}, z') - l(\boldsymbol{w}_{t+1}, z') \tag{1}$$
計算を簡単にする
上記の式(1)だと、パラメータの更新前後の$\boldsymbol{w}_t, \boldsymbol{w}_{t+1}$を扱う必要があります。
計算がしにくいので、損失の変化を損失関数の一階微分を使って近似します。
$$l(\boldsymbol{w}_{t+1}, z') \approx l(\boldsymbol{w}_t, z') + \nabla l(\boldsymbol{w}_t, z')(\boldsymbol{w}_{t+1} - \boldsymbol{w}_t)$$
ここでパラメータの更新式は$\eta_t$を学習率として$\boldsymbol{w}_{t+1} - \boldsymbol{w}_t = - \eta_t \nabla l(\boldsymbol{w}_t, z)$であるため、次の式変形ができます。
$$l(\boldsymbol{w}_{t}, z') - l(\boldsymbol{w}_{t+1}, z') \approx \eta_t \nabla l(\boldsymbol{w}_t, z') \nabla l(\boldsymbol{w}_t, z)$$
この近似により、パラメータ更新前後の重みを保持する必要がなくなります。
$\boldsymbol{w}_t$時点での$z$, $z'$に対する損失関数の勾配(と学習率)があれば良いことになりました。
ミニバッチを考える
実際の学習では1事例だけ取り出すのではなく、複数の事例をまとめたミニバッチと呼ばれる単位で計算を行うことが多いです。
1事例だけの影響を考えることは現実的でないので、ミニバッチ内で平均を取るような処理を考えます。
$$TracIn(z, z') = \frac{1}{B}\sum_{t:z \in B_tであるようなt} \eta_t \nabla l(\boldsymbol{w}_t, z') \nabla l(\boldsymbol{w}_t, z) \tag{2}$$
つまりミニバッチに含まれる各事例に対して、平等に損失の変化分を還元します。
さらに計算を簡単にする
上記の式(2)では、学習する途中のパラメータや損失関数の勾配を取り出す必要があります。
実際に学習をシミュレートするか、学習途中のパラメータや勾配が保存されていないと計算できません。
これでは実現困難です。
ところで、機械学習では訓練途中のモデルを保存する慣習があります。
保存された途中のモデルをチェックポイントと言います。
例えば複数epoch学習を行い、1epochごとにチェックポイントを保存するとします。
このときのチェックポイントを利用して、事例$z$に対する勾配を計算することを考えます。
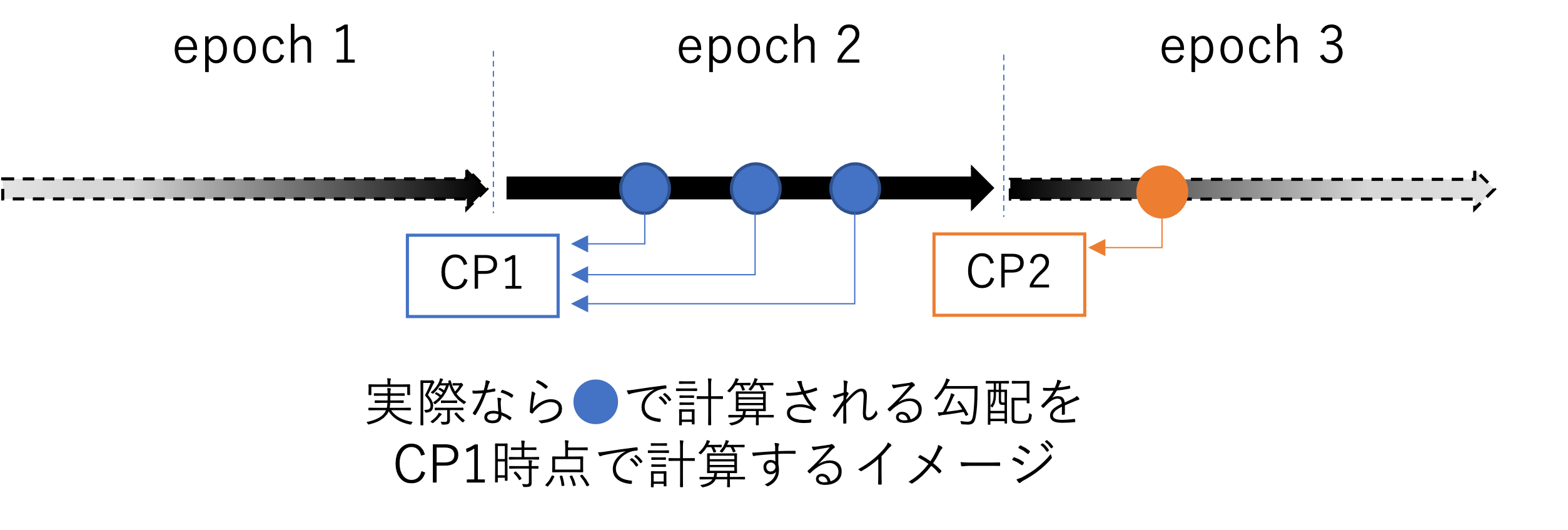
(下図のイメージを確認してください。CPはチェックポイントを指します。)
式(2)では事例$z$が学習されるタイミングでの重みパラメータを用いて計算したいところですが、それだと学習をシミュレーションしなければならず、計算がとても大変です。
既に保存されているチェックポイント時点でのパラメータを代わりに用いることで、学習をシミュレーションする必要がなくなります。
代わりに、本来計算されるはずだった勾配とはずれが生じます。それぞれの事例について、実際の計算タイミングではなくepochの最初に計算されたとみなすイメージです。
$$TracInCP(z, z') = \sum_{t:checkpoint時点} \eta_t \nabla l(\boldsymbol{w}_t, z') \nabla l(\boldsymbol{w}_t, z) \tag{3}$$
これにより、実際の学習過程をシミュレーションする必要なく、チェックポイントのモデルを用いて各事例に対する損失を計算すればよくなりました。
つまりどういう計算をするのか
以上から、次の処理を行えばよいです。
- 通常の学習を行う途中、epochごとにチェックポイントとその時の学習率を保存する。
- 訓練事例$z$、テスト事例$z'$について、それぞれのチェックポイントのモデルを用いて、損失関数の勾配を求めて式(3)を計算する。
実験
ここから、日本語データを用いて行った試行について紹介します。
今回は森羅2022 Wikipedia構造化プロジェクトで公開されているデータを用いて、Wikipedia記事のカテゴリを予測するテキスト分類を行いました。この分類モデルの予測結果に対してTracInを使って分析してみます。
データの詳細はプロジェクトのページをご確認ください。
データセットのうち訓練データとして公開されているデータを分割して、改めて訓練データとテストデータとして扱っています(森羅2022プロジェクトのテストデータは使用していません)。
このデータはWikipediaから2019年1月21日にダンプされているもので、現在のWikipedia記事内容とは異なる可能性があります。
データのサンプリング
カテゴリの偏りが結構あるので、適当に件数を抑えるためサンプリングしました。
具体的には訓練データにおいて、各カテゴリ最大でも200件までのサンプリングを行いました。
モデル・学習について
BERTはNICTの公開しているBERTにしました。使用方法は次をご確認ください。
タスクへのファインチューニングについて、性能追求はあまり重要ではないため、ハイパーパラメータは適当に設定しました。
バッチサイズは16、学習率は3e-5、学習エポック数は5を設定し、他のパラメータはHuggingfaceの学習スクリプトのデフォルトのままです。
実装について
著者のリポジトリにて画像認識タスクに適用するnotebookが公開されています。これを参考に実装しました。
また計算を簡単にするため、次の二点の変更をしています。これらは公式リポジトリのFAQを参考に実施しました。
- BERTはパラメータ数が多いため、クラス分類のための分類レイヤーのみを対象に勾配を計算しました。
- 今回の実験では式(3)において、全てのチェックポイント時点の学習率を1として扱いました。
結果の観察
学習したモデルが推定を誤っている事例に対する分析をします。2
テストデータのうち推定を誤った事例に対して、学習データのうち良い影響(正解する方向の影響)と悪い影響(誤る方向の影響)を与えているサンプルを見てみます。
詳細な結果を載せると大量になるので、わかりやすい例をピックアップしています。
次の例はテストデータのうち誤っている事例です。アクワイアというボードゲームについてのテキストが対象です。正解ラベル「玩具名」であるところ、「ゲーム名_その他」と誤っています。(参考:アクワイア 2019年1月21日直前の記事履歴)
アクワイア ( Acquire ) は 、 アメリカ の ボードゲーム 。 1962 年 に シド ・ サクソン に よって 創案 さ れ 、 かつて あった 3 M の ゲーム 部門 から 発売 さ れて いた が 、 1976 年 に アバロンヒル が 権利 を 買収 した 。 (後略)
良い影響を与えたサンプル
比較的良い影響を与えた訓練サンプルをピックアップします。
これらのサンプルは、アクワイアのテキストを「玩具名」(正解クラス)と予測するように影響しました。
一つ目は『オセロ』についてのテキストです。この訓練サンプルは正解ラベル「玩具名」です。(参考:オセロ_(ボードゲーム) 2019年1月21日直前の記事履歴)
オセロ ( Othello ) は 、 2 人 用 の ボードゲーム 。 交互に 盤面 へ 石 を 打ち 、 相手 の 石 を 挟む と 自分 の 石 の 色 に 変わり 最終 的に 石 の 多い 方 が 勝ち 。(後略)
二つ目はTRPG『ハイパートンネルズ & トロールズ』のテキストです。この訓練サンプルは正解ラベル「玩具名」です。(参考:ハイパートンネルズ & トロールズ 2019年1月21日直前の記事履歴)
『 ハイパートンネルズ & トロールズ 』 と は 、 テーブルトーク RPG の ルール システム の 一 つ 。 プレイヤー は ファンタジー 世界 の 一 人 の 冒険 者 と なり 、 ゲーム マスター から 提示 さ れた 課題 ( ダンジョン 探索 や 誘拐 事件 の 解決 など ) を クリア する こと に なる 。(後略)
悪い影響を与えたサンプル
逆に、アクワイアのテキストの予測に対して、悪い影響を与えた訓練サンプルをピックアップします。
これらのサンプルは、アクワイアのテキストに対して、「玩具名」以外のクラスを予測するように影響しました。
一つ目は『バトルドーム』についてのテキストです。この訓練サンプルは正解ラベル「ゲーム名_その他」です。(参考:バトルドーム 2019年1月21日直前の記事履歴)
バトルドーム ( 英語 : Battle Dome ) は 、 米 Anjar 社 が 版権 を 持つ 玩具 である 。 日本 で は ツクダオリジナル 、 また その 事業 を 引き継いだ パルボックス 、 メガハウス より 発売 さ れて いた 。(後略)
『ハイ・スピード』というピンボールマシンについての記事です。この訓練サンプルは正解ラベル「ゲーム名_その他」です。(参考:ハイ・スピード 2019年1月21日直前の記事履歴)
『 ハイ ・ スピード 』 ( High Speed ) は 、 米 ウィリアムス 社 が 1986 年 に 発売 した ピンボールマシン 。
これらのサンプルから、アクワイアのテキストと似たテイストを感じます。
これらのサンプルを学習した結果、このようなテキストに対して「ゲーム名_その他」を推定する方向にパラメータが調整されているはずです。このため、アクワイアのテキストに対する予測に悪い影響を及ぼしている(「玩具名」ではなく「ゲーム名_その他」方向に調整される)ことは納得できます。
「ゲーム名_その他」カテゴリ
『アクワイア』の「玩具名」ラベルの予測について、訓練データの良い影響と悪い影響を観察しました。
今度は逆に、上記の訓練サンプルが「ゲーム名_その他」カテゴリのテキストに及ぼしている影響を確認してみます。
『目隠し将棋』についてのテキストです。正解ラベルは「ゲーム名_その他」で、モデルは推定に成功しています。(参考:目隠し将棋 2019年1月21日直前の記事履歴)
目隠し 将棋 ( めかくし しょうぎ ) は 、 将棋 の 遊び 方 の 一 つ である 。
このサンプルの予測に対して、『オセロ』『ハイパートンネルズ & トロールズ』は悪い影響(「ゲーム名_その他」以外を予測する方向)を及ぼしていることがわかりました。
また『バトルドーム』『ハイ・スピード』は良い影響(「ゲーム名_その他」を予測する方向)を及ぼしていました。
たまたまかもしれませんが、これらの訓練サンプルはそれぞれ「玩具名」「ゲーム名_その他」ラベルの予測に強く影響していそうですね。
まとめ
言語モデルBERTを用いたテキスト分類タスクにおいて、事例ベースの解釈性手法TracInを試しました。
応用として、平均的にモデルの予測に対して悪影響のあるサンプルを除くような処理(データのクリーニング)も考えられますが、今回は時間の関係で取り組んでいません。
上記で内容で間違いのご指摘やコメント等あればお願いします。