前回の記事（ https://qiita.com/shunga/items/33937906188674b85a7b ）で使ったAppleのサンプルコード"Hello Triangle"のSwift移植に成功したのはいいが、アニメーション要素がないのでなんだか寂しかった。頂点座標の扱い方がわかったことだし、せっかくだからちょっと動かしてやろうと思い立った。
#設計
ひとまず三角形をクルクル回すアニメに挑戦する。Z軸とか立体的なやつは後でいい、とりあえず平面のやつをクルクル回してから応用編に行こう。しかしどうすればいいんだろう。そもそもシェーダーでアニメーションさせるってのはどういうことなんだろうと調べてみたがよくわからない。GL Sandboxの作例がMetalに移植できるらしい（参考：［iOS］ Metalシェーダことはじめ - WebGL/GLSLの豊富なサンプルを参考にMSLを書く https://qiita.com/shu223/items/dd5a53b8c291abe30fc2 ）ので実際にコードを見てみたが、何をやっているのか全く理解できない。仕方がないので自分で考えるしかない。
とにかく描画1フレームごとにちょっとずつ座標をずらせばアニメーションになるだろう。角度を少しずつ変えていけば回転のアニメになるに違いない。ということはたぶん三角関数が必要になるな。三角関数は高校の時に0点をとったことがある。だもんで『別冊ニュートン 三角関数』を買って一から勉強し直した。
##そもそも座標の回転って何だ？
なるほど三角関数の概要は分かった。ようするに座標を直角三角形として見立てたとき、xやyの値は角度θによって決まってくるというわけか。サインコサインとか難しいことを言っているように見えるが単に倍率だ。んで半径...この場合原点(0, 0)までの距離とcosθとかを掛け算すれば(x, y)が自ずと導かれると。んじゃ回転するアニメーションはこの角度θを変えていけばいいわけだ。この場合の三角形で底辺や高さが半径の長さを超えることはないから、sinθもcosθも1（あるいは-1）を超えることはない。わけのわからん数字を入れそうになった時はこれを思い出すことにした。
##角度はラジアン
print(sin(30.0)) // = -0.9880316240928618
というわけでPlaygroundでsin(30)とやってみたが動かない。どうやらFloatとかDoubleじゃないとアカンらしい。そこで30.0と入れたらわけの分からない数字が出てくる。これ0.5になるんじゃないの？
調べるとどうやらこの角度にはラジアンを入れてやらねばならんようだった。ラジアンて三角関数の本にも書いてあったな。確か半径と円周の長さがイコールになる時の扇型の角度を1とするんだっけ。だから360度は2πになる。だもんで30度の場合は1/6にπを掛け算すればいい。当初、それを計算するために「いちいち分数を実数にするのめんどくせーな」とか思ってたけど、"1/6"と式に書いてしまえばそれで済む話だった。πの値はFloat.piとかDouble.piとか書くとSwiftが精度に応じた定数をくれる。
print(sin(1/6 * Float.pi)) // = 0.5
よしよし。というわけで180°は π = 3.1415925ラジアン(Float)ということになってくる。これも数字の感覚として覚えておくことにした。
ラジアンというのは面積とか円周の話をする時に都合がいいという話である。確かに、円周上を移動する点の移動距離を角度と同じ数字で扱えるわな。
#実装
var radianCount:Float = 0
func incrementRadian() {
radianCount += 0.01
if radianCount >= 2 * Float.pi { //2πに達したら0に戻す
radianCount = 0
}
}
というわけでラジアンを少しずつ増やしていくプロパティをレンダラーに作った。毎フレームの描画の最後にこのメソッドを使えば、毎回0.01ずつ増やせる。ラジアン値がどれだけ増えようと三角関数は正しく動いてくれるけど、なんかずっと増やしっぱなしというのは無駄遣いのような気がしたので一周分回ったら0に戻すようにした。
renderEncoder!.setVertexBytes( &radianCount,
length: MemoryLayout<Float>.size,
index: 2 )
でもって今度はそのラジアン値をシェーダーに持っていくメソッドを追加する。これは前回、_viewportSizeを送ったのとほぼ同じことをやっている。setVertexBytesはUnsafeRawPointerしか受け取ってくれないので、&をつけた変数、つまりアドレス渡しになる。ポインタ廃止とはなんだったのか。
ここでindexを"2"に指定すると、シェーダー側でラジアン値を[[ buffer(2) ]]として受け取ってくれる。この[[ buffer(ナントカ) ]]がSwiftとMSLの橋渡し役のようである。
vertex RasterizerData
vertexShader(uint vertexID [[vertex_id]],
constant AAPLVertex *vertices [[buffer(AAPLVertexInputIndexVertices)]],
constant vector_uint2 *viewportSizePointer [[buffer(AAPLVertexInputIndexViewportSize)]],
constant float *radianCount [[ buffer(2) ]]) //←今回追加したラジアン
{
"AAPLVertexInputIndexVertices"と"AAPLVertexInputIndexViewportSize"は共有ヘッダで定義されたenumであり、単に整数値の0と1だから、それぞれ[[ buffer(0) ]]と[[ buffer(1) ]]と書いてあるのと同じである。今回そこに新たに[[ buffer(2) ]]を追加した。
float newX = vertices[vertexID].position.x * cos(*radianCount));
float newY = vertices[vertexID].position.y * sin(*radianCount));
んでもってレンダラーから貰ったラジアンと座標を掛け算すれば毎フレームごとに動く座標ができるという寸法よ！
#できたーーーーーーー？？？
なぜか予想外に愉快な動きになって爆笑した。 ナンデ？ 使う関数を間違えたのか？ んじゃ今度はtan()にしてみよう....
なんなのその動き。誰に教わったの。俺か。クソッ、どうしてこんなことに....
##そもそも「図形が回転する」ってどういうことだ？
これはこれで面白いがどうにも不可解だ。そもそも「図形を回転させる」とはどういう操作なんだ？テーブルの上で折り紙を回したりしていろいろ考えた。
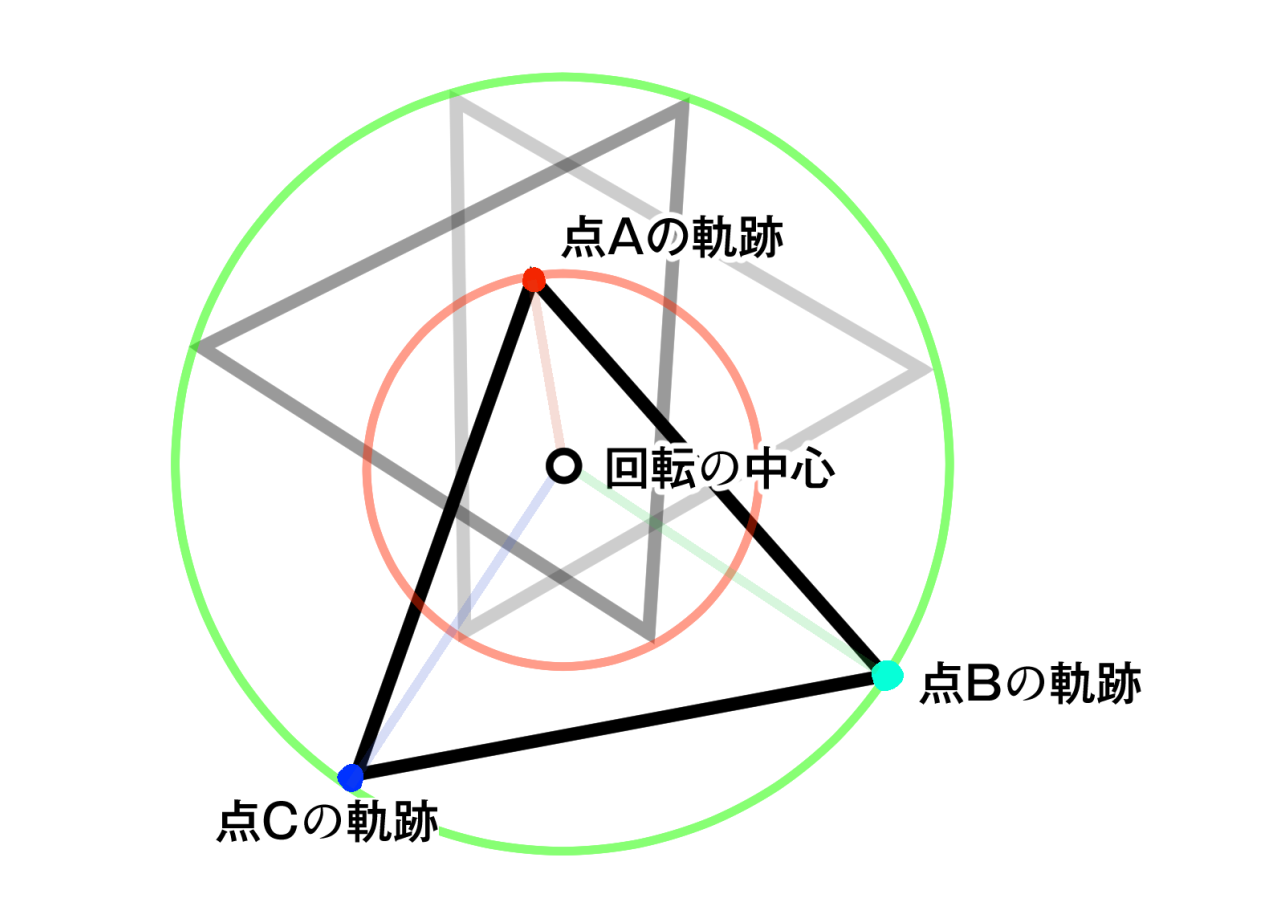
つまり、各頂点は図形の回転軸と頂点とを結ぶ線を半径とした円軌道を描いている。そうか、上では単に座標値にサインコサインしただけで半径とかそういう操作を全くしていなかった。そもそもsinθもcosθも半径との対比じゃないか。
##座標から現在の半径とラジアンを算出する
半径は回転の中心（今回は原点0,0）との距離だから、単純に三平方の定理でx^2 + y^2 の平方根を出せばいい。しかし、ラジアンはどうすればいいんだろう？ 今回は別に回転のスタート地点を指定しているわけではないから、最初のラジアンにどんな値を入れても回ってさえいれば問題ないわけだが、そういうのは将来的に困る。
半径と角度から座標を出す関数の逆のことをするんだよなぁ....？と考えながら『別冊ニュートン 三角関数』を開くと、ちょうど逆三角関数のことが載っていた。アークコサイン！やっぱこういうのがあるんじゃんね。
##改修
float newX = vertices[vertexID].position.x;
float newY = vertices[vertexID].position.y;
float r = sqrt(newX * newX + newY * newY);
float radian;
if (newX < 0 && newY < 0) {
radian = acos(newX / r) * -1;
} else {
radian = atan(newY / newX);
}
newX = r * cos(radian + *radianCount);
newY = r * sin(radian + *radianCount);
というわけで、貰った座標から半径rと現在のラジアンを求めて、そこから毎フレーム増えた分のラジアンを加味して座標を得るよう改修した。座標の値からアークタンジェントを使ってラジアンを求めている。座標の値がマイナス同士だと割り算した時に正負がおかしなことになるので、その時だけアークコサインを使うようにした(acosも(-x,y)と(-x,-y)を区別できないが、出てきたラジアンをマイナスすれば(-x,-y)の時の角度が得られる)。計算途中で÷0が出てくるからタンジェント関係はあまり使いたくなかったんだけど、そのような心配をよそに期待通りの動きをしてくれた。内部的にどうなってるんだろう？
レンダラーから来る座標は毎回同じなのにその都度半径を求めてるのはなんかバカっぽいが、こうすれば毎回違う値が来るようになっても対応できるし、rに新たに三角関数を使えば拡大縮小みたいな効果が得られる。
##後日談
そういえばatan()にπを足せば(-x, -y)の時も普通に機能するんじゃないか？ということをtwitterに書いたらatan2()関数の存在を教えて貰った。これならプラスとかマイナスとか気にする必要なくめちゃくちゃ簡単に書ける。
float radian = atan2(newX, newY); //atan2()は(x, y)の符号に関係なく使える
#できたーーーーーー！
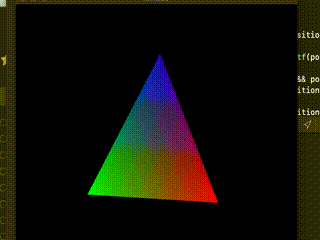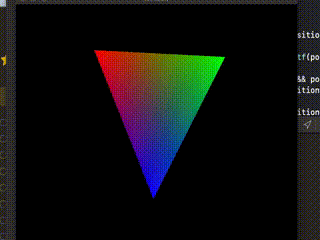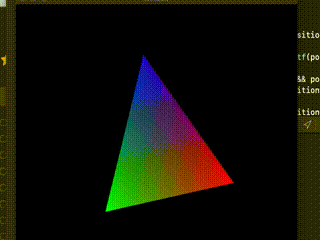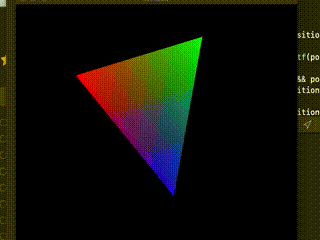
というわけでこれでやっと思い通りの結果になった。一番手間のかかったやつが一番地味になってしまったが、とても勉強になったので良しとしよう。次はマウスでドラッグしたりとかペンタブレットの筆圧に応じて大きさが変わったりというようなことにも挑戦したいが、今回はここまで。
##学んだこと
- 三角関数を使うと周期的な値がいい感じに得られる
- タンジェントを使うと派手な効果になる
- 数学が0点でも勉強すればダイジョブ