AtCoder Heuristic Contest 003に参加し、2,855,269,030,186 点で1000人中107位でした。
(暫定テスト時、95,228,989,577で103位)
ヒューリスティックコンテストはいろいろな解法があるのが面白いところだと思うので、備忘録も兼ねて自分がやった内容と点数の推移をまとめてみようと思います。

問題設定

厳密な問題定義はhttps://atcoder.jp/contests/ahc003 を見てもらえればと思いますが、
ざっくりいうと、下記のようなインタラクティブな問題設定です。

30×30の頂点を持つ辺の長さが不明なグリッドグラフが与えられる。
1000回下記のクエリへの回答を行う
- クエリ：始点$s(s_{i}$,$s_{j})$と終点$t(t_{i}$,$t_{j})$
- 回答：$s→t$のルートを示す文字列(例えば右に２回、下に３回進むなら"RRUUU")
評価は下記の計算式によって計算されるため、なるべく短くなるような経路を回答していきたい。特にクエリ後半になるほど、誤差を小さくしたほうがスコアが良くなる。
辺の重みは完全ランダムによって決定されるわけでなく、行や列ごとに平均や分散が定まっている (厳密には辺の重みの設定方法は2パターンあり、値の範囲などが問題文中に明記されている)

最終得点の計算式
$k$番目のクエリに対する最短路長$a_{k}$、出力されたルートの長さを$b_{k}$として、

round(2312311 \times \sum_{k=1}^{1000} 0.998^{1000-k}\frac{a_{i}}{b_{i}})

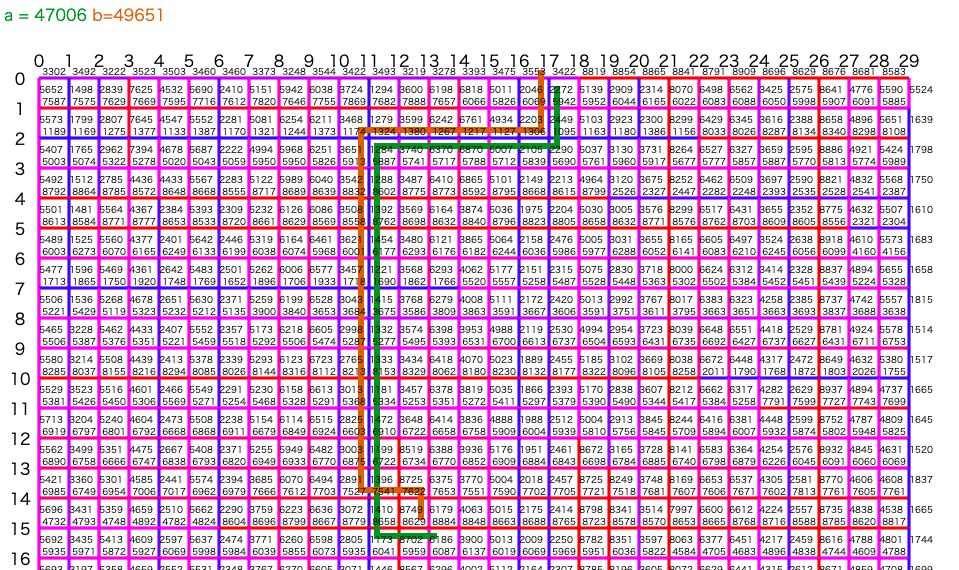
ルートのイメージ

(緑が実際の最短経路で、オレンジが推測した最短経路)

解法要約

最終的な解法(暫定テスト95,228,989,577点)を先に書きます。

以下をクエリ回数(1000回)分繰り返す
1. システムから$s_{k}$,$t_{k}$の座標情報を受け取る
2. $s_{k}→t_{k}$へのルートを探索する
  1. 80回目のクエリまでは、最大1回までしか曲がらず、なるべくグリッドグラフの外側に近いルート
  2. 80回目以降は推定した辺重みを用いてダイクストラ法
3. 探索したルートを出力する
4. システムから提示したルートの長さを受け取る
5. 辺の重みを下記の更新式で更新する
6. 100回目のクエリ以降、10回に1回の頻度で過去のルート全てを用いて辺重みを更新する
7. 50回目のクエリ以降、50回に1回の頻度で未通過の辺の重みを行・列ごとに通過済みの重みの平均値で推定し置き換える

辺の重みの更新式

e_{i} ← e_{i} + \alpha \times \frac{(W - \sum_{i \in A} e_{i})}{|A|}

$e_{i}$は現在の辺の推定重み、$A$がルートとして出力した辺の集合、$W$がルートを示したときにシステムから帰ってきたルートの長さ(真の値)、$\alpha$が辺重みの更新を急にしすぎないようにするためのパラメータで、今回は0.1で設定しました。
前半はなるべく、いろいろなルートを通るようにして、後半はダイクストラ法で現在の辺重みでの最短経路を取るようにしています。

取組内容とスコア推移

考えたこととスコアが改善した内容を順番に書いていきます。

はじめにやったこと(〜631億点)

最低限必要な関数の作成
- $s, t$の座標を受け取る
- ルートを文字列として返す
- 提示したルートの長さを受け取る
$t_{i}-s_{i}$ だけ下(負なら上)に進む、$t_{j}-s_{j}$だけ右(負なら左)に進むようなルートの作成

一番直感的な方法かと思います。同じようなスコアが並んでいたので、まずはベースラインとして提出する人が多かったようです。

ダイクストラ法の導入(〜877億点)

考えたこと
- なんとなく多腕バンディット問題のような問題設定
- 探索と活用のバランスを考えて$\epsilon - greedy$法のようなことをやるとよさそう
- 前半はなるべくいろんなルートを通って情報収集したい
- 後半は最短経路問題を解けばよさそう
やったこと
- 前半のルートは上下左右に動く回数を決めたあと、動く順番をシャッフル
- 後半はダイクストラを使って最短経路問題を解く
- 辺の重みはそのルートの長さを辺の数で割った重みを配分して平均をとる

最後の辺の重みの更新は例えば、辺1-辺2-辺3を通るときにシステムから返ってきた長さが60だったとき、3つの辺にそれぞれ20ずつコストを配分するようなイメージです。これを繰り返していき、例えば、あるステップにおいて辺1の重みがこれまで4回使われていて${20, 50, 10, 15}$の重みが配分されていたときは、辺1の重みを$\frac{20+50+10+15}{4} = 23.75$のように推定して使っています。

改善①(〜924億点)

ここからは細かな改善の組み合わせなので、導入したらスコアが改善した内容をまとめて書きます。

考えたこと
- 前半のルートはランダムではなく、なるべく使われたことのない辺を通るようにしたい
- 辺の重みの初期値を1からスタートすると1回通っただけで辺の重みが急激に上昇してしまう
- 辺の重みを均等に配分するのはあまり良くない気がする
やったこと
- これまでに通った辺の回数を記録しておき、前半は通過回数の少ない辺がある方向へ進む
- 辺の初期重みを2000で設定する(いくつか値を設定してスコアから調整)
- 辺の更新式を下記のように比率から推定する方法に変更

e_{i} ← e_{i} \times  \frac{W}{ \sum_{i \in A}e_{i}}

初期値だったり、辺の重みをどのくらい大きく書き換えるかの設定で、スコアが大きく変化することが実験している中でわかりました。

改善②(〜944億点)

考えたこと
- 辺の重みの更新を１度しか使わないのはもったない。過去のルートの重みの差分を繰り返し利用できないか？
- 改善①で入れた辺の重みの更新方法は、序盤で重みが増えた辺ほど優先的に重みが増えてしまうのではないか？
- 問題設定をよく読んでみたら、各辺の重みは一様ランダムではなく、行・列ごとに平均や分散が決められている。また、同じ行・列であっても途中で平均が切り替わる生成パターンもある。
やったこと
- 定期的にこれまで通ったルートの情報を見直し、それらを使って辺情報を更新する
- 辺の重みを下記の更新方法へ変更し、急激な辺重みの変化を抑えるためにパラメータ$\alpha$を追加
- ある程度辺の情報が溜まってきた段階で、未通過の辺の重みも推定して更新する

辺の重みの更新式

e_{i} ← e_{i} + \alpha \times \frac{(W - \sum_{i \in A} e_{i})}{|A|}

強化学習のQ学習とかだと学習率をかけて更新しているのを思い出し、似たようなことをしてみました。また、学習率$\alpha$を使うと1回の更新であまり辺の重みが更新されないので、これも強化学習における経験再生のように過去の経験(ルート)を保存しておいて定期的に更新に利用するようにしました。

また、辺が実は完全ランダムではなく行・列ごとに法則を持って生成されていることを利用し、例えば$i$列目にある20本の辺が既に通過済みであるならば、残り10本の辺重みは未通過であっても、通過済みの辺重みの平均に置き換えるような処理をしました。
(ちなみに、実はここまで来て辺が完全ランダムでないことに初めて気づきました...最初に問題文はしっかり確認したほうがいいですね)

改善③(〜952億点)

考えたこと
- スコアの悪いデータを可視化してみると、辺の重みが行・列の途中で切り替わるような生成方法のデータのときが多い
- グリッドの内側と外側の辺で通過回数が大きく異なり、外側の辺は探索が不十分な可能性がある
- 辺の重みが最低値に設定した1000に張り付いている辺が多い
やったこと
- 前半の探索方法をなるべく外側の辺をたくさん通るように変更
- 辺の最低重みを100まで減らす
- 辺の初期値、探索→活用を切り替えるタイミング、辺の重みを更新する学習率のパラメタ調整

改善②までやってアイディアが枯渇したので、可視化を通じてスコアの悪い場合を眺めました。すると、グリッドの外側を通る場合にルートを大外ししてることに気づいたので、なるべく前半でそのあたりを通るようにしたいと思い、ルートの選択時になるべく外側に近い方へと進むアルゴリズムに修正したところ、スコアが950億点を超えました。
最後にパラメタ調整ですが、optunaなどを使って自動化することも考えたのですが、手で動かした感じ、現在のベストより1億点以上の改善は期待できなかったので、パラメタ調整よりも他のアイディアがないかを優先し、最後に影響の大きそうなパラメータだけ手で調整しました。

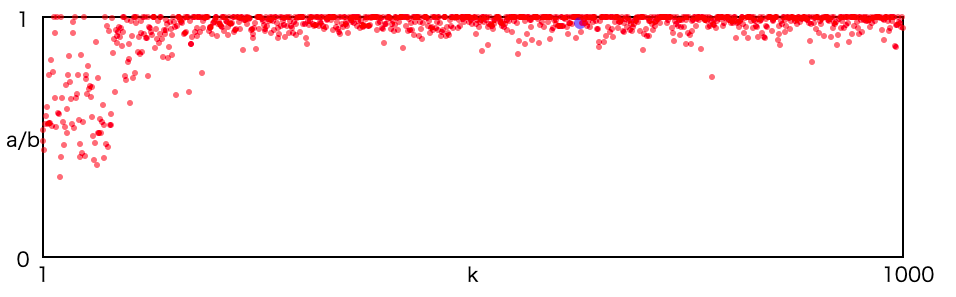
各ステップごとの実際の最短経路と推定した最短経路の比

試したけど上手くいかなかったこと

試したけれども上手くいかなかったことを書きます。
(実装や採用方法が悪い可能性があるので本当に効果が薄いのかは不明です)

$\epsilon-greedy$探索。後半も低確率で未通過の辺を優先する方針を入れてみましたが、スコアが下がりました。スコアの計算方法を見ると、$0.998^{1000}$が0.135くらいになるので探索処理はなるべく前半に全て済ませた方が良さそうです。
辺の通過回数を重みに見立てたダイクストラ法。未通過の辺をなるべく通る意図なら、多少遠回りしてもいいのではないかと思い、通過回数の少ない辺をたくさん通るダイクストラ法を実装しました。結果は悪くないものの最終的に選択したシンプルな外側を探索するルートの方がいい結果になりました。
上記と同様の発想で、あえてグリッドの4隅付近に中継点を発生させて強制的にそこを通るようにもしてみました。これもスコアは残念ながら上がりませんでした。辺の数が多くなる分、推定のぶれが大きくなるのかもしれません。
行・列の途中で辺の重みが大きく変わるケースへの対応。辺の重みが途中で大きく変わるケースを外していることはわかっていたので、「同じ行・列内での辺の重みの分散が大きい = 途中で辺重みが大きく変わっている」と予測し、なるべく平均の差が大きくなるような分割点を求めました。しかし、辺の情報が得られている部分がそんなに多くないためか、この単純な方法では改善しませんでした。

上位者の解法と比べての反省点

AHC003終了後、Twitterやブログなどで共有されていた解法を見て、もっとこうしておけばよかったと思う部分を書きます。

辺重みを回帰問題として、線形回帰などで解く
- グリッドグラフの辺の数が1740本なので1000回のクエリで辺重みを推定するのは大変そうですが、行・列ごとに平均がだいたい決まっているので、それを変数にして60本にすれば、行列ごとの辺の重みはだいたい推定できるようです。
M=1(辺の重みが同じ行・列でほぼ一定),M=2(辺の重みが同じ行・列の途中で変化する)の推定
- 統計的にちゃんと考えるとかなり高い精度で推定できるみたいです。
途中結果の可視化
- 今回はインタラクティブ問題ということもあり、自分のアルゴリズムでの辺の重みなどはprintデバッグでしか見れていませんでしたが、ちゃんと自作で可視化したり、結果をPythonで統計的に見ることが改善につながるみたいです。
ベイズ最適化などを利用したパラメタチューニング
- optunaなどでパラメタチューニングをしている人もいたみたいです。AHC001のときにもパラメタチューニングは考えましたが、実際コンテスト中は他のことを試したくなって手をつけなくなってしまうので、仕組みだけでも事前に作った方がいいのかもしれないです。

まとめ

AHC001,AHC002に続いて3回目の参加でしたが、全体の進め方の流れなどは慣れてきて、計画的に楽しく取り組むことができました。全体の方針は悪くなかった気がしますが、しきい値や更新方法をなんとなく勘で決めてしまうことが多いので、今後は統計的な根拠を持って方針を吟味していけるようにしたいです。
あと、最終提出のファイルを間違えたものを提出してしまい、システムテストで5番くらい順位が下がったので、次回は注意したいです。

備考

暫定テスト952億のときのコードのリンクを張っておきます。
https://atcoder.jp/contests/ahc003/submissions/23098409

AtCoder Heuristic Contest 003 参加記