MATLABで信号処理のアニメーションを作った

はじめに

本記事は、レーダ周りを勉強している人がチャープ信号を使ったパルス圧縮について理解を深めるために書きました。数式や数学的な厳密性は置いておいて（私もあやしいし・・・）、アニメーションで中身を説明することで、イメージで理解できるようにしてみました。パルス圧縮というとなじみがない人が多いですが、要素としてはフーリエ変換そして、相互相関（マッチドフィルタ）の理解を深めるのにも役立つかと思います。
と高尚なことを書きましたが、私の目的としては、単に、同僚が動くコンテンツを作っているのを見て、私も何かアニメーションを使ったコンテンツを公開したいなと思っただけです。というかいつもマニアックな話題なので、もうちょっと間口を広げたコンテンツ＋アニメーションでいろんな人に見てもらいたいというのが本音です。

環境

• MATLAB2020a
• Phased Array System Toolbox（チャープの生成で使っています）

パルス圧縮とは

パルス圧縮とはレーダ分野で使われている方法で、線形に周波数を変調した信号（以下チャープ信号）を送受信し、受信信号にマッチドフィルタを適用することで、パルスを得る技術です。ちょっと専門外の人には聞きなれない単語ばかりで頭に入ってきませんね。一つずつひも解いていきます。

チャープ信号

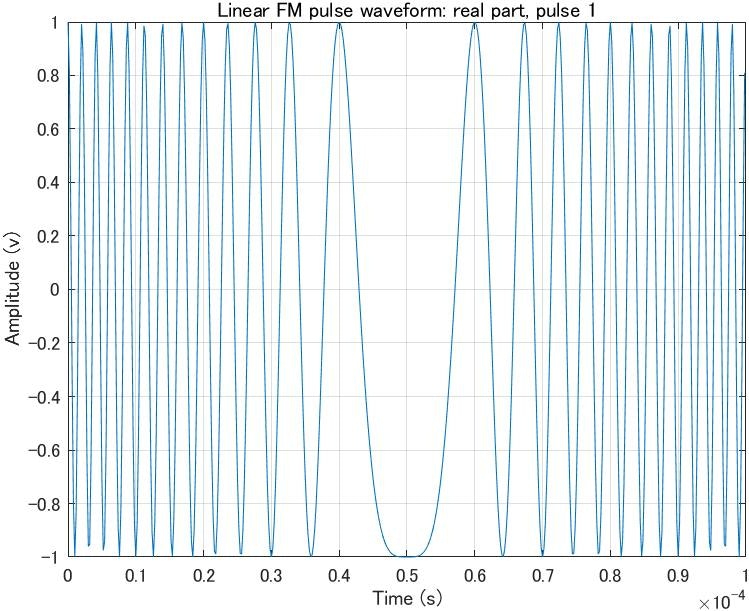
というのはこういう感じの信号です。ちなみに今日は数式は一切使わないで行きます。ソースコードはメイントピックではないので、折りたたみます。随時ご覧ください。

チャープ生成コード

pw = 100e-6;
bw = 1e6;
fs = 5e6;
prf = 1/200e-6;
chirp = phased.LinearFMWaveform("PulseWidth", pw, "SweepBandwidth", bw, ...
    "SweepInterval", "symmetric", ...
    "SampleRate", fs, "PRF", prf);
plot(chirp)

見てわかるように、時間によって周波数が徐々に変化していっています。高周波から始まったのが、徐々に低周波（変化がゆっくり）になり、また高周波に戻っています。このチャープは負から正の周波数に線形で変化させた結果になっています。負から正に変化する過程で絶対ゼロ周波数になりますね。それが0.5sに来ています。負の周波数というとなんか未知の世界のように聞こえるかもしれませんが、単に波の進行方向が逆、という理解で大丈夫です。なので、この信号は左右対称になっています。別に負から正にいかなくても任意の周波数から別の周波数へ時間に対して線形で周波数が変化していればチャープです。もしかしたら線形じゃなくてもチャープっていうのかな、ちょっとわかりませんが、とりあえずこの記事では線形な周波数変調信号をチャープと呼びます。

マッチドフィルタ

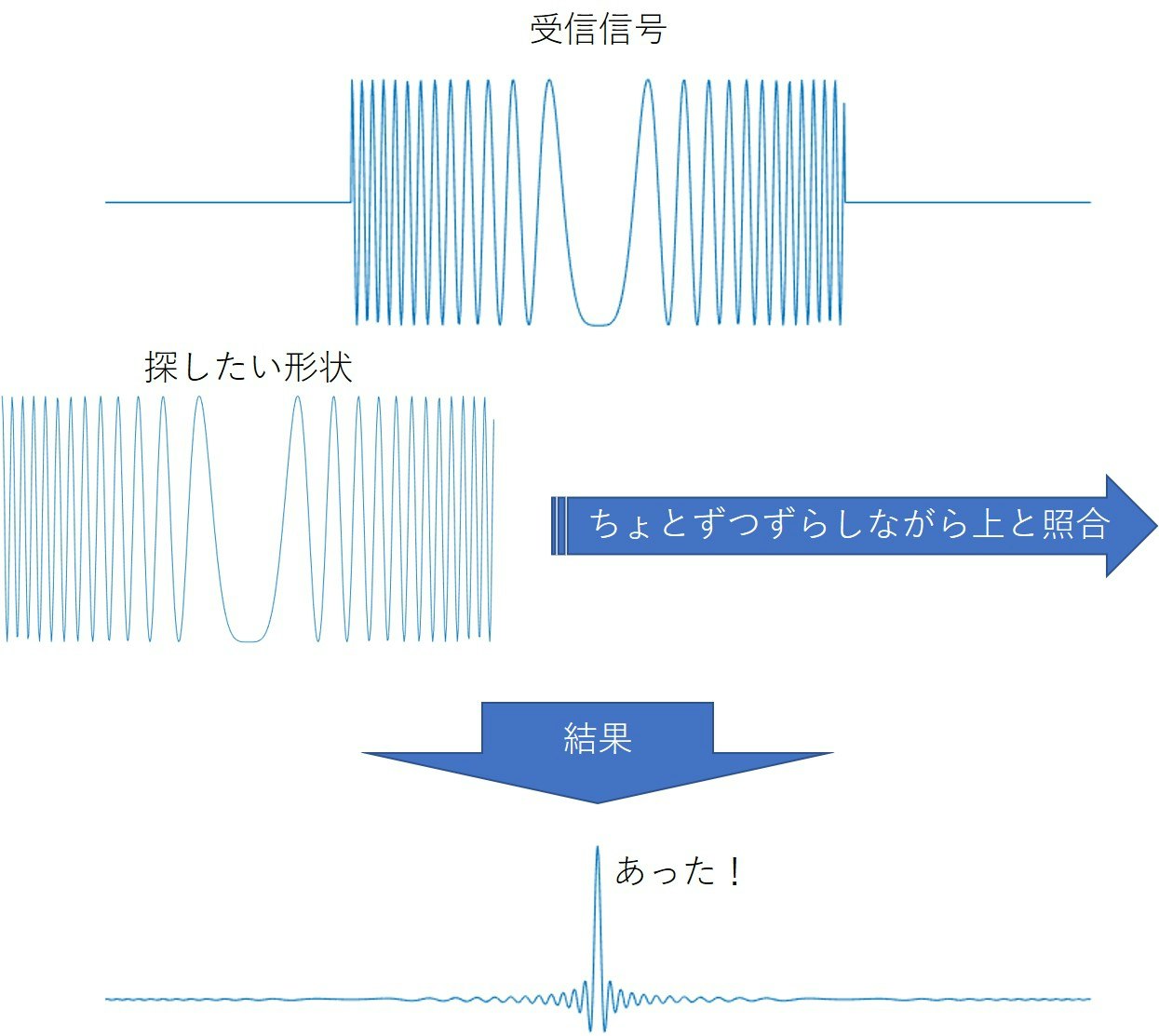
詳しくは後述しますので、ここで概念だけ。要は受信信号の中から送信信号と同じ形状の部分を見つけたら、あった！ってやるだけです。ジグソーパズルのピースを持っていろんなところにはめ込んでみてぴったりはまったところで「ここや！」ってやるのと同じです。
グラフで概念を表してみます。よく見る図ですね

うん、想像できない？ここでアニメーションの登場です。

マッチドフィルタコード

x = chirp() + 0.5*complex(randn(fs/prf,1), randn(fs/prf,1));
x = circshift(x, fs*pw/2); % 真ん中に中心を持ってくる
t = [0:fs/prf-1]/fs;
pulse = chirp();
pulse = pulse(1:fs*pw); % 参照信号（チャープ部分のみ）
pulseSig = [zeros(fs/prf-fs*pw/2-1,1);pulse;zeros(fs/prf-fs*pw/2,1)]; % この信号に対して窓をスライディングさせて受信信号と積を取っていく。
crossCol = zeros(fs/prf,1);

% 表示のfigure生成
fig = figure;
% 三番目のサブプロットにマッチドフィルタの結果をアニメーションで表示
ax3 = subplot(3,1,3);
axis(ax3, [0 1/prf -200 500]);
crossColLine = animatedline;

filename = 'matchedFilter_time.gif';
for i = 1:fs/prf
    pulseSig_i = pulseSig(end-fs/prf-i+2:end-i+1);
    cross = pulseSig_i .* conj(x);
    crossCol(i) = sum(cross);

    % 受信信号と参照信号
    subplot(3,1,1);
    plot(t, real(x),'b');hold on;
    plot(t, real(pulseSig_i),'Color',[0.9 0 0 0.5]);hold off;legend('受信信号','参照信号')
    % 積
    subplot(3,1,2);
    plot(t, real(cross),'Color', 'k', 'LineWidth',0.1);
    hold on;
    posArea = real(cross) > 0;
    area(t, real(cross).*posArea, 'FaceColor','b','FaceAlpha', 0.5);
    area(t, real(cross).*~posArea, 'FaceColor','r','FaceAlpha', 0.5);
    axis([0 1/prf -1 1]);
    hold off;
    % マッチドフィルタ
    addpoints(crossColLine, (i-1)/fs, real(crossCol(i)));

    subplot(3,1,1);title('受信信号と参照信号');
    subplot(3,1,2);title('積')
    subplot(3,1,3);title('マッチドフィルタ');
    drawnow;

    if mod(i,10) == 1 % 10ステップごとにGIFに書き出す
        [A, map] = rgb2ind(frame2im(getframe(fig)),256);
        if i == 1
            imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.1);
        else
            imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.1);
        end
    end
end

マッチドフィルタの効果を示すため、ノイズも乗せてみました。
一番上の図で参照信号と言っているのは送信した信号のことで、ジグソーパズルのピースです。
真ん中の図は、受信信号と参照信号（の複素共役）の積です。複素共役と言ってることからわかるように、実はこれらの信号は複素数で、表示しているのは実部になります。
一番下の図は瞬間瞬間の真ん中の図の積分になります。青い部分の面積の和-赤い部分の面積の和です。
ジグソーパズルがずれたところにあるとき、積を見るとわかる通り0を中心に+成分と-成分が繰り返されており、積分を取ってもキャンセルし合って値は大きくはなりません。
しかし、ピースがぴったりはまったとき、+成分だけになる（位相がキャンセルしてゼロ度になる）ので、積分を取ると値が大きくなります。チャープ信号の場合はぴったりはまらないとなんだかんだ積分がキャンセルしてしまうので、ご覧のように幅の狭い鋭いピークが立つのです。

どうでしょうか。だいぶマッチドフィルタのイメージはつかめたのではないでしょうか。しかしまた別の疑問が出てきます。
なぜチャープ信号なの？他の波形でもいいんじゃないの？
次にそのあたりを見ていきます。

チャープ信号の特性

そもそも短いパルスの周波数特性は？

パルスは幅が狭いほど、広帯域です。この点についてもアニメーションで見ていきましょう。帯域をどんどん太らせていき、結果生じるピークの幅を見ていきます。

スペクトルを太らせていくコード

clear, close all, clc;

df = 1;
freq = [-1000:df:999];
time = [0:1999]/2000;
fsig = exp(j*-2*pi*freq*0.5);

fig = figure;
filename = 'spectrumGrow.gif';
for bw_side = 1:100;
    h_window = zeros(1, numel(fsig));
    h_window(1001-bw_side:1001+bw_side) = ones(1,bw_side*2 + 1);
    fsig_temp = h_window .* fsig;
    subplot(3,1,1); 
    plot(freq, abs(fsig_temp), 'k')
    title('spectrum');

    subplot(3,1,2); 
    cmap = jet(bw_side);
    for i = 1:bw_side
        mask = zeros(1,numel(fsig));
        mask([1001-i,1001+i]) = 1;
        fsig_temp2 = fsig_temp .* mask;
        tsig_temp = ifft(ifftshift(fsig_temp2));
        plot(time, real(tsig_temp), 'Color', [cmap(i,:), 0.2]);
        hold on;
    end
    axis([0 1 -0.001 0.001])
    title('waves of each frequency')
    hold off;

    subplot(3,1,3); 
    tsig = ifft(ifftshift(fsig_temp));
    plot(time, real(tsig), 'k');
    axis([0 1 -0.03 0.1])
    title('generated pulse')

    drawnow;
    if mod(bw_side,1) == 0 %
        [A, map] = rgb2ind(frame2im(getframe(fig)),256);
        if bw_side == 1
            imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.1);
        else
            imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.1);
        end
    end
end

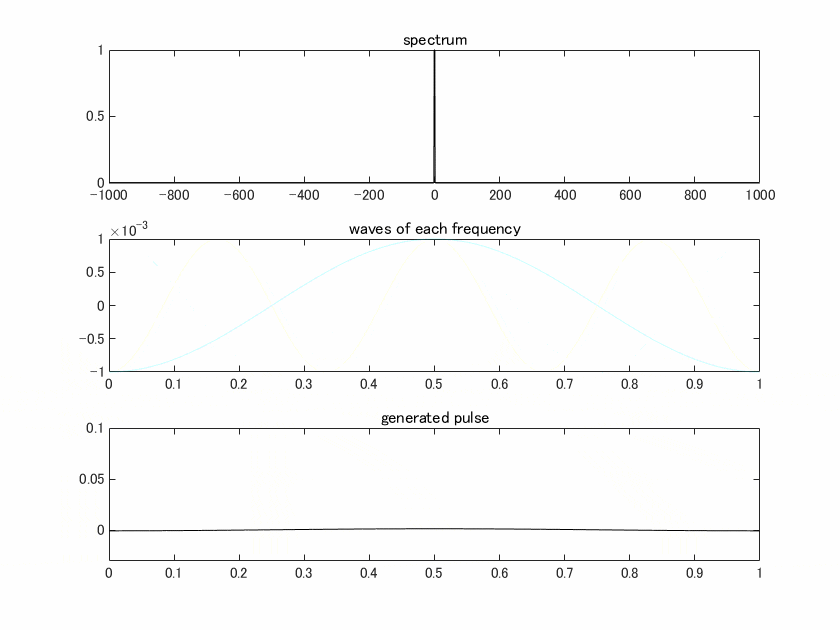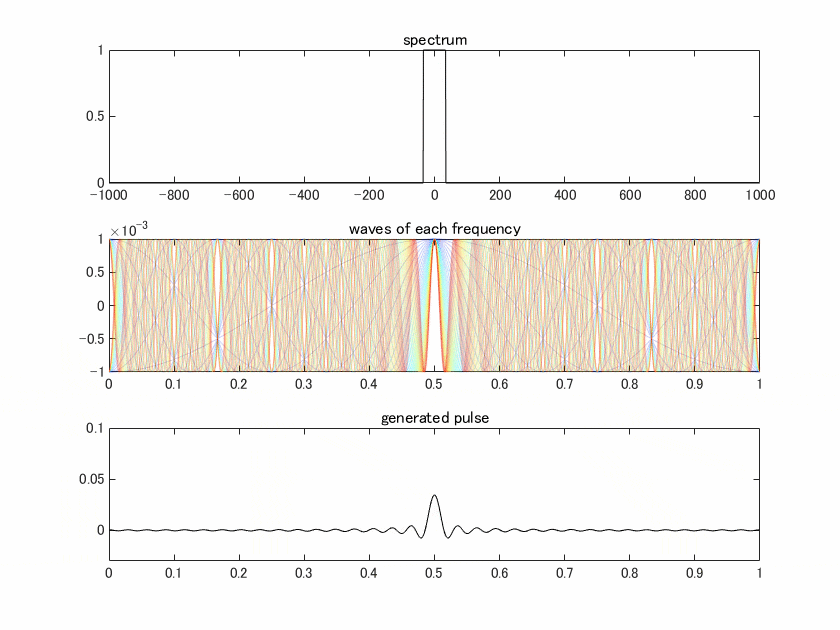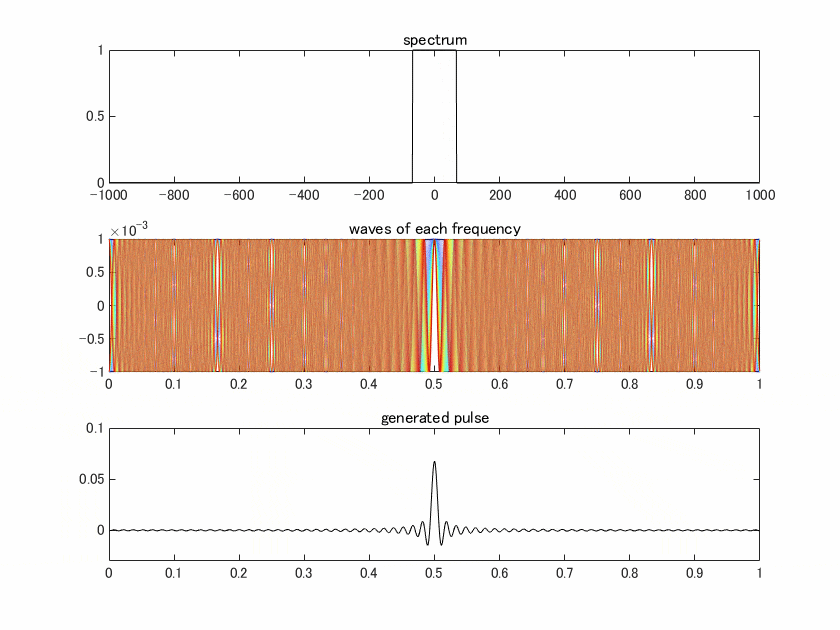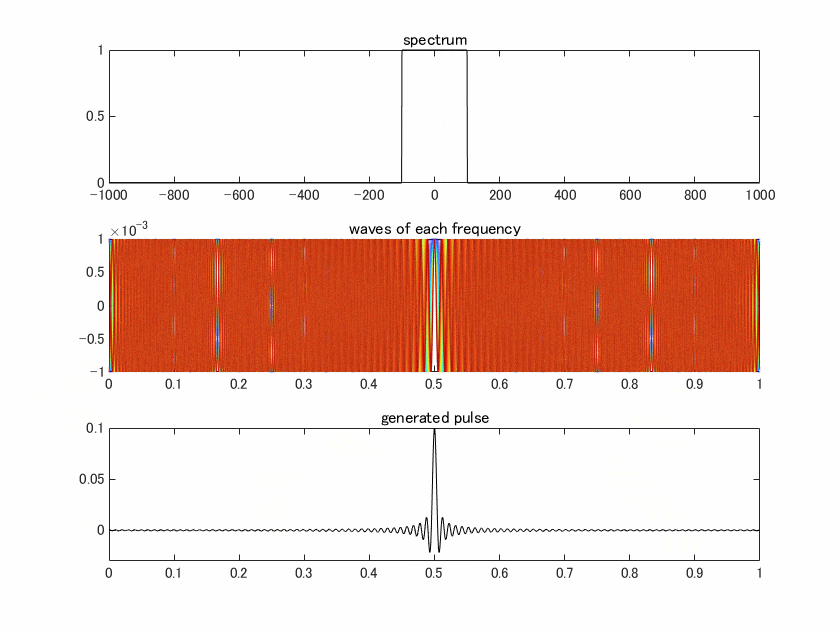
上の図はスペクトル、真ん中の図はスペクトルに含まれる各周波数の波を色付けして表示したもので、青から赤にかけて低周波→高周波、となっています。一番下の図はこれらの波を全部足し合わせた結果得られるパルス、ということになります。
真ん中の図で注目してもらいたいのは、時間0.5[s]ではすべての周波数で値が1（位相ゼロ）になっていて、他の時間ではそうなっていないということです。コードにもあるように0.5で位相ゼロになるように作ったからなのですが、様々な周波数が含まれた結果、それ以外の時間で全部の周波数が位相ゼロになるということはありません。なのでこの時間にだけ鋭いピークが立ちます。帯域が広がるほどこの効果が際立ってくるので、パルスは細くなっていきます。
信号処理をやってパルスを形成するさいには、「この位相をそろえて足し合わせる」ということが非常に重要になってきます。さて、ではチャープとは？

チャープも広帯域

先述のとおり、チャープは時間によって周波数を変えていくので様々な周波数が含まれる→広帯域な信号です。広帯域だけど全然鋭いパルスっぽくないのは各周波数の位相がずれているからなんですね。逆に言うと位相を揃えてあげれば鋭いパルスになります。これをしているのがマッチドフィルタということになります。マッチドフィルタは、時間領域で畳み込み積分に違いないわけですが、これの周波数での表現を覚えていますでしょうか。受信信号のスペクトルに参照信号のスペクトルの複素共役を掛けるだけです。複素共役を掛ける、ということは位相をキャンセルする、つまり位相を揃えるということですね。なので結果を逆フーリエ変換すると鋭いピークになるというわけです。
これもアニメーションで見ていきましょう。

チャープの位相を変えてsincパルスに変えるコード

clear, close all
prf = 0.2;
fs = 500;
bw = 200; % [Hz]
pw = 0.8; % [s]
df = prf;
f = [(-fs/2):df:(fs/2)-df]; % [Hz]
dt = 1/fs;
t = [0:fs/prf-1]*dt; % [s]
k = bw / pw; % chirp rate;
chirp = phased.LinearFMWaveform("PulseWidth", pw, "SweepBandwidth", bw, ...
    "SweepInterval", "Positive", ...
    "SampleRate", fs, "PRF", prf);

tc = pw/2; % pulse center time;

tsig = chirp();
fsig = fft(tsig);
fsig_phase= unwrap(angle(fsig));

target_phase = -2*pi*ifftshift(f')*tc;
cor_phase = target_phase - fsig_phase;

fig = figure;
filename = 'chirp_to_sinc.gif';
for i = 0:1:100
    cur_phase_unw = fsig_phase + cor_phase*i/100;
    cor_fsig = abs(fsig) .* exp(j*cur_phase_unw);
    shift_time = i/100*tc + (100-i)/100*f'/k;
    shift_time = shift_time(abs(f-bw/2)<=bw/2);

    subplot(2,1,1);
    yyaxis left;
    plot(f, fftshift(abs(cor_fsig)), 'b');
    set(gca, 'XLim', [0 200]);
    xlabel('Freq [Hz]');ylabel('Amplitude');
    yyaxis right;
    plot(f, fftshift(angle(cor_fsig)), 'r');
    axis([0 200 -pi pi]);
    xlabel('Freq [Hz]');ylabel('Phase [rad]');
    title({sprintf("chirp%s%s%ssinc", repmat('-',1,floor(i/5)),'|',repmat('-',1,20-floor(i/5))), "Spectrum"});

    cor_tsig = ifft(cor_fsig);
    subplot(2,1,2);
    p1 = plot(t, real(tsig), 'b');
    set(p1, 'Color', [0 0 1 0.1])
    hold on;
    p2 = plot(t, real(cor_tsig), 'r');
    axis([0 1 -3 14]);
    xlabel('Time [s]')

    cmap = jet(numel(shift_time));
    for ii = round(linspace(1, numel(shift_time), 100))
        plot([shift_time(ii) shift_time(ii)], [-3 -2], 'Color', cmap(ii,:));
    end
    grid on;

    hold off;
    drawnow;

    [A, map] = rgb2ind(frame2im(getframe(fig)),256);
    if i == 0
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.05);
    else
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.05);
    end
end

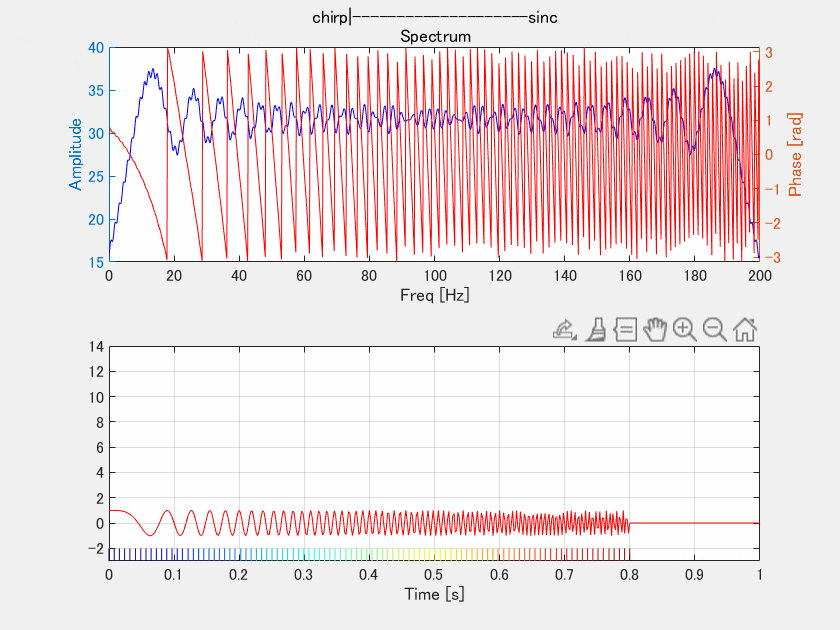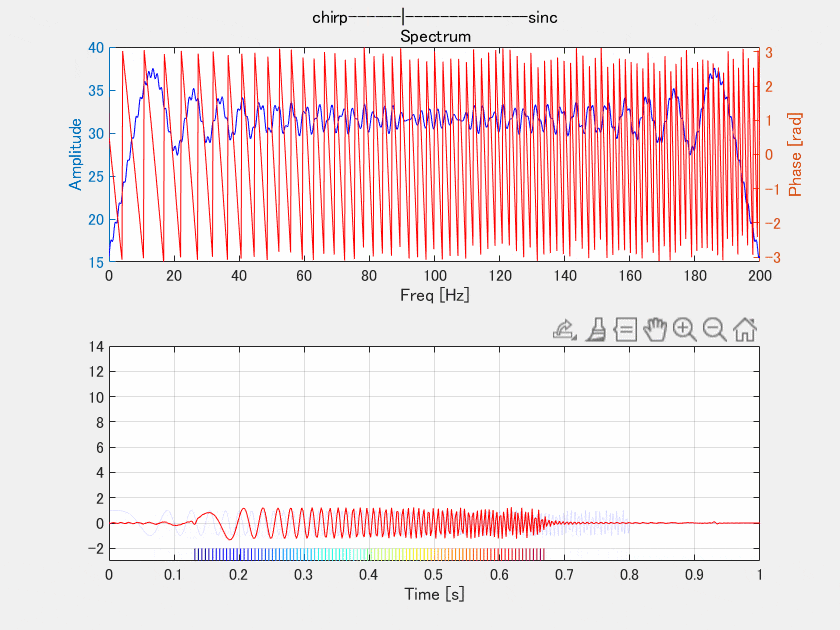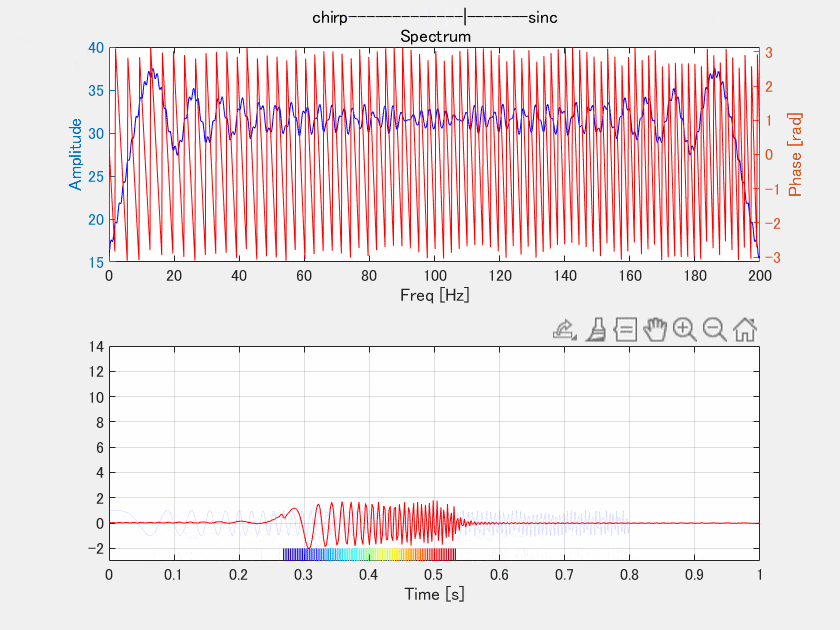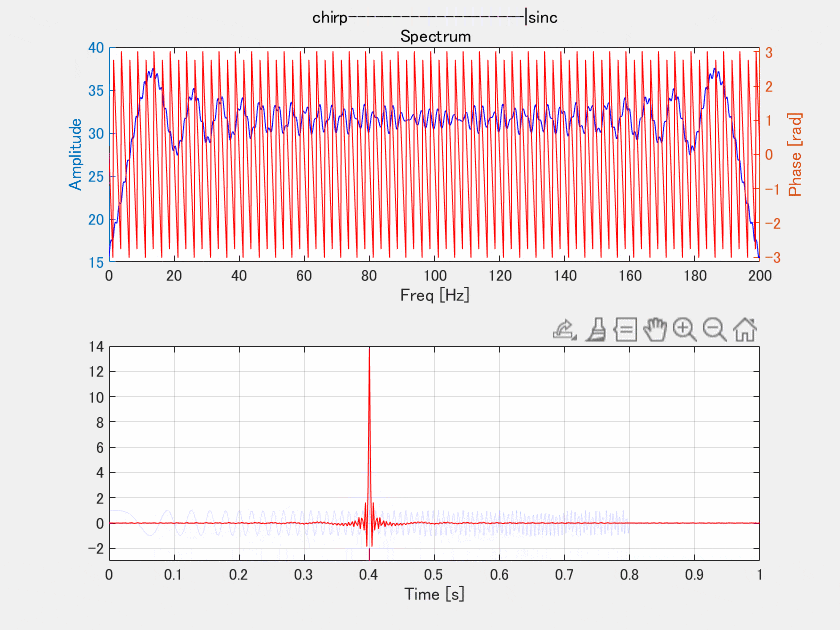
上はチャープの振幅スペクトルと位相スペクトルですが、ここでは位相スペクトルだけをいじって位相を揃えていきます。下の図は結果の時間信号です。チャープでは分散していた各周波数の位相を0.4[s]に向かって合わせました。
位相を揃えていく、とか言いながら位相スペクトルギザギザじゃないですか！これは0.4[s]に合わせているので求める位相は周波数に対して線形になります。よく見るとプロセスが進むにつれて位相は等間隔にのこぎり型になっていきます。
マッチドフィルタはこれを一瞬でやっているということですね。

おまけですが

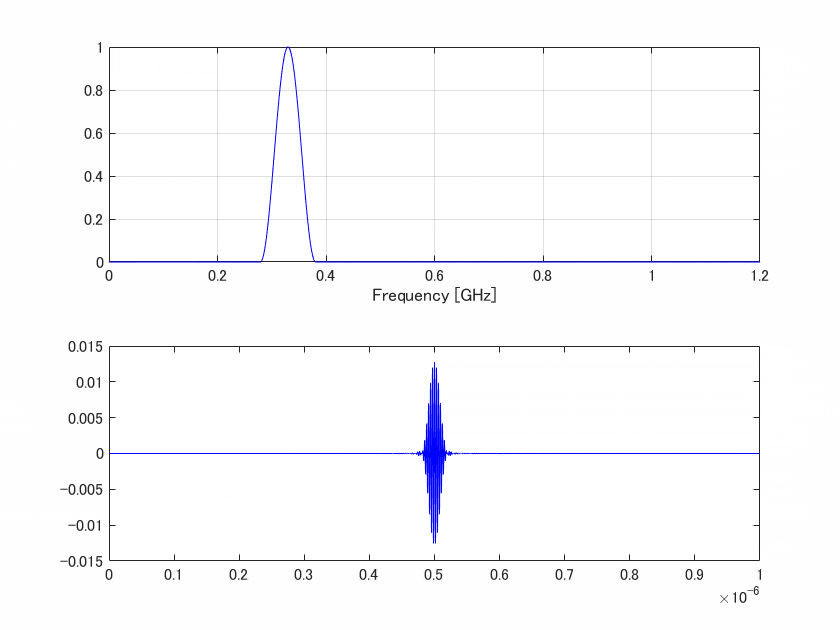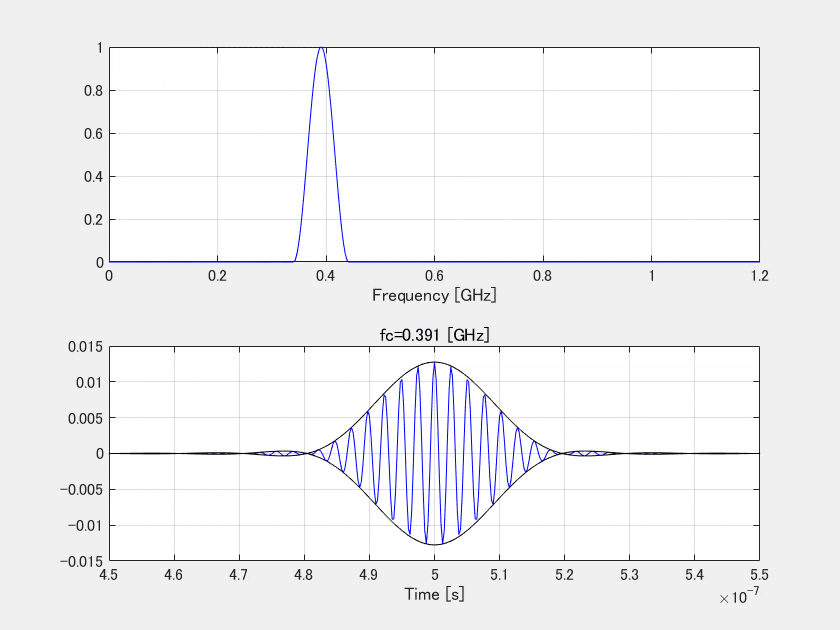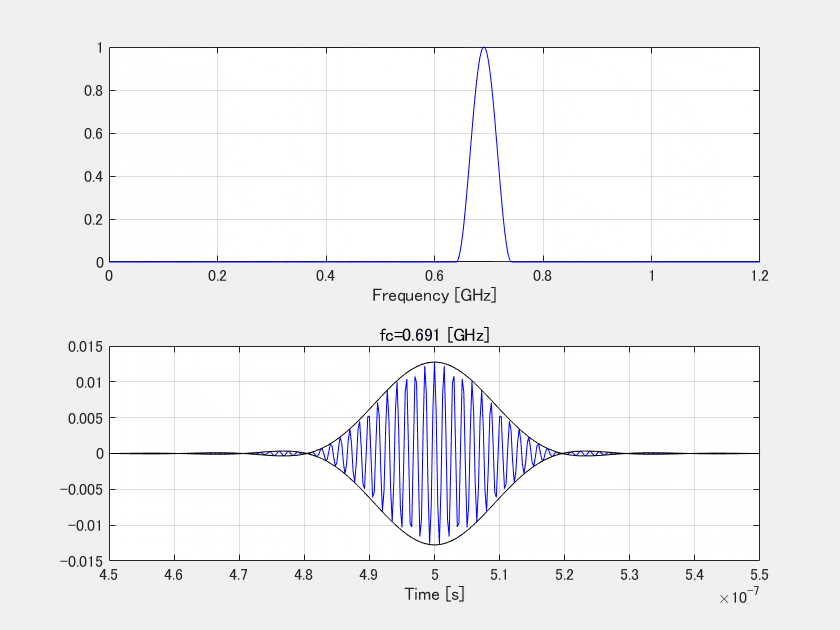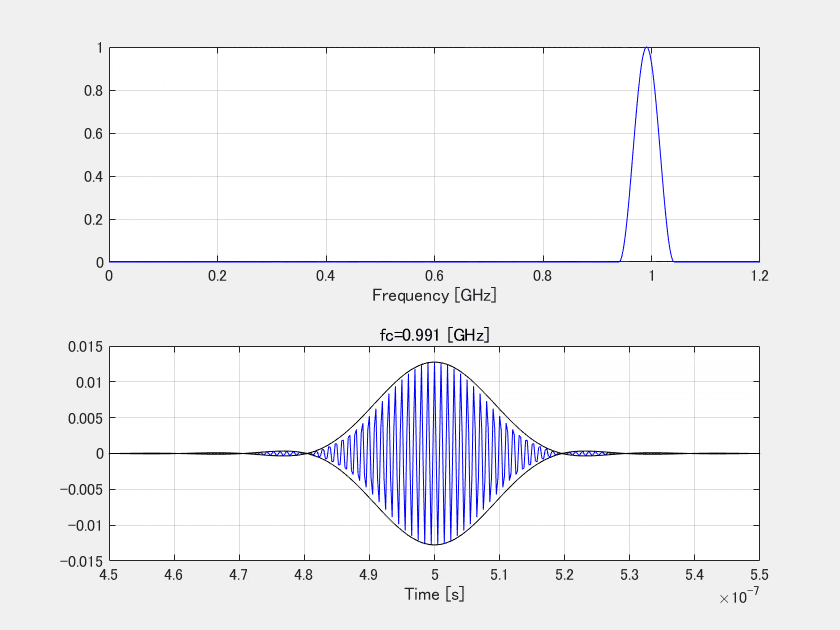
注意点として、よく高分解能（鋭いパルス）=高周波数と考える間違いがあります。あながち間違いでないんですが、間違いです。帯域を100MHzに固定して、中心周波数を高くしていきます。

中心周波数を変えて、パルスを見るコード

df = 1e6; % 1 MHz
freq = -2e9:df:(2e9-df);
dt = 1/4e9;
time = [0:numel(freq)-1]*dt;
BW = 1e8;

filename = 'fc_change.gif';
for fc1 = 1e8:df:1e9
    fsig1 = zeros(size(freq));
    fsig1(((fc1-BW/2)+2e9)/df+1:((fc1+BW/2)+2e9)/df+1) = ...
        hanning(BW/df+1)' .* exp(complex(0,-2*pi*[fc1-BW/2:df:fc1+BW/2]*0.5e-6));

    fig = figure(1);
    subplot(2,1,1);
    plot(freq/1e9, abs(fsig1), 'b')
    set(gca, 'XLim', [0 1.2]);
    xlabel('Frequency [GHz]')
    grid on;

    subplot(2,1,2)
    tsig1 = ifft(fftshift(fsig1));
    plot(time, real(tsig1), 'Color', [0 0 1]);
    title(sprintf('fc=%4.3f [GHz]', fc1/1e9)); hold on;
    xlabel('Time [s]');

    plot(time, +abs(tsig1), 'k');
    plot(time, -abs(tsig1), 'k');
    set(gca, 'XLim', [0.45 0.55]*1e-6);
    hold off;
    grid on;
    drawnow;

    if mod(fc1,1e7) == df % 10ステップごとにGIFに書き出す
        [A, map] = rgb2ind(frame2im(getframe(fig)),256);
        if fc1 == 1e6
            imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.1);
            fc1
        else
            imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.1);
            fc1
        end
    end
end

ご覧の通りエンベロープの中の波長は、スペクトルの中心周波数に応じて変化していきますが、レーダ分解能において重要なのはこのエンベロープの幅です。幅は、中心周波数でなくてただ帯域だけで決まります。
あながち間違いじゃない、といったのは、広帯域にしていくと自然と高周波成分が含まれることになるので、そういう意味では高分解能=高周波が必要、という意味ですね。まぁ何をもって高周波というのかは各ドメインにも寄るでしょうが…。

おわりに

今回アニメーションを目的にして信号処理を題材に作ってみました。作る過程で思い通りの結果にならないこともあったりして、久しぶりに信号処理の復習もできてよかったです。これからもできるだけアニメーションでコンテンツを作っていこうと思います。