※ 本記事は多くの言語に通用する普遍的な内容を志していますが、実験はpythonでしか行っていないため予めご了承ください
1. はじめに
先日 Atcoder という競技プログラミングサイトのコンテストにおいて、以下の問題が出題されました。
Atcoder Beginner Contest 175 E問題 Picking Goods
問題の詳細は記事の趣旨から外れるため省略します。
一言でいうと3次元の状態を管理する動的計画法の問題で、
愚直に実装すると最大で以下のような $3000 \times 3000 \times 4$ の3次元配列(リスト)を生成する必要がありました。
dp = [[[0]*4 for _ in range(3000)] for _ in range(3000)]
この配列の要素数は$4\times10^{7}$ 程度です。
その後の処理を含めても、この問題の実行時間制限3secに対して計算量的には問題ありません。
ところが、筆者が使っているpypy(高速化版python)という言語ではなぜかTLE(実行時間超過)してしまいました。
python系が遅いからというのもありますが、それ以外の多くの言語でも同じように実装すると実行時間が長くなると思います。
コンテスト後に正解者のコードを見て原因を考えていたところ、この現象を回避するには
- 一番外の次元を使い回して2次元配列を保持する(動的計画法ならではのテクニック)
- 次元の順番を工夫する
などの工夫が必要であることが分かりました。
このうち2次元にすれば早くなるのは直感に反しませんが、
次元の順番を変える方は計算量が変わらないので不思議ですよね。
なぜこのようなことが起きるのでしょうか?
結論から言うとメモリアクセススピードが関係しているのですが、
本記事ではこの現象について、実験を通じた検証と理論的背景の説明を行いたいと思います。
色々調べてみるとここら辺の高速化の話は熟練技が多いですが、今回の話はそんなに複雑ではなくコンテスト中でも簡単に意識できるものですし、ピンポイントな解説記事が見つからなかったので記事にしました。
筆者が普段pythonを使っているため実験にはpythonを用いますが、
この記事のテーマは決してpython高速化ではなく、多くの言語に共通する話なので、
pythonista以外の方にもぜひ読んでいただきたいです。
2. 実験
今回の問題で必要となるような$3000\times 3000\times 4$の配列を、次元の順番を変えながら生成して速度を比較します。
なお、$A[N][M][L]$と書いた場合、pythonを使って以下のようなコードでリストを生成していると思ってください。
A = [[[0]*L for _ in range(M)] for _ in range(N)]
Atcoderのコードテストで時間を計測したところ、以下のような結果となりました。
| 配列形式(3次元) | python | pypy3 |
|---|---|---|
| $A[4][3000][3000]$ | 649ms | 289ms |
| $A[3000][4][3000]$ | 616ms | 287ms |
| $A[3000][3000][4]$ | 5547ms | 2029ms |
なんと、pythonの場合もpypyの場合も、最内次元の要素数を4とした場合に実行時間が10倍近くになってしまうことが分かりました。
ついで、全体の計算量を大きく変えないようにしながら2次元と4次元でも同様の実験を行ってみました。
| 配列形式(2次元) | python | pypy3 |
|---|---|---|
| $A[4][10^{7}]$ | 431ms | 238ms |
| $A[10^{7}][4]$ | 5937ms | 3097ms |
| 配列形式(4次元) | python | pypy3 |
|---|---|---|
| $A[4][200][200][200]$ | 774ms | 278ms |
| $A[200][4][200][200]$ | 784ms | 279ms |
| $A[200][200][4][200]$ | 960ms | 303ms |
| $A[200][200][200][4]$ | 4634ms | 1759ms |
これらの場合も傾向は同じで、最内次元の要素数を4とした場合に実行時間が極端に長くなっています。特に、2次元の場合は10倍以上の差がついています。
次の章で理由を説明しますが、
実は計算量が同じ場合**「全体の要素数 ÷ 最内次元の要素数」によって実行時間が大きく変わります。
最内次元以外の要素数の積と考えても同じです。
つまり$A[N][M][L]$の場合、$N\times M\times L$が同じなら一番内側の$L$が大きいと速く、小さいと遅く**なります。
そのため、$A[4][3000][3000]$と$A[3000][4][3000]$は最内次元がどちらも3000なので実行時間に大差がなく、$A[3000][3000][4]$だけ極端に時間がかかってしまうのです。
実用上はこれで十分かと思いますが、次の章でなぜそうなるか説明していきます。興味のある方は読んでみてください。
3 理論的背景
3-1 多次元配列のメモリレイアウト方式
まず前提として多次元配列のメモリレイアウト方式について理解する必要があります。これに関しては、以下の記事が参考になります。
この記事によると、競技プログラミングのメジャー言語であるC++, python, Java, C, C#などの言語においては「Row-major order方式」または「Iliffe vector を用いた方式」が採用されています。
この2つの方式の共通点は、二次元配列$A$において$A[i][j]$と$A[i][j+1]$のような同じ行の値は隣接するメモリに格納されるが、$A[i][j]$と$A[i+1][j]$のような同じ列の値は離れた場所に格納されるということです。このため、同じ行の値に順にアクセスするとシーケンシャルアクセス1ができ、実行時間を短縮することができます。
3次元以上の場合どうなっているのか調べた限りではよく分からなかったのですが、おそらく最内次元のインデックスのみが異なる要素同士、$A[i][j][k]$と$A[i][j][k+1]$が隣接して格納されていると考えられます。
3-2 参照の空間的局所性
先ほどのメモリレイアウト方式の説明で、シーケンシャルアクセスができると速くなるという説明をしました。このようなアクセスは**「データの空間的局所性を上手く利用している」**ということができます。逆に言うと、データの空間的局所性を上手く利用して配列にアクセスできれば、実行時間が短縮されるというわけです。
これに対し、シーケンシャルでないアクセスはランダムアクセス2となり、アクセスに時間がかかってしまいます。
局所性の概念についてはこれ以上深掘っても仕方ないのでこれぐらいにしますが、さらに興味のある方は以下のWikipediaの記事を読んでみてください。行列積の例がとても面白いです。
3-3 ランダムアクセスを減らすには
実際に多次元配列を生成する場合、次元の順番をどうしようとトータルのアクセス回数は変わらないのですが、ランダムアクセスとシーケンシャルアクセスの割合が変わります。
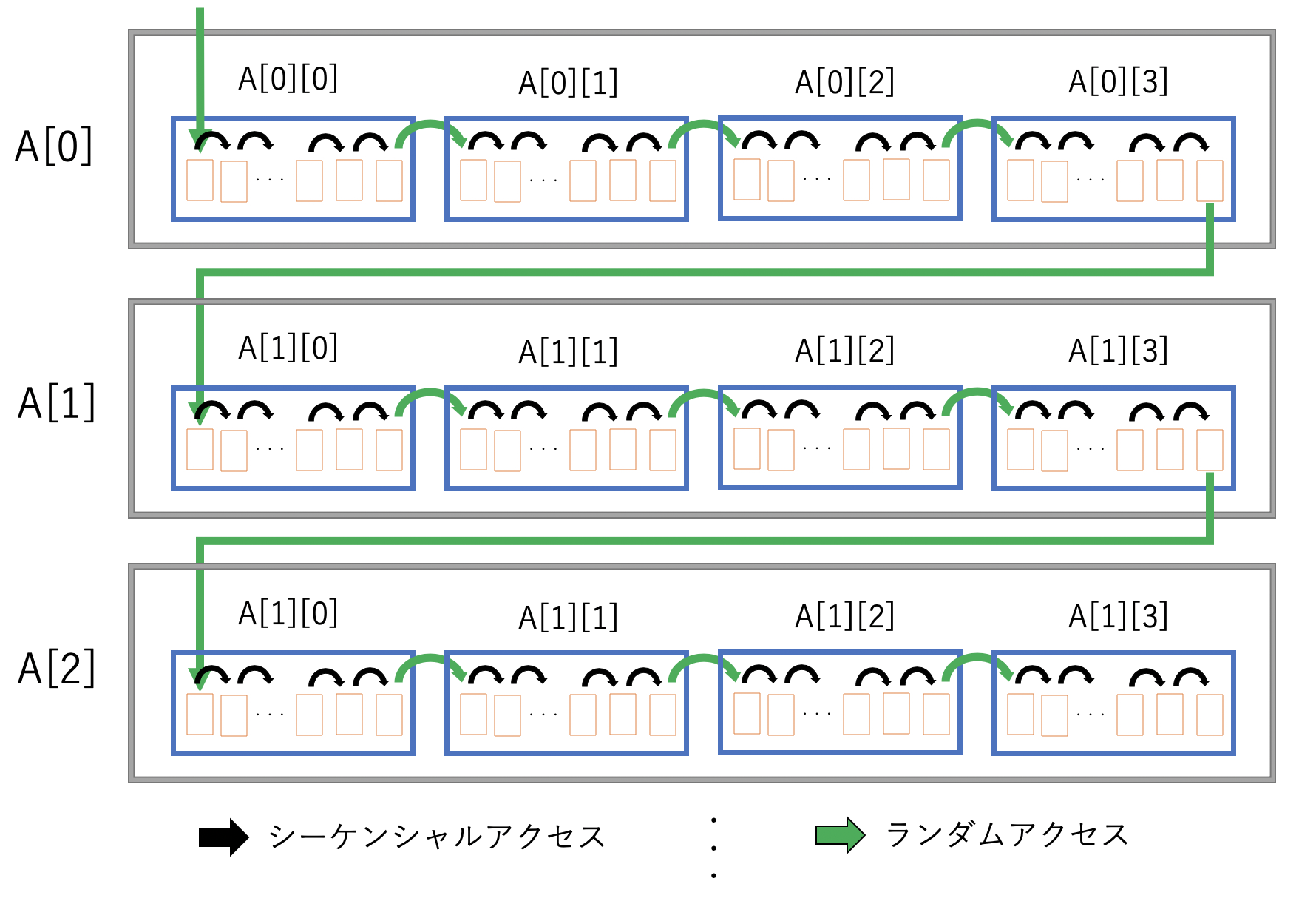
ランダムアクセスの回数がどのように決まるのか考えるため、3次元配列を以下のような図で表して考えてみたいと思います。
この図は全体が$A$という配列を表しており、$A[0][0][0]$から$A[-1][-1][-1]$まで順番にアクセスするときの様子を矢印で表したつもりです。アクセスされる各データが箱で表されています。この時、同じ青い箱の中にあるオレンジの箱同士は隣接するメモリに格納されているため、シーケンシャルアクセス(黒い矢印)することができますが、青い箱を出入りする際にはランダムアクセス(緑の矢印)になってしまいます。
今、緑の矢印(=ランダムアクセス)が何個あるかを考えたいのですが、図をよく見ると、これは青い箱の総数に等しいことが分かります。よってこの青い箱の総数を減らすことができればランダムアクセスが減り、アクセススピードを早くすることができます。
$A[N][M][L]$という配列を考えたとき、青い箱の総数は$N\times M$個、すなわち最内次元以外の要素数の積です。
以上より、最内次元以外の要素数の積が少ない方がメモリアクセススピードが早くなることが分かりました。
4. おわりに
長くなりましたが以上です。
まとめると、「二次元以上で、ある次元の要素数が非常に少ない配列」を扱う場合、計算量だけでなくメモリアクセススピードがボトルネックになってしまう可能性があり、次元の順番に注意が必要になります。
筆者自身このことをあまり意識していなかったため、今回のコンテストでは時間内に正解することができずに痛い目を見てしまいました。まあ、DP配列の使い回しをちゃんとやれという話なんですけどね。
普段でも、配列を2本用意すればいいところを何の気なしに最内次元を2にして1つの配列で済ませてしまうなどはやりがちなので、意識しておく価値はあると思います。
サイズが小さい配列なら何の問題もないですが、ある程度大きい配列の場合には大きく影響するかもしれません。
記事の内容に関してはしっかりとリサーチをしたつもりですが、特に理論的背景の部分は完全に正確ではないと思いますので、何か明らかな間違いがあればコメント等でご指摘いただけると幸いです。
また、この記事の執筆にあたっては研究室の後輩君に理論的背景の部分の教えを乞い、さらに完成した記事にもアドバイスを頂きました。加えて、このような教育的な問題を作ってくださったAtcoderのWriterの方にもこの場を借りて感謝させていただきます。