松尾研究室が提供している講座、Deeep Learning基礎講座 https://deeplearning.jp/lectures/dlb2018 を受講中です。数式と実装のところで分からなかった人が、同じレベル感の人を対象に記事を書きました。一緒に基礎から復習しましょう!
講座自体は、ディープラーニングのライブラリを使えるレベルではなく、論文を読んで実装する、ライブラリを作る側にまわることを目標としたものです。第1回は「人工知能は人間を超えるか」に載ってるジェネラルな内容と受講者のTLで共通認識。割愛。第2回からハードになるので頑張りましょうとのことでしたが、本当にハードなので嘘偽りないです泣
以下自分が分からなかったことのまとめなので、一般的なことは省きます。
第2回 講義まとめ
- 機械学習(ML)の手法一覧
- 教師(あり|なし)学習、強化学習など
- MLのPipeLine
- input -> 特徴ベクトル -> 特徴抽出 -> output
- 特徴空間
- 類似度とかわかる
- 決定(境界|領域)
- 分類器で分けられた部分空間
- モデルの評価
- 評価方法は精度、再現性、F値、正解率で決まる
- 検証方法
- ホールドアウト、交差検証がある
- ここから具体的な手法、そして実装へ
- ロジスティック回帰
- ニューラルネットの単純な構造
- 単純パーセプトロンとモデルは同じ
- 重みとバイアスを勾配降下法で決定するよ
- 活性化関数、シグモイド関数、尤度関数、交差エントロピー誤差関数、勾配降下法、ソフトマックス関数、、^^
- ロジスティック回帰
- 演習
- ロジスティック回帰、ソフトマックス回帰
参考書など
公式で紹介しているのはこの2冊
1冊目高いわ!と思ったら、原書のHTML版が無料で見られるぽいです。私はお金ないのでこれで頑張ります。 -> https://www.deeplearningbook.org/
その他
- https://www.commonlounge.com/discussion/367fb21455e04c7c896e9cac25b11b47 -> 少ない説明でざっと全体をやるのを目的としたサイト。統計と機械学習, Pythonライブラリ練習に超おすすめ。超やってる。
ロジスティック回帰を理解する。
ここからは置いてきぼりを食らった後半を、復習します。途中で口調変わります、すみません汗
まず、ロジスティック回帰で成し遂げたいことは、データをラベル付けして分けることです。多クラス分類は、データセットをクラスごとに分類します。最終的にテストデータをあるクラス $C_k$になる確率$p \in [0,1]$を表すのに、ロジスティック関数を使います。ここでは、単純のため二値分類を考えます。
単純パーセプトロン
二値分類は、例えば画像認識で犬か猫で分けたい時、データセットが犬と猫しかないと仮定したら、犬か犬でない、True or Falseで判断すればいいのです。ロジスティック回帰に似てもっと単純なモデル、単純パーセプトロンを図式化してみます。
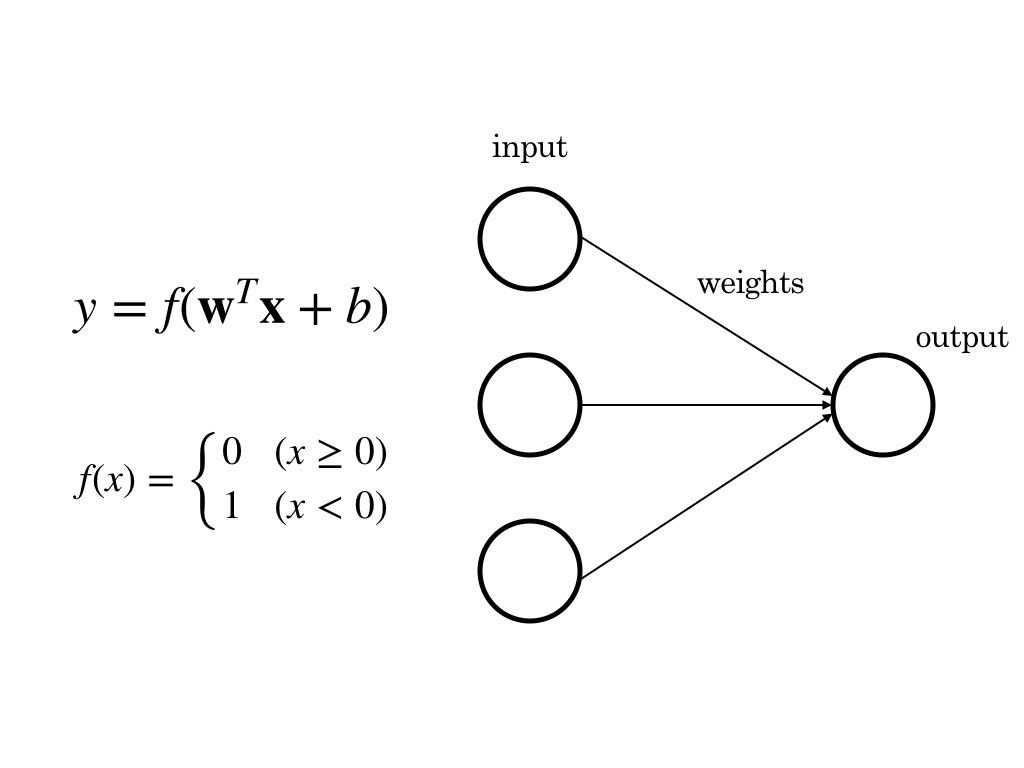
※ $\mathbf{x}$ is input,$\mathbf{w}$ is weights, $y$ is output.
活性化関数
単純パーセプトロンは活性化関数として$x$によりyが0か1に決まる、上のような定義の関数$f(x)$(ステップ関数という)を使っています。活性化関数とは、input, weights, bias ( $\mathbf{w^Tx}+b$ ) に対して、最終的にoutputを決める関数のことです。つまり、発火するかしないか。このモデルは脳神経を模していて、inputがあるとき一方のニューロンが他方に対して発火するかしないかをweightによって決める様を表しています。ロジスティック関数では発火する確率を求めます。同じくoutputは[0,1]区間に収まりますが連続な関数を使います。
ロジスティック回帰
ロジスティック回帰を実現するロジスティック関数は、inputがあるクラス$C_k$になる確率を返します。関数の形から、シグモイド関数とも言えます。
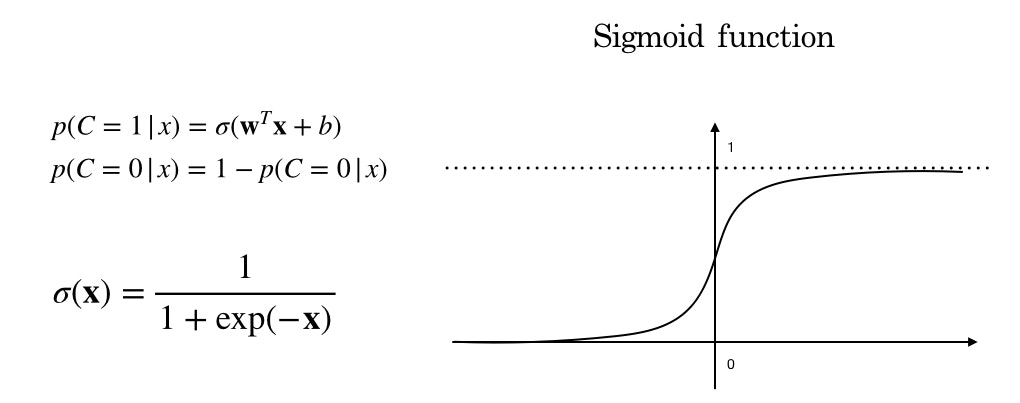
ここで、$C=1$はある条件がTrueになる、つまり犬になる場合です。$C=0$はfalse 犬でない場合です。ここまでで、ロジスティック回帰の目的である、二値分類を確率によって実現できました。
Weightsとバイアスを学習により求める
ここまでで、inputをモデルに突っ込めば犬か猫か分けられるようになったようですが、肝心のモデルはどうやって作るか?詳しく言えばweightとバイアスはどう設定するか?の疑問に答えていません。このパラメータ(weight, biasのこと)を設定を機械にやらせようというのが、機械学習なのです。
大まかにいうと、トレーニングデータセット(正解つきデータ)を入力して、尤度関数を最大化させるようなパラメータを求めます(最尤推定)。
尤度関数
尤度関数とは、全ての事象が起きる確率を掛け合わせたもの。最尤推定は、尤度関数の最大値となるパラメータを推定することである。
学習データについて考える。ある犬に近い画像が、犬とラベルつけられている。これは、C=1を表す。この時わかってるのは、画像と確率変数Cの値のみであり、確率はわかっていない。この画像をモデルが犬と判断するにあたり、確率を最大限に高める必要がある。これを全学習データ分考える。つまり、それぞれの事象$\mathbf{x}_i$が犬(C=1)、もしくは猫(C=0)になる確率を最大限高める(つまり全部掛けた値が最大になる)のが最尤推定である。
式を見よう。N個の学習データと正解ラベル$(\mathbf x_i,t_i) \in X$, $t \in \{0,1\}$に対して尤度関数を定義すると
L(\mathbf{w},b) = \prod_{ (\mathbf x_i,t_i) \in X }^N p(C=t_i \mid \mathbf{x}_i)
ここからどうやって、最尤値時の$(\mathbf{w}, b)$を求めるのか。アイディアは簡単で、尤度関数の各パラメータについて偏微分して0になる値を探せばいい。しかし、解析的にそれを解くのが難しいから、対数を取り、コンピュータで近い値を導く。それが勾配降下法である。
勾配降下法
まず、先ほどの尤度関数の対数をとって符号を反転させた、交差エントロピー誤差関数を定義する。
\begin{align}
E(\mathbf{w},b) &= -\log L(\mathbf{w},b)\\
&= -\sum p(C=t_i \mid \mathbf{x}_i)\\
\end{align}
なぜ負の値をとったのかというと、関数の最小値をとるパラメータを見つける、勾配降下法で便利だからである。このように、関数の最小値を求めることを、最適化という。
勾配降下法のアイディアは、あらかじめ初期パラメータを決めてしまう。そこから尤度関数の偏微分した値に学習率$\eta$を掛けたものを引いていく、この動作を再帰的に繰り返し、パラメータの収束値を求める。
\mathbf{u}^{(k+1)} = \mathbf{u}^{(k)} - \eta \frac{\partial E}{\partial \mathbf u}\\
\mathbf u = \{\mathbf w, b \}
実装
は、演習用notebookをみてください。。(ここで力尽きる)
講座を受けてない人も演習用コンテンツは公開されているので、試してみてください!
多クラス版ロジスティック回帰
活性化関数にソフトマックス関数を使い、データがそれぞれのラベルに分けられる確率を求める。正解データにはOne-hotベクトル表現を用いる。
宿題を実装する
近日中
参考文献
http://darden.hatenablog.com/entry/2016/08/22/212522
http://darden.hatenablog.com/entry/2018/01/25/222201
http://gihyo.jp/dev/serial/01/machine-learning/0016
http://gihyo.jp/dev/serial/01/machine-learning/0018
http://sinhrks.hatenablog.com/entry/2014/11/24/205305
http://tkengo.github.io/blog/2016/06/04/yaruo-machine-learning5/
https://mathtrain.jp/mle