以下の記事は自身のブログData Science Struggleでも掲載予定。許可なき掲載とかではない。
概略
深層学習における技法の一つであるDropout(ドロップアウト)についての論文を読んだので、その仕組みを簡単にまとめる。
Dropoutに関する論文を読んだのだが、最近読んだ論文の中だと地味に実践に活かせるエッセンスが多く、個人的に得るものが多かったのでまとめておきたくなった。
Dropoutとは?
Dropoutとは、ニューラルネットワークの学習時に、一定割合のノードを不活性化させながら学習を行うことで過学習を防ぎ(緩和し)、精度をあげるために手法。
ニューラルネットワークは訓練データに対するトレース能力に優れており、わりと簡単に過学習を起こしてしまうため、正則化やDropoutのような手法を用いることは重要である。
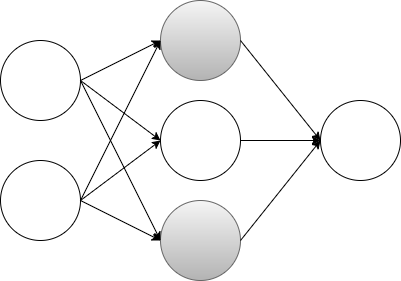
具体的なDropoutのイメージは以下の図のようになる。
上記図の、色のついたノードが不活性化されている。
学習時に特定のノードを不活性化させて、学習を進めていくことで、過学習を抑えながらパラメーターの更新を行える。
論文を参考に具体的に見ていく
Dropoutによって得られる効用は以下の二つ
- 過学習の緩和
- 複数モデルの組み合わせによる精度の向上
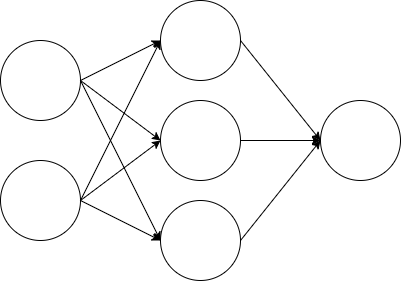
具体的に以下の、入力層、隠れ層、出力層の3層からなるニューラルネットワークを考える。
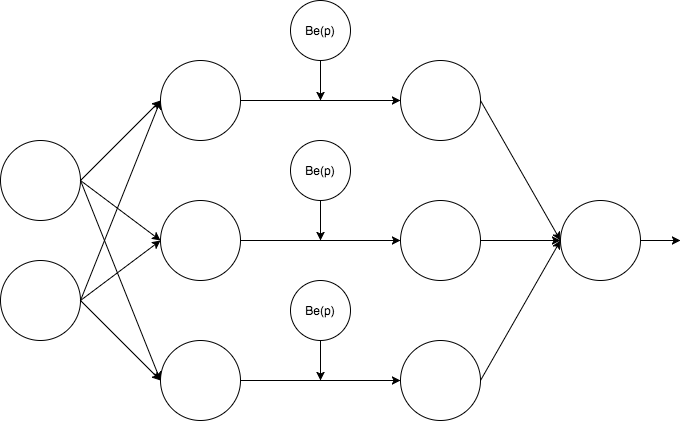
この隠れ層にDropoutを仕込むと図では以下のように表すことができる。$Be\left( p \right )$と記されているノードがDropoutを表している。この図からわかるように、Dropoutによる不活性化の選択はDropoutを仕込んだ層の各ノードごとに対してなすことになる。
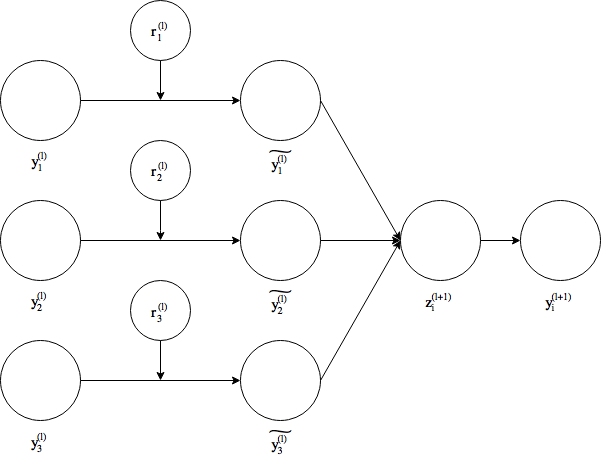
数式で説明することを意識して図をより正確に描く。
当該レイヤーのうちの指定割合だけノードを活性化させるのではなく、各ノードが活性化する確率が与えられる。上記の図を数式で表す。
$r_j^{\left( l\right) }\sim Bernoulli\left( p\right)$
$\tilde{y^{\left( l \right)}} = r^{\left( l \right)} \times y^{\left( l \right)}$
$z_i^{\left( l + 1 \right)}=w_i^{\left( l+1 \right)}\tilde{y^l}$
$y_i^{\left( l+1 \right)}=f\left(z_i^{\left( l + 1 \right)} \right)$
この式の$r$の部分が具体的にDropoutを表している。レイヤー内の各ノードに設置され、その値はベルヌーイ分布に従う。つまり、確率$p$で$1$,$1-p$で$0$となる。
この場合は、$y_{i}^{\left( l\right) }$が確率$p$でそのまま次のノードの入力値となり、確率$1-p$で$0$を次のノードに与える。
訓練時にはこのように、活性化されたノードと不活性化されたノードを持つ状態でパラメーターの更新を行い、テスト時には、そのパラメーターに上記で指定した$p$を掛ける。式で書くと$W_{test}^{\left( l\right) }=pW^{\left( l\right) }$となる。
『複数のモデルの組み合わせ』とは要するに、訓練時に活性化してるノードによってできる異なるネットワークによる組み合わせのこと。$n$個のノードがある場合は$2^{n}$個のネットワークができうる。それらのネットワークでパラメータが更新されるため、『複数ネットワークによるパラメーター更新』となっている。
Dropoutのパラメーター調整
Dropoutは調整パラメーター$p$を持つ。この$p$の調整を行うとき論文内で試されていたのは以下の二つの設定。
- そのレイヤーのノード数を固定してDropout率をいじっていく
- そのレイヤーのノード数を$n$としたときに$p \times n$を一定値に固定して$p$と$n$をいじっていく
一つ目の『そのレイヤーのノード数を固定してDropout率をいじっていく』というのは訓練時に活性化するノードの数をパラメーターで変化させて、AccuracyやLossを観測していく。二つ目の『そのレイヤーのノード数をnとしたときに$p \times n$を一定値に固定して$p$と$n$をいじっていく』というのは訓練時に活性化するノードの数を固定して、パラメーターを変化させて、AccuracyやLossを観測していく。
実際にDropout以外の要素を固定して実験をしてみると、活性化しているノードが少ないと、データを食わせてもなかなか学習が進まないことが多い。かといって、活性化しているノード数が不活性化してるノード数に対して多過ぎれば容易に過学習が観測された。上記の二点の観点からDropoutのパラメーターを調整するのが実践的なのだろう。
また、おおよその目安として、inputを行った直後のDropoutは80%程度のノードが活性化されているのが好ましく、隠れ層は50%前後が活性化しているのが良いらしい。
感想
個人的には以下の点が気になった、もしくは発見だった。
- Dropoutのパラメータ$p$が、レイヤー単位ではなくノード単位に課せられているという点は知らなかった
- 論文ではDropoutのパラメータ$p$がactive nodeの割合パラメーターになっているが、Kerasだとdeactivated nodeの割合なのでKerasユーザーは論文を読むとき注意
- 言われればそうだが、Dropoutによりスリム化されたネットワークを組み合わせたことにより『複数モデルの組み合わせ』と考えたことはあまりなかった
参考論文
Geoffrey E. Hinton氏のページから閲覧可能なDropoutに関する論文。
論文内では、複数のデータセットに対してDropoutを仕込んだ時とそうでない時の精度の比較なども行われており、読んでおく価値は十分にある。