Stan Advent Boot Camp 第6日目 t検定が気になる

この記事はStan Advent Calendar 2020の6日目の記事です。

2020年12月9日に一部記事を下記の通り修正しました。
simizu706さん，ご指摘ありがとうございました。

• パラメタ制約と事前分布を修正し，結果も修正。
• Stanにおけるパラメタ制約に関する記述を追加。

t 検定をStan(rstan)でやってみよう。

Stan Advent Boot Camp 6日目へようこそ。
皆さん，順調にMCMC(*´Д`)ﾊｧﾊｧしていますか？

今日のテーマは帰無仮説検定の中でも馴染み深いであろう，t 検定です。
と言いつつ，この記事ではt 検定をrstanで行うというよりも，t 検定の代わりにモデルで考えてみよう，という趣旨の内容になっています。
勉強不足な点が多々あると思いますので，皆さんからいろいろご指摘いただければ幸せます。
なお，私のR力・Stan力は高くない上，アドカレ参戦も初なので緊張しております(;´Д｀)

今日のお品書き

• t 検定の考え方
• 一標本t 検定
• 対応のないt 検定
• 対応のあるt 検定

t 検定の考え方

"2群の平均値の差の検定"として，一度は触れたことがあるかと思います。説明は不要かもしれませんが，大まかにまとめると，t 検定には以下のバリエーションがあります。

種類	目的	例
一標本	母平均と任意の値との差	睡眠時間が日本平均より長いか
対応のない	独立な２つの母平均の差	2グループ間の睡眠時間の差
対応のある	対応のある２つの母平均の差	快眠方法教示前後の睡眠時間の差

いきなり母平均～なんて書きましたが，t 検定では母集団が正規分布に従っていると仮定，つまり，データが正規分布から生成していると仮定と言い換えることができます。
お察しのとおり，キャンプ3日目hirakawamakotoさんの「平均値を推定してみよう」の内容を活用できる(そのまま利用できちゃう)という訳です！
まだ読んでいない，という方は是非先に読まれることをお勧めします。

一標本t 検定

基準とする値とデータの平均値の差を考えたいときに使うのが一標本t 検定です。
ここでは，社員さん20名の睡眠時間が日本平均と差があるかを知りたいとします。手元には社員さんの睡眠時間データと，日本平均の約7.03時間という基準があるとしましょう。
なお，日本の平均睡眠時間はOECDの調査結果(2016)から引用しました。
(ちなみに，OECD調査国の中では一番短いです)

社員さん20名の睡眠時間データ

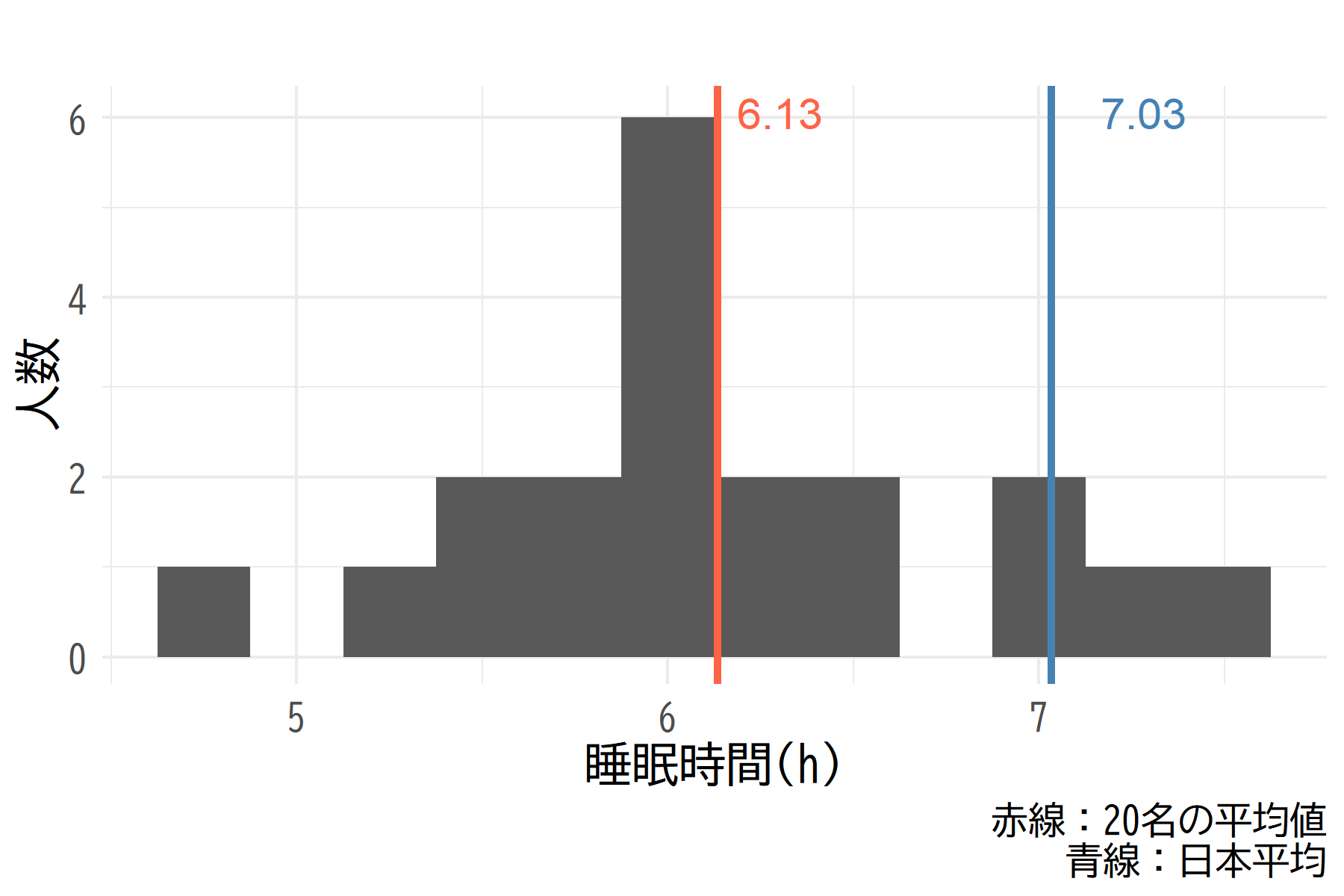
どうやら社員さん20名の睡眠時間は日本平均より短そうです。
また，平均を中心として概ね左右対称に見えますね。
では，どのくらい短いのか，日本平均との差をモデルとして考えてみましょう。

モデルを考える

まず，シンプルに社員さんの睡眠時間の生成過程を考えてみましょう。
色々突っ込みはあるかとおもいますが，社員さんの睡眠時間が正規分布に従っていると仮定すると，以下のように表現できます。

$Time[i] \sim Normal(mu_{社員}, sig)$

このまま推定すれば，社員さんの睡眠時間の平均$mu$(と標準偏差$sig$)は推定できますが，日本平均からどれくらい差があるのかは直接わかりません。
実際には平均値を推定するだけで十分だと思いますが，ここではあえて，任意の値との差を直接推定したいと思います。
どう考えるかというと，単純に日本平均をモデルに組み込みます。

$Time[i] \sim Normal(mu_{日本}+diff, sig)$

要は，社員さんの睡眠時間が日本平均$mu_{日本}$+差$diff$を平均とした正規分布から得られていると仮定するということです。
めっちゃシンプルですね。

モデル

下記モデルをmodel1.stanとして保存します。

一標本t検定stanモデル

data {
    int<lower = 0> N; //データ総数
    real<lower = 0> Time[N]; //社員さんの睡眠時間
    real<lower = 0> Japan; //日本平均
}

parameters {
    real<lower = -24, upper = 24> diff; //日本平均との差，パラメタの探索範囲を制約
    real<lower = 0> sig; //標準偏差
}

model {
    //モデル
    for (n in 1:N) {
        //日本平均に差が加わって社員さんの睡眠時間が生成
        Time[n] ~ normal(Japan + diff, sig); 
    }
    //事前分布
    diff ~ normal(0, 12); //-24~24時間を意識した事前分布
    sig ~ cauchy(0, 5); //裾の広い事前分布
}

任意の値である日本平均値をデータ(Japan)として与えること，推定するパラメータとして差(diff)を定義している部分が，一般的な平均値推定モデルと異なります。
なお，差の事前分布については，日本平均約7時間からのズレなので，かなり狭くしています。

推定

データの準備からMCMCまで一気にいきます。
なお，tidyverseは推定結果の可視化に使います。

パッケージ読込～MCMC

#パッケージ読込
library(rstan)
library(tidyverse)
#魔法の呪文
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
#睡眠時間データ
time = c(5.447781, 6.694716, 5.277793, 6.508100, 5.338882, 6.603984, 6.673767, 6.314401, 6.214725, 6.846517, 7.172932, 5.762782, 3.753255, 5.876118, 4.966249, 5.066775, 5.226231, 5.803360, 5.870738, 7.467991)
#Stan用のデータセット
data1 = list(N = length(time), #データ総数
             Time = time, #睡眠時間データ
             Japan = 422/60 #日本平均
             )
#モデル1をコンパイル
model1 = stan_model(file = "model1.stan")
#MCMC
fit1 = sampling(model1,
                data = data1,
                chains = 4,
                iter = 4000,
                warmup = 1000
                )

推定結果

視覚的チェック等の収束判断は省略します。

fit1の実行結果の一部

      mean se_mean   sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
diff -0.90    0.00 0.16 -1.22 -1.01 -0.90 -0.80 -0.58  8531    1
sig   0.73    0.00 0.13  0.53  0.64  0.72  0.80  1.03  8121    1

差*diff*の事後分布の期待値(EAP)も中央値(MED)も-0.90，つまり，概ね54分ほど日本平均より社員さんの睡眠時間は短いようです。
続いて，95％確信区間(事後分布の2.5%点から97.5%点)を見ると，-1.22 ~ -0.58となっており，確信区間の上限値が0未満であることから，日本平均との差は少なく見積もっても約34分はありそうだと考えることができます。

t 検定と異なるのは，このように差のとりうるであろう範囲を得られる点です。仮に，差の95%確信区間の上限値が0.5であれば，仮に事後分布の期待値が0未満であっても，差がほぼないと考えることができるでしょう¹。

事後分布の確認

実際のMCMCサンプルも確認してみましょう。

事後分布の可視化

#まだ読み込んでない場合
library(tidyverse)
#可視化のためにfit1からデータを取り出す
fit1data = rstan::extract(fit1, permuted = TRUE)
#差のMCMCサンプルをデータフレーム形式に
diff1 = data.frame(diff = fit1data$diff)
#差の事後分布を可視化
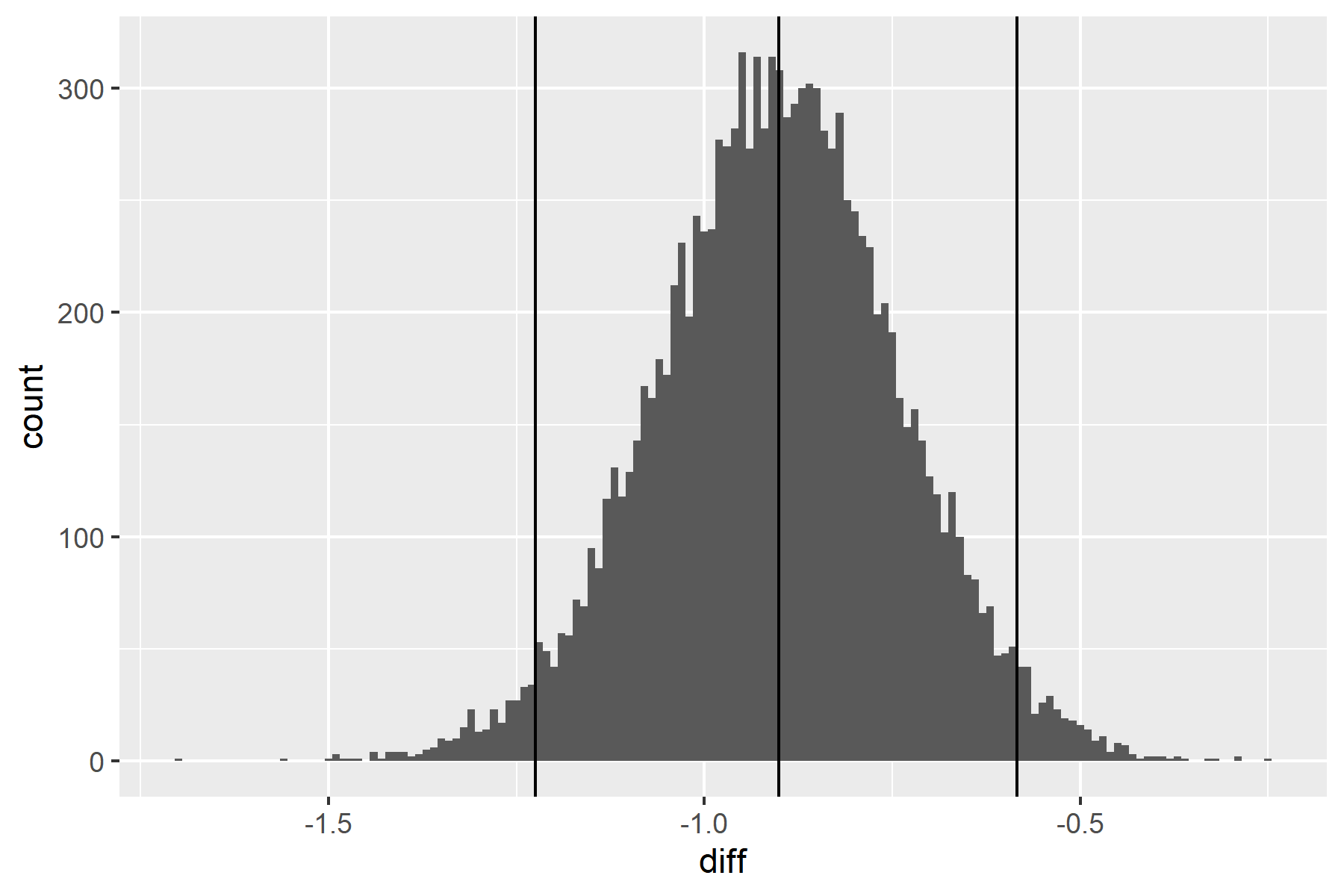
diff1 %>% 
    ggplot(aes(x = diff))+
    geom_histogram(binwidth = 0.01)+
    #95%確信区間と中央値
    geom_vline(xintercept = quantile(diff1s$diff,
                                     probs = c(0.025, 0.5, 0.975)
                                     )
               )

縦線は，事後分布の2.5%，50%，97.5%を示しています。
ちなみに，今回の模擬データは以下のように生成しました。

模擬データ

#乱数種固定
set.seed(108)
#模擬データの設定
##日本平均
mu1_j = 422/60
##差分
d1 = -1
#データ生成
sample1 = data.frame(time = rnorm(n = 20,
                                  mean = mu1_j+d1,
                                  sd = 1
                                  )
                     )

stanモデルのまんまです。
日本平均7.03時間から1時間短い，6.03時間を平均とした正規分布から生成しています。
差の真値-1に対し，推定結果は-0.9(確信区間-1.22, -0.58)ですから，まぁまぁ推定できているということがわかりますね。

ちなみに，Stanで遊ぶ最初の頃は模擬データを自分で生成して使うのが個人的には良いと思っています。
いろんな公開データを使うのも楽しいですが，自分で模擬データを生成すると，データの生成過程を意識できる点と，推定の精度が実感できる点でお勧めです。

対応のないt 検定

今度は，独立な・無関係な2つのデータの平均値の比較です。
ここでは，2つの部署間の睡眠時間の差を推定する場合を考えます。

模擬データ

今回は模擬データの生成から始めます。

模擬データ生成と可視化

#乱数種固定
set.seed(108)
#模擬データの設定
##部署Aの平均
mu2_a = 6.2
##部署Bの平均 
mu2_b = 7.7
##分散 今回は等分散と仮定
sd2 = 1
##データ数
n2_a = 100
n2_b = 90
#データ生成
sample2 = data.frame(id = c(1:(n2_a+n2_b)),
                     time = c(rnorm(n = n2_a,
                                    mean = mu2_a,
                                    sd = sd2
                                    ),
                              rnorm(n = n2_b,
                                    mean = mu2_b,
                                    sd = sd2)
                              ),
                     #部署変数
                     section = c(rep("A", n2_a), 
                                 rep("B", n2_b)
                                 )
                     )
#ヒストグラム
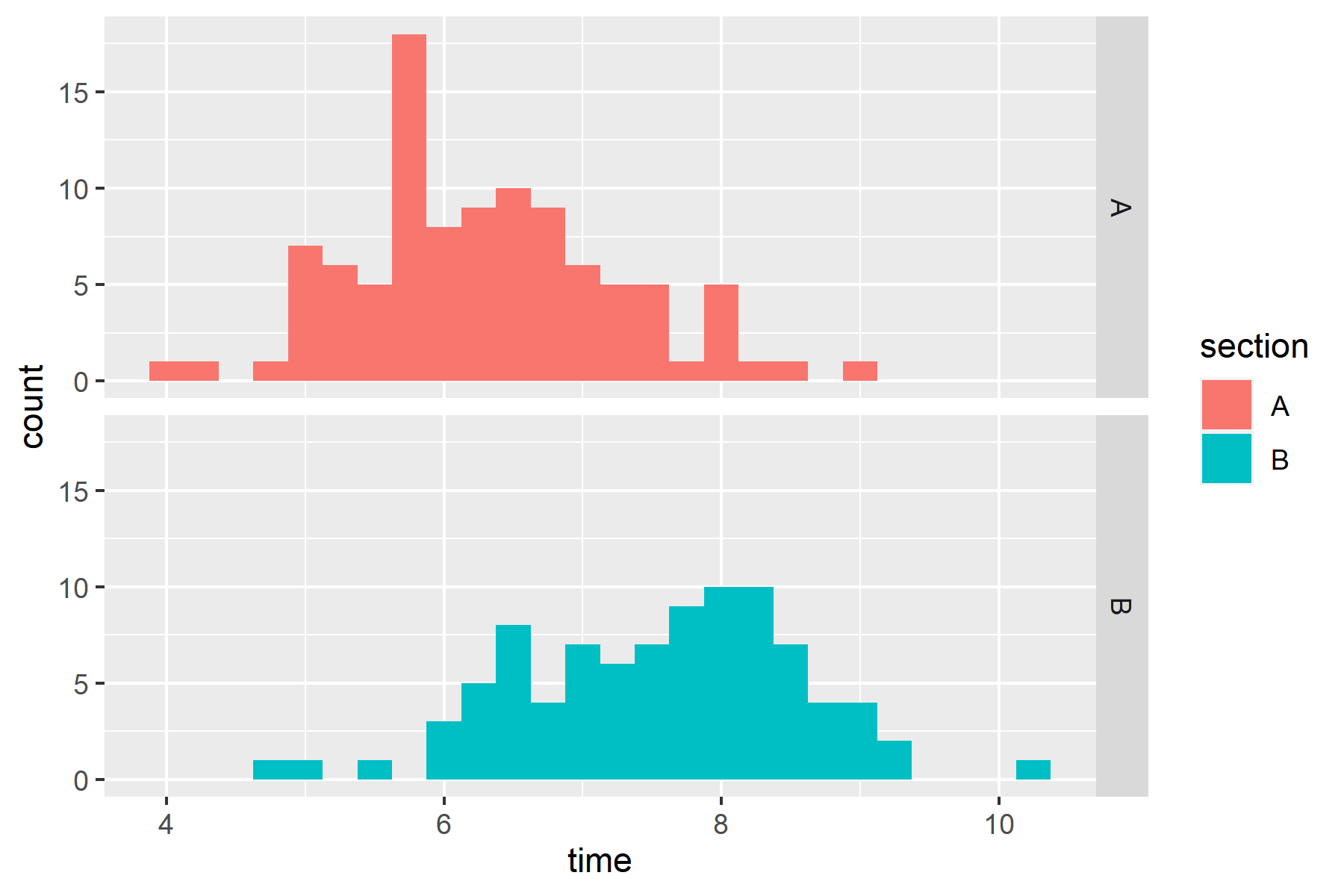
sample2 %>% 
    #色を部署ごとに指定
    ggplot(aes(x = time,
               fill = section)
               )+
    #ヒストグラムの描画と階級幅の指定
    geom_histogram(binwidth = 0.25)+
    #部署で図をわける
    facet_grid(section~.)

モデル

部署Aと部署Bの平均値の差をそのまま組み込みます。
部署Bの生成モデルは以下のとおり。

$Time_{部署B}[i] \sim Normal(mu_{部署A}+diff, sig)$

このままだと，部署Bの平均パラメタをMCMCサンプルから一々計算することになるので，以下のようにtransformed parametersで，$mu_{部署B}$を定義しています。

対応のないt検定stanモデル

data {
    int<lower = 0> N_a; //部署Aのデータ数
    int<lower = 0> N_b; //部署Bのデータ数
    real<lower = 0> Time_a[N_a]; //部署Aの睡眠時間
    real<lower = 0> Time_b[N_b]; //部署Bの睡眠時間
}

parameters {
    real<lower = 0, upper = 24> mu_a; //部署Aの平均
    real<lower = -24, upper = 24> diff; //部署間の差
    real<lower = 0> sig; //標準偏差，今回は等分散
}

transformed parameters {
    real mu_b; // 部署Bの平均
    mu_b = mu_a + diff; //部署Bの平均を部署Aと部署間の差で定義
}

model {
    //モデル
    //部署Aの社員さんの睡眠時間
    Time_a ~ normal(mu_a, sig);
    //部署Bの社員さんの睡眠時間
    Time_b ~ normal(mu_b, sig);
    //事前分布
    mu_a ~ normal(8, 12); //8時間+-24時間を意識した事前分布
    diff ~ normal(0, 12); //-24~24時間を意識した事前分布
    sig ~ cauchy(0, 5); //裾の広い事前分布
}

上記のモデルをmodel2.stanとして保存します。
ちなみに，異分散を仮定する場合には，$sig$を2種類用意してあげるだけでOKです。

推定

データ準備からMCMC

#Stan用のデータセット
data2 = list(N_a = sample2 %>%
                 dplyr::filter(section == "A") %>% 
                 nrow(), 
             N_b = sample2 %>%
                 dplyr::filter(section == "B") %>% 
                 nrow(),
             Time_a = sample2 %>% 
                 dplyr::filter(section == "A") %>% 
                 .$time,
             Time_b = sample2 %>%
                 dplyr::filter(section == "B") %>% 
                 .$time
             )
#モデルをコンパイル
model2 = stan_model(file = "model2.stan")
#MCMC
fit2 = sampling(model2,
                data = data2,
                chains = 4,
                iter = 4000,
                warmup = 1000
                )

推定結果

fit2の実行結果の一部

       mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
mu_a   6.14    0.00 0.09   5.96   6.08   6.14   6.21   6.33  6864    1
diff   1.46    0.00 0.14   1.19   1.36   1.46   1.55   1.73  6841    1
sig    0.94    0.00 0.05   0.85   0.90   0.93   0.97   1.04  7676    1
mu_b   7.60    0.00 0.10   7.40   7.53   7.60   7.67   7.79 12753    1

模擬データ生成時のパラメタをうまく推定できているようです(収束チェックは省略)。
ちなみに，差の95％確信区間は1.19 ~ 1.73で，部署Bのほうが少なく見積もっても1時間以上は長く寝ているようです。
コードは省略しますが，各平均パラメタの事後分布は以下のとおりで，平均パラメタの差も視覚的に確認ができます。

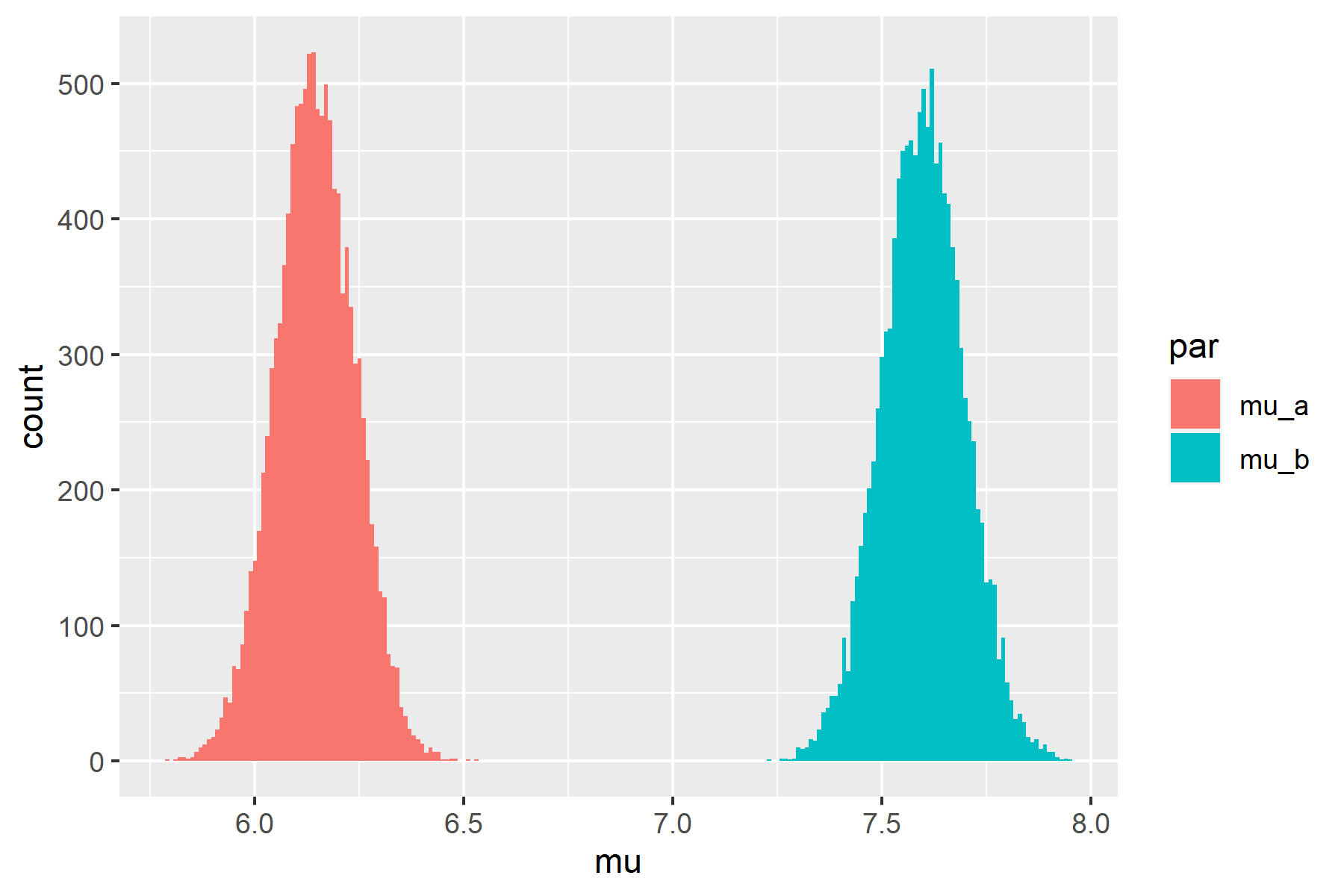
対応のあるt 検定

いよいよ最後(?)のt 検定です。
対応のあるt 検定は，要は相関のあるデータ間の平均値の差がターゲットなので，多変量正規分布からのデータ生成を仮定するということです。
ここでは，眠れないなぁという15人に超快眠法を教示する前後で睡眠時間が変わったか推定する場合を考えます。

模擬データ

今回も模擬データから準備します。
多変量正規分布からの乱数生成なので，MASSパッケージのmvrnormを用います。

模擬データ生成と可視化

#模擬データ生成
#乱数種固定
set.seed(108)
#模擬データの設定
##教示前の平均
mu3_pre = 5.5
##教示後の平均 
mu3_pos = 7
##分散
sd3 = 1
##共分散
cvar3 = 0.6
##データ数 
n3 = 15
#データ生成
##mvrnorm関数で使うための下準備
library(MASS)
mu3 = c(mu3_pre, mu3_pos)
cov3 = matrix(c(sd3, cvar3, cvar3, sd3),
              ncol = 2
              )
##生成
sample3 = mvrnorm(mu = mu3,
                  Sigma = cov3,
                  n = n3) %>% 
    #データフレーム化と，変数名変更
    data.frame() %>% 
    dplyr::rename("Pre" = X1, 
                  "Post" = X2)
#可視化
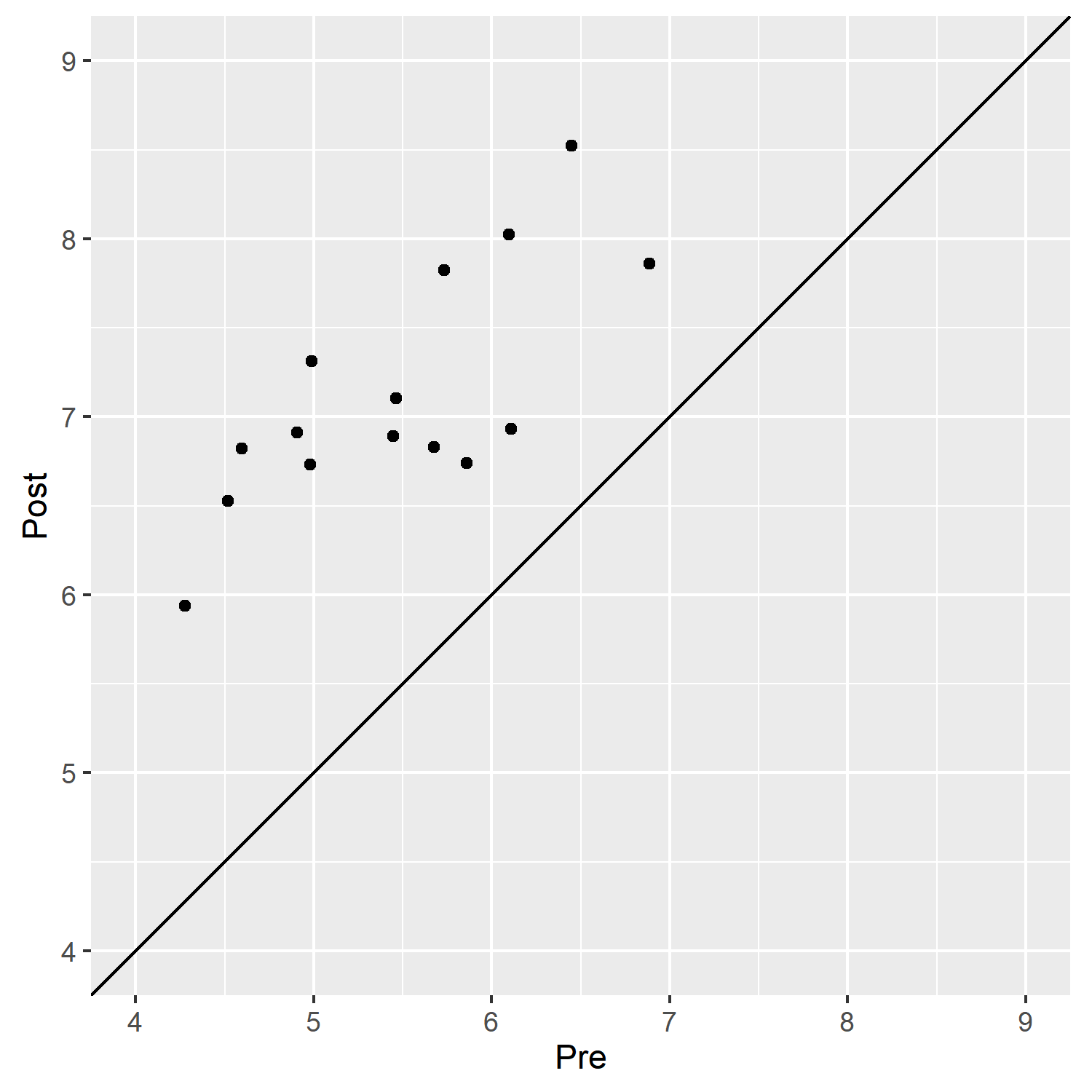
plotsample3 = sample3 %>% 
    ggplot(aes(x = Pre,
               y = Post)
           )+
    geom_abline(intercept = 0,
                slope = 1)+
    geom_point()+
    coord_equal(xlim = c(4, 9),
                ylim = c(4, 9)
                )

線分より下にプロットされていないので，15人全員の睡眠時間が伸びていたということですね。

モデル

多変量正規分布を扱うので，相関パラメタと共分散行列が必要になります。

対応のあるt検定stanモデル

data {
    int<lower = 0> N; //データ(調査人数)
    vector<lower = 0>[2] Time[N]; //事前と事後の睡眠時間
}

parameters {
    vector<lower = 0, upper = 24>[2] mu; //事前と事後の平均
    vector<lower = 0>[2] sig; //事前と事後の標準偏差，異分散想定
    real<lower = -1, upper = 1> r; //相関
}

transformed parameters {
    cov_matrix[2] cov; //2*2の分散共分散行列
    cov[1, 1] = sig[1]^2;
    cov[2, 2] = sig[2]^2;
    cov[1, 2] = sig[1] * sig[2] * r;
    cov[2, 1] = sig[1] * sig[2] * r;
}

model {
    //モデル
    Time ~ multi_normal(mu, cov);  //多変量正規分布
    //事前分布
    mu[1] ~ normal(8, 12); //8時間+-24時間を意識した事前分布
    mu[2] ~ normal(8, 12); //8時間+-24時間を意識した事前分布
    sig[1] ~ cauchy(0, 5); //裾の広い事前分布
    sig[2] ~ cauchy(0, 5); //裾の広い事前分布
    r ~ uniform(-1, 1); //無情報事前分布，パラメタ制約によりデフォルト通りのため記載は不要
}

generated quantities {
    //平均パラメタ間の差を生成
    real diff;
    diff = mu[2] - mu[1];
}

model3.stanとして保存してください。

推定

データ準備からMCMC

#データ準備
data3 = list(N = nrow(sample3),
             Time = cbind(sample3$Pre, sample3$Post)
             )
#モデルをコンパイル
model3 = stan_model(file = "model3.stan")
#MCMC
fit3 = sampling(model3,
                data = data3,
                chains = 4,
                iter = 4000,
                warmup = 1000
                )

推定結果

fit3の実行結果の一部

         mean se_mean   sd  2.5%   25%  50%  75% 97.5% n_eff Rhat
mu[1]    5.46    0.00 0.22  5.03  5.32 5.47 5.60  5.89  5232    1
mu[2]    7.13    0.00 0.19  6.75  7.01 7.13 7.25  7.51  5471    1
sig[1]   0.83    0.00 0.17  0.57  0.70 0.80 0.92  1.23  5829    1
sig[2]   0.73    0.00 0.15  0.50  0.62 0.71 0.81  1.10  5649    1
r        0.69    0.00 0.15  0.33  0.61 0.72 0.80  0.89  6719    1
diff     1.67    0.00 0.16  1.34  1.57 1.67 1.77  1.98 13333    1

概ね上手く推定できているようです。
しれっと異分散を仮定していますが，模擬データ自体は等分散を仮定したものです。ただ，現実的には等分散を積極的に仮定できるシーンはそう多くないと思うので，今回のモデルでは異分散としました。

ちなみに，
$Time_{Post}[i] \sim Normal(Time_{pre}[i]+diff, sig)$
という風にも考えられるのでは？という意見があるかもしれません。私も最初はそう考えたのですが，データ生成過程を意識すると，多変量正規分布を想定するほうが自然かなぁ，と。

Stanにおけるパラメタ制約について

修正前の記事では，modelブロック内の事前分布において一様分布を指定し，parametersブロックではその事前分布よりも広い範囲でしか制約を与えていませんでした・・・が，この方法は誤りです。申し訳ございません(;´Д｀)
具体的に説明していきます。

範囲の制約はparametersブロック

Stanは，パラメタが同時に成立する空間内からサンプリングしてくれる訳ですが，その範囲を指定・制約できるのはparametersブロックです。

なので，parametersブロックでの範囲指定よりも狭い範囲を事前分布で指定すると，「あれ，ここまで探したいのにないよ？」という感じで，サンプリング効率が悪くなります。そして，このことはStan公式マニュアルにしっかり明記してあります。

ちなみに，parametersブロックで範囲を設定した場合，Stanはその範囲を反映した一様分布を事前分布として自動的に設定してくれます。

• 例：real<lower = -24, upper = 24> diff;とすると，
  事前分布にdiff ~ uniform(-24, 24)が自動的に与えられる

もしこのデフォルト以外の事前分布を指定する場合には，以下の2つの方法があります。

• 弱情報事前分布：十分な幅をもった分布～例：$Normal(0, 1000)$
• 情報事前分布：完全には制約しないけど，特定区間に値が集中する分布～例：$Normal(0, 12)$

なお，今回は，全体を通して1日当たりの睡眠時間を例題としたので，平均パラメタには情報事前分布として正規分布(任意の平均から24時間以内に95％以上が集中)を指定しました。
(標準偏差パラメタには，弱情報事前分布である半Cauchy分布を指定しました。)

マニュアルをきちんと読むって大事です(自戒)。

最後に

…めちゃくちゃ長くなってしまいました。
最後のほうはぶっ飛ばしている感ありまくりなので，時間があるときに編集していこうかと思います。

t 検定に限らず，データ生成過程を意識することで，様々なモデルを考えることができます。色々なStanコードを知るたびに，世界が広がっていく感覚があって，すごく楽しいです。
アドカレの記事を写経するだけでなく，データを変えてみたり，モデルを一部いじってみたり，色々楽しんでみるとよりのめり込めると思います。

その一方で，あるモデルがどの程度妥当なのかを評価することは容易ではありません。単なるモデル指標比較だけでなく，他にどんなモデルが考えられるのか，自分のモデルで意識していない部分はどこなのか…，色々な観点からモデルを考えていくことが大事なんだろうな，と感じています。

ともあれ，今回のアドカレにはその参考になる記事ばかりです！
今までStanに馴染みがなかった方も，これを機にMCMCしてみましょう。

明日は，psycle44さんの記事で，テーマは項目反応理論です。


Enjoy!!

1. 差があるか否かを事後分布の95％確信区間によって言及することは慣例的になっている部分もあるかと思いますが，対象とする現象によって異なるのかな，と個人的には考えています。 ↩