この記事は,Stan Advent Calendar2020の第22日目の記事です。
N = 1だけど分析したい
世の中にはたくさんのデータがあって,分析する際にサンプルサイズを気にしないで済む,むしろ多すぎて困っているという状況もあるかもしれません。が・・・逆に,サンプルサイズが小さすぎてどうしよう,という状況もあると思います。
サンプルサイズが小さいと,rawデータをそのままグラフ等で示したり,記述統計量の記載だけで留まらずを得ない・・・となってしまいますよね。そこで,この記事ではN = 1の状況におけるモデリングを試みようと思います。
※当初全く違うネタの予定だったのですが,Rstudioが爆発しまくったため方向性をぐるりと変えました。薄い内容ですいませんOrz
想定事例
いきなりですが,何かしら衝撃的な刺激に対する生理反応を調べたいとします。
実験参加者は1人,刺激呈示後5秒間の心拍数平均が観測値です。(N = 1と言いつつ,観測値自体は複数あります。タイトル盛り過ぎました💦)
まず,バッファー刺激として黒点が呈示,その後一定間隔をおいて25個の刺激が順次呈示されます。25個の刺激のうち,5個の刺激は衝撃的な刺激で,他の20個はニュートラルな刺激となっています。
手元には,刺激の呈示順序,呈示刺激の種類,心拍数があり,このデータから衝撃的な刺激とニュートラルな刺激に対する心拍数の差異を明らかにしたいと思います。
模擬データの確認
模擬データはこんな感じです。
library(tidyverse)
# データ
data = data.frame(Id = c(rep(1, 26)),
M = c(1:26),
Tr = c(0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 0, 0),
Y = c(88.00000,
86.57216, 85.09881, 84.45053, 83.06194, 84.45066,
85.25173, 84.39252, 83.05577, 84.26889, 83.05517,
83.21877, 82.80680, 81.54350, 80.92468, 80.45817,
78.94766, 78.79618, 79.16357, 79.17745, 78.93255,
77.77406, 79.10931, 77.92719, 76.97891, 74.68802)
)
# 可視化
data %>%
mutate(LAG = Y - lag(Y),
Tr = as.factor(Tr)) %>%
ggplot(aes(x = M, y = Y))+
geom_vline(xintercept = if_else(data$Tr>0, data$M, NULL),
col = "gray",
lty = 2)+
geom_line(aes(group = Id), col = "darkgray")+
geom_point(aes(col = LAG,
pch = Tr),
size = 3)+
scale_color_gradient2(low = "blue",
high = "red",
mid = "yellow")+
theme_classic()
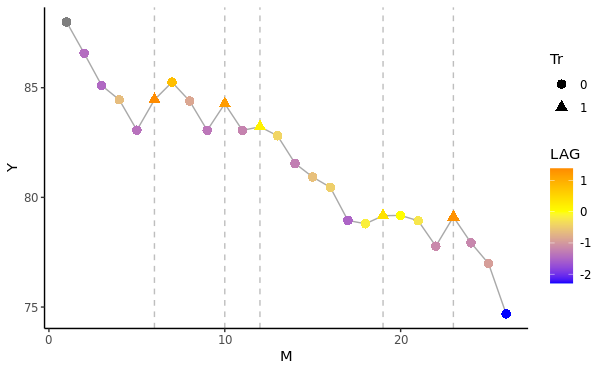
垂直点線(及び▲プロット)は衝撃的な刺激が呈示された時で,点の色は直前の値との差分値($Y_t-Y_{t-1}$)を示しています。ここでは,前の値より心拍数が高くなるほど赤色に近づくように指定しました。
どうやら,衝撃的な刺激が示されたときは心拍数が上がっているようです。また,時間経過に伴って心拍数は徐々に低下している様子も確認できます。
恐らく,こういったグラフに加えて,差分値を刺激別に示したり,差分値の代表値を示したり・・・というのが通常の流れだと思います。
モデリング
一番気になるのは,衝撃的な刺激によって心拍数に影響があるのかですが,時間経過の影響も見逃せません。
ここでは,以下のモデルを考えました。
$Y_t \sim Normal(Y_{t-1}+\delta+effect, sig)$
ある時点$t$の観測値$Y_t$は,1時点前の観測値$Y_{t-1}$に時間の影響$\delta$と刺激の効果$effect$が加わり,さらに誤差が加わって生成される,というモデルです。ちなみに,刺激の効果$effect$は衝撃的な刺激呈示時のみのパラメータです。
時間の影響を考えるときに,前の値に似ているだろうという仮定(1)と,前の値から一定程度減少しているだろうという仮定(2)の2つを置いています。
この仮定がどこまで自然なのかは難しいところですが,少なくとも仮定(1)は自己相関としてそこまで不自然ではないと思います(時系列モデルのランダムウォークモデルと同様です。)。仮定(2)については,時間経過による減少の程度をどう考えるか次第だと思います。今回は,序盤に急速な減少をする等とは仮定せずに,計測中ほぼ一貫して,同程度減少し続けるというモデルになっています。
また,衝撃的な刺激の効果についても常に一定であると仮定しています。
stanモデルは以下のとおり。
data {
int<lower=1> M; //計測時点
vector<lower=0, upper=1>[M] Tr; //刺激の種類
vector<lower=40, upper=150>[M] Y; //観測値
}
parameters {
real<lower=-20, upper=20> eff; //刺激の効果
real<lower=-20, upper=20> delta; //時間の影響
real<lower=0> sig;
}
model {
for (m in 2:M) {
Y[m] ~ normal(Y[m-1]+delta+(eff*Tr[m]), sig);
// Tr[m]が1のときだけeffが加わる
}
sig ~ cauchy(0, 5);
}
generated quantities {
vector[M] Y_pred; //予測
for ( m in 2:M ){
Y_pred[1] = Y[1];
Y_pred[m] = normal_rng(Y_pred[m-1]+delta+(eff*Tr[m]), sig);
}
}
generated quantitiesでパラメタの事後分布を利用して予測をしています。
上記モデルをmodel_N1.stanとして保存します。
推定
library(rstan)
## 魔法の呪文
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
# コンパイル
m = stan_model(file = "model_N1.stan")
# stanデータ
d = list(M = nrow(data), Y = data$Y, Tr = data$Tr)
# MCMCハァハァ
fit1 = sampling(m,
data = d,
chains = 4,
iter = 20000,
warmup = 10000,
thin = 10
)
そんなに時間はかからないはず。
推定結果
収束確認は(問題なかったので)飛ばして,主なパラメタのみ示していきます。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
eff 1.79 0.01 0.36 1.09 1.54 1.79 2.02 2.51 3854 1
delta -0.89 0.00 0.16 -1.21 -1.00 -0.89 -0.78 -0.57 3729 1
sig 0.71 0.00 0.11 0.53 0.63 0.70 0.77 0.96 4087 1
衝撃的な刺激が呈示されたときの心拍数の変化を示すeffは概ね1.79でした。95%確信区間の下限も1.09で,基本的に衝撃的な刺激が呈示されたときに心拍数は上昇していると考えてもよさそうです。
一方,時間経過による心拍数の変化deltaは-0.89で,95%確信区間の上限も負の値なので,やはり時間経過とともに心拍数が低下していると考えてもよさそうです。
しかしながら,実際これらのパラメタを利用して元のデータをどの程度予測できるのか気になりますよね。下の図をご覧くださいませ。
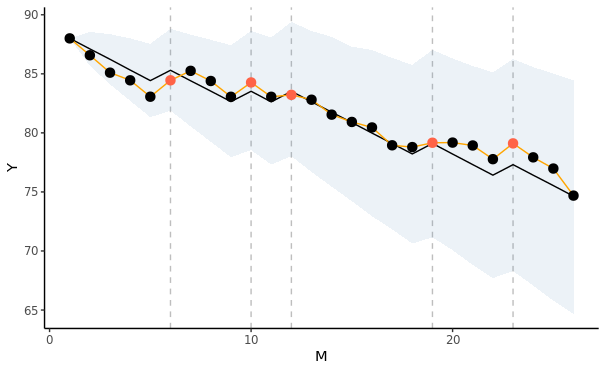
丸点プロットとオレンジ線が実際の観測値で,垂直点線と赤丸が衝撃的な刺激が呈示されたタイミングです。黒線が事後予測分布の平均,うっすら背景が事後予測分布の95%区間になります。
こんなに幅があるのか・・・と思ってしまいますが,そもそもデータが少ないので仕方ないと思います。一方,衝撃的な刺激が呈示されたときの95%区間は直前の値の区間よりも高い値になっています。
この結果をきちんと予測できたとみなせるかどうかは,この実験に対する背景知識次第だと思いますが,一応極端にはずれてはなさそうです(当然ながら,短時間画面を見ているだけで心拍数が20近くも減少するのか?等の疑問はあります。)。
まとめ
N = 1でも(盛り過ぎ),事前知識とモデリングによって,データからある程度情報を抽出できたのではないでしょうか。
ちなみに,時系列モデルでいえば状態空間モデルといった汎用性の高いモデルもありますが,過去のStanアドカレ記事(kosugittiさんの記事)にもあるように,時点数25程度ではうまくいかないことが多いです。
さて,私自身がサンプルサイズの小さいデータを対象にすることがとても多いので,極端な例をやってみました。サンプルサイズが小さくてもモデリングによって有用な情報を引き出せることもあると思いますので,今後も諦めずに日々頑張っていきたいと思います。
ただし,強い仮定を置かざるを得ないケースが多いと思うので,注意をしながら勉強&MCMCしていきたいとも思う今日この頃です。( ´-`)
最後に,予測図のコードを置いておきます。
他のパッケージを使わずに書いてはいるものの,美しさの欠片もありませんので,せめてクリスマス要素を・・・。
良いクリスマスと年末でありますように。
fit1 %>%
rstan::extract() %>%
data.frame() %>%
dplyr::mutate(sid = c(1:nrow(.))) %>%
dplyr::select(-eff, -delta, -sig, -lp__) %>%
tidyr::pivot_longer(-sid,
names_to = "M",
values_to = "Y_pred") %>%
dplyr::mutate(Ms = c(rep(1:26, 4000))) %>%
dplyr::group_by(Ms) %>%
dplyr::summarise(mean = mean(Y_pred),
Btm = quantile(Y_pred, 0.025),
Upr = quantile(Y_pred, 0.975)) %>%
dplyr::ungroup() %>%
ggplot(aes(x = Ms, y = mean))+
geom_vline(xintercept = if_else(data$Tr>0, data$M, NULL),
col = "gray",
lty = 2)+
geom_ribbon(aes(ymin = Btm, ymax = Upr),
fill = "steelblue", #緑にしたらもみの木に・・・
alpha = 0.1)+
geom_line()+
geom_line(data = data, aes(x = M, y = Y),
col = "orange")+
geom_point(data = data, aes(x = M, y = Y, col = as.factor(Tr)),
size = 3,
alpha = 1)+
#観測値をクリスマスカラーに
scale_color_manual(values = c("green", "tomato"))+
labs(y = "Y", x = "M")+
theme_classic()+
theme(legend.position = "none")