この記事はフロムスクラッチ Advent Calendar 2016の11日目の記事です。
最近はPythonでTensorFlowやChainerを使ってみることが流行っていますが、今回はあえてRのニューラルネットパッケージであるneuralnetを使ってみました。
公式リファレンスのneuralnet.pdfにあるサンプルコードを参考にします。
想定読者
- ニューラルネットを勉強をしたことがある人
- 統計学の勉強をしたことがある人
- Rを触ったことがある人
- Rでニューラルネットを使いたい人
準備
パッケージをインストールします。
> install.packages("neuralnet")
> library("neuralnet")
XOR問題
単純パーセプトロンでは学習できない、XORの学習をします。
まずは、データの準備。
> XOR <- c(0,1,1,0)
> xor.data <- data.frame(expand.grid(c(0,1), c(0,1)), XOR)
xor.dataはこのようになっています。
> xor.data
Var1 Var2 XOR
1 0 0 0
2 1 0 1
3 0 1 1
4 1 1 0
そして、ニューラルネットを構築します。
net.xor <- neuralnet(XOR~Var1+Var2, xor.data, hidden=4, rep=5)
第1引数はモデル、第2引数は訓練データです。また、hiddenでは隠れニューロンの数を指定し、repは訓練の回数を指定します。
(リファレンスでは隠れニューロンを2としていましたが、学習の精度が低かったので4にしています。)
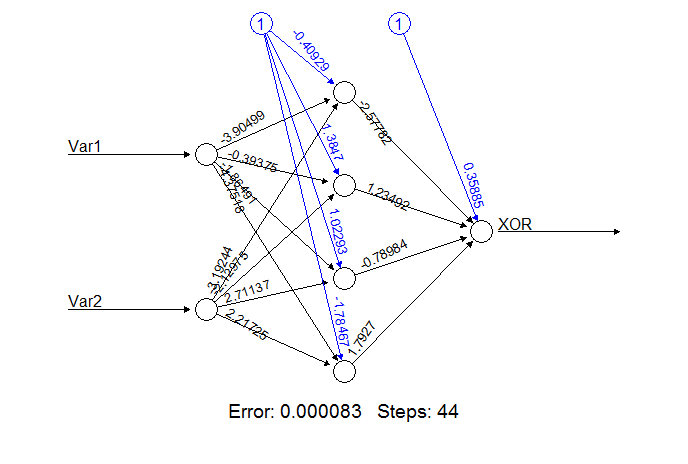
ネットワークとしてはこのようになります。
> plot(net.xor, rep="best")
rep="best"によって誤差が最も小さかったものをプロットしています。
net.xorが正しくXORを表すことを確認します。
> xor.data[-3]
Var1 Var2
1 0 0
2 1 0
3 0 1
4 1 1
> compute(net.xor, xor.data[-3])$net.result
[,1]
[1,] -0.005591322981
[2,] 0.991365312571
[3,] 1.003765769383
[4,] 0.006757999021
4つの入力に対して、それぞれ概ね正しい答えが得られました。
不妊データのロジスティック回帰
次は不妊に関するデータを扱います。
(センシティブなデータですが、リファレンスで使っていたので。。)
> data(infert, package="datasets")
> infert
education age parity induced case spontaneous stratum pooled.stratum
1 0-5yrs 26 6 1 1 2 1 3
2 0-5yrs 42 1 1 1 0 2 1
3 0-5yrs 39 6 2 1 0 3 4
4 0-5yrs 34 4 2 1 0 4 2
5 6-11yrs 35 3 1 1 1 5 32
6 6-11yrs 36 4 2 1 1 6 36
7 6-11yrs 23 1 0 1 0 7 6
8 6-11yrs 32 2 0 1 0 8 22
9 6-11yrs 21 1 0 1 1 9 5
10 6-11yrs 28 2 0 1 0 10 19
11 6-11yrs 29 2 1 1 0 11 20
12 6-11yrs 37 4 2 1 1 12 37
13 6-11yrs 31 1 1 1 0 13 9
14 6-11yrs 29 3 2 1 0 14 29
15 6-11yrs 31 2 1 1 1 15 21
16 6-11yrs 27 2 2 1 0 16 18
17 6-11yrs 30 5 2 1 1 17 38
18 6-11yrs 26 1 0 1 1 18 7
19 6-11yrs 25 3 2 1 1 19 28
20 6-11yrs 44 1 0 1 1 20 17
...(省略)
[ reached getOption("max.print") -- omitted 123 rows ]
データの説明はこちらをご参照ください。
自然・人工流産後の不妊症についてのデータです。
ネットワークを構築します。
net.infert <- neuralnet(case~parity+induced+spontaneous, infert, err.fct="ce", linear.output=FALSE, likelihood=TRUE)
被験者か対照群かを表すcaseを目的変数とし、parity(実験回数?)、induced(人工流産)、spontaneous(自然流産)を説明変数(共変量)としたモデルです。
err.fctは誤差関数を指定します。ceの場合はクロスエントロピーで、sseの場合は二乗誤差となります。デフォルトでは二乗誤差です。
linear.outputはact.fctを出力層のニューロンに適用しない場合はTRUEに、適用する場合はFALSEにします。
act.fctは活性化関数を指定します。デフォルトではロジスティック関数となります。
likelihoodがTRUEのとき、誤差関数が負の対数尤度と同等となる場合に情報量規準のAICとBICが計算されます。
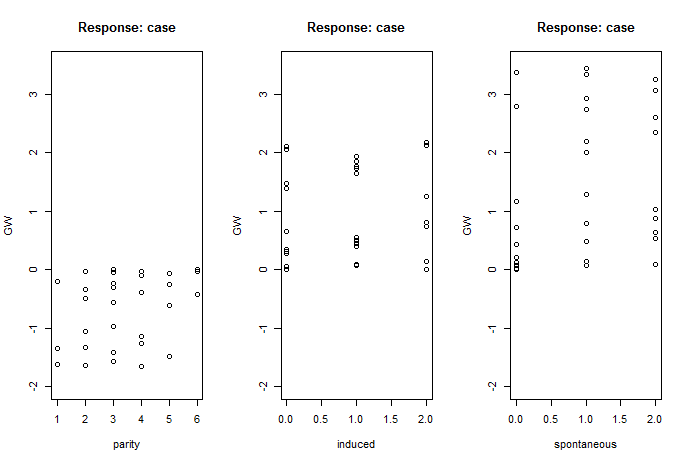
次にgwplotで各共変量の目的変数に対するGeneralized Weightをプロットします。
> par(mfrow = c(1,3))
> gwplot(net.infert, selected.covariate="parity", max=3.5, min=-2)
> gwplot(net.infert, selected.covariate="parity", max=3.5, min=-2)
> gwplot(net.infert, selected.covariate="induced", max=3.5, min=-2)
> gwplot(net.infert, selected.covariate="spontaneous", max=3.5, min=-2)
Generalized Weightは共変量の目的変数への影響度を表しています。0付近に集まる場合は余り影響を与えないことを表します。
spontaneousは他と比較すると影響度が大きいのかもしれません。
最後にconfidence.intervalでGeneralized Weightの信頼区間とNICを計算します。
confidence.interval(net.infert)
$lower.ci
$lower.ci[[1]]
$lower.ci[[1]][[1]]
[,1]
[1,] 0.2378732931
[2,] -0.7767930421
[3,] -5.6821658449
[4,] -8.7671639096
$lower.ci[[1]][[2]]
[,1]
[1,] -0.7548627922
[2,] -6.4897821363
$upper.ci
$upper.ci[[1]]
$upper.ci[[1]][[1]]
[,1]
[1,] 2.8480852032
[2,] 4.5389670051
[3,] 0.7944060804
[4,] 1.0157270261
$upper.ci[[1]][[2]]
[,1]
[1,] 4.3246718745
[2,] -0.7591746629
$nic
[1] 135.6941297
次にやりたいこと
Rのニューラルネットパッケージは他にも「nnet」というものがあるので、次はそれを触ってみようかと思います。
参考