『一休.com Advent Calendar 2024』の18日目の投稿です。
RESZAIKO 事業部エンジニアの所澤です。
『競プロが仕事の役に立つか?』がしばしばインターネットで話題になります。
深遠なテーマなので詳細には立ち入りませんが、競プロの経験を活かして現実の問題を解決できたので、そのエピソードをご紹介します。実例を通して競プロ知識の役立て方のヒントをお伝えできれば嬉しいです。
(ちなみに私自身は AtCoder を少しやったことがあるものの、全然コンテストに出れていない茶色コーダーです。どうぞお手柔らかに ![]() )
)
何が起きていたのか?
RESZAIKO はレストラン向けの業務支援 SaaS です。
RESZAIKO ではいくつかのプロダクト群を提供していますが、今回取り上げるのは予約と空席を管理するサービスです。
問題はオーバーブッキングを判定する処理で起きました。
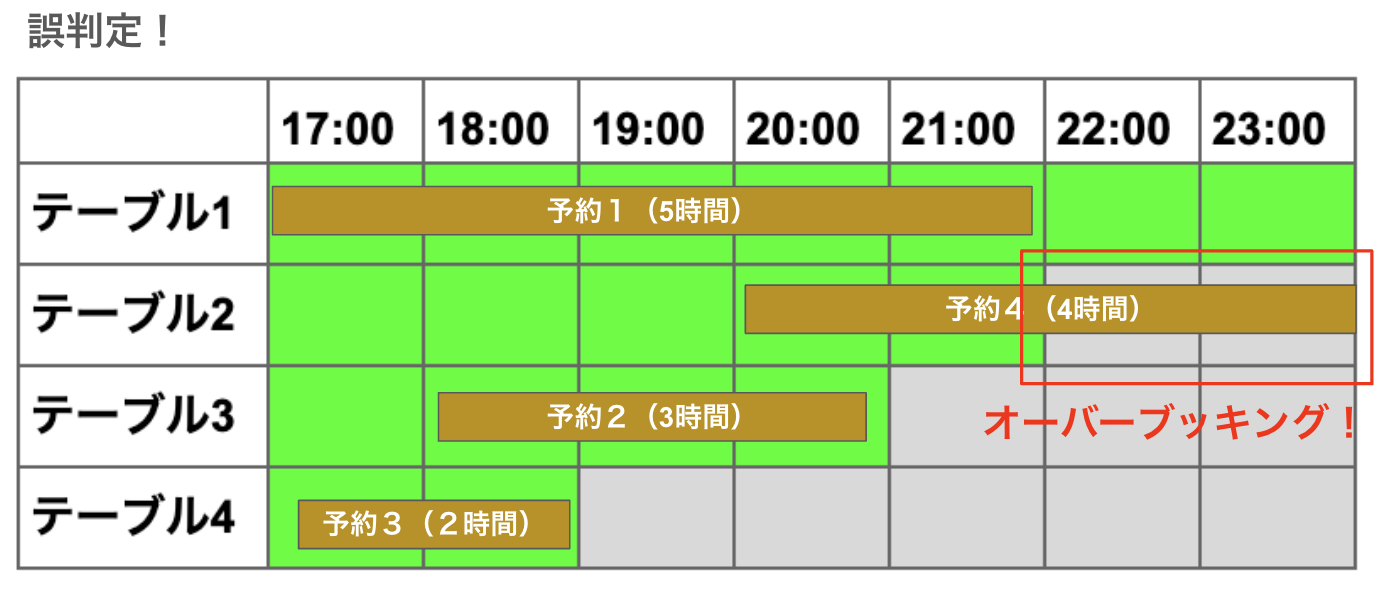
オーバーブッキングとは空いている席以上に予約が入ってしまっている状態です。例えば下の図はテーブル2の19:00以降は席が空いていないので...予約2はオーバーブッキングだと判定します。
このオーバーブッキングの判定が正しく行われておらず、実際はオーバーブッキングでないのにオーバーブッキングと判定してしまっていました。
どんな実装になっていたのか?
もともとは席を空席の時間が多い順、予約の長さが長い順にソートし予約を配置し、受付不可の時間に予約が入っていないかチェックしていくという単純な実装でした。
このロジックはわかりやすいですが、常に正解を出しはてくれません。例えば以下のケースで誤判定が発生します。
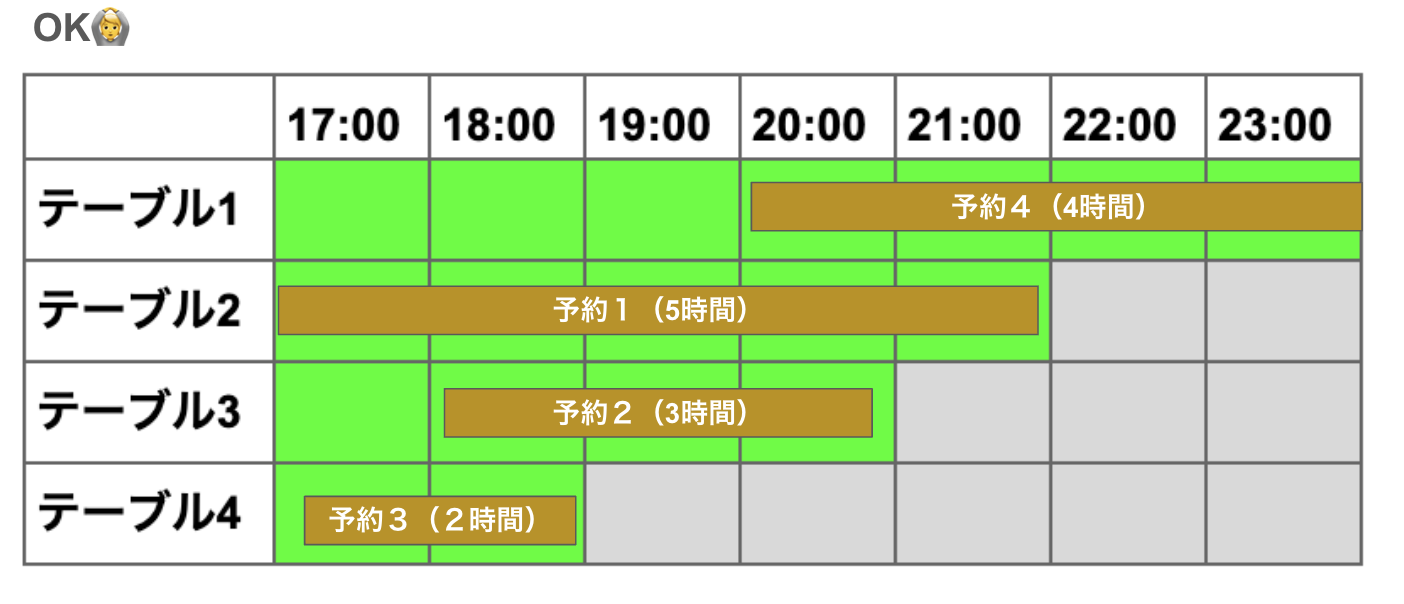
予約4,1,2,3 の順で並べれば空席に予約が入り切りますが、予約が長い順にソートすると予約1,4,2,1の順になり、オーバーブッキングと判定されてしまいます。
解決方法
どうすれば改善できるでしょうか?
STEP1: 全探索(全列挙)できるか検討する
まず思いつくのは考えうる予約の配置をすべてチェックすることです。単純ですがこれもれっきとしたアルゴリズムで、全探索(全列挙)と呼ばれます。
AtCoder の初級者向けのコンテストの序盤で出題されることも多く、基本のキとも言える典型アルゴリズムです。
席と予約の組み合わせを全列挙するためには、例えば席の並び順を固定して予約の全順列を考えれば良いです。
Python であれば itertools.permutations を使えばすべての並び順を列挙できます。
>>> from itertools import permutations
>>> list(permutations({'a', 'b', 'c'}))
[('b', 'a', 'c'), ('b', 'c', 'a'), ('a', 'b', 'c'), ('a', 'c', 'b'), ('c', 'b', 'a'), ('c', 'a', 'b')]
STEP2: 計算量を見積もる
これで解決! ではありません。計算量を見積もる必要があります。
全順列なので考えられる予約の並び順はの N! 通りです。
予約が10個なら 10! = 3,628,800,20 通り、20個あったときは 20! = 2,432,902,008,176,640,000通りとなります。
さらに予約と席のそれぞれについてオーバーブッキングしていないかチェックする必要があるので計算量は N * N! です。
アプリケーションで扱う席数は最大で N = 100程度ですが...現実的な時間で組み合わせをチェックできるでしょうか?
結論、ぜんぜん間に合いません。
数秒のうちに処理できる計算は Python で ~ 数百万、Rust や C++ でも数千万程度です。こういった計算量の肌感覚は競プロをはじめてすぐに誰しもが身につけるものです。
STEP3: 典型問題に落とし込む
どうやら別のアルゴリズムを考えなければいけなそうです。
まずは問題の構造を整理します。
ゴールはアプリケーション固有の問題を典型問題に帰着させること。「一般的な問題であれば誰かが良い解法(アルゴリズム)を思い付いているだろう」と考えます。典型的な問題に帰着できれば自分で解法を考えずにすみます。
一見してわかることは今回解きたい問題が「最適化問題」であることです
予約と席の組み合わせごとにオーバーブッキングしている時間幅(0 ~ 席の営業時間)が設定されていて、この時間の合計をなるべく0に近くなるような最適な組み合わせ探しています。
さらに問題から予約、席、オーバーブッキングといったドメインの情報を取り除いていきます。
以下のように整理ができました。
「それぞれN個の要素を持つ集合SとRがあり、Sの要素とRの要素のペアそれぞれに非負の値が設定されています。この値の合計値が最小になる組み合わせを求めてください」
なんだか一般的な問題になりましたね。
STEP4: アルゴリズムを適用する・実装する
STEP3 で一般化した問題を解く方法を考えます。自力で思いつけばかっこいいのですが...残念ながら自分の引き出しに良いアルゴリズムはありませんでした。
「一般的な問題であれば誰かが良い解法(アルゴリズム)を思い付いているだろう」
大事なことなのでもう一度書きますが、だれかが良いアルゴリズムを知っているはずなので調べていきます。競プロの練習をする中で「マッチングアルゴリズム」という単語を聞いたことがあったので、「マッチング アルゴリズム 最適化」などと検索して、この問題が「割り当て問題」という典型問題であることがわかりました。
割り当て問題の解法として「ハンガリアン法」などがあります。
ChatGPT に聞いてしまってもいいでしょう。
ハルシネーションが起きているかどうかは提案されたアルゴリズム名で検索をかけたり、書籍を参照して確かめればよいです。ハンガリアン法は『アルゴリズムイントロダクション第4版 第2巻』に詳しい解説が載っていました。
このアルゴリズムは N^3 で最適な組み合わせを計算することができるので、これで良さそうです。
今回対象のアプリケーションはたまたま Python で実装されていたので、scipy.optimize モジュール linear_sum_assignment を使うことで解決することができました。
よく使われるアルゴリズムであれば自前で実装せずともサードパーティの定番ライブラリがあったりします。(Scipy の linear_sum_assignment も元々はハンガリアン法で実装されていたのを後で効率的なアルゴリズムに変更したようです)
まとめ
現実の問題を典型問題に帰着して解決した様子をお話ししました。
私が関わっているWebアプリケーションの開発において、こういったアルゴリズムの知識が必要とされるのは全仕事の1%以下ですが、それでも競プロで培われる "計算量の肌感覚" や "問題の抽象化して構造を捉える力" は十分役に立つと感じています。